Aufgaben:Aufgabe 1.4Z: Alles rechteckförmig: Unterschied zwischen den Versionen
Aus LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} Datei:P_ID834__LZI_Z_1_4.png |right|Periodisches Rechtecksignal…“) |
|||
| (20 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} | ||
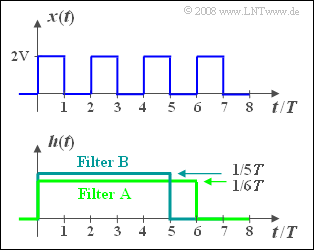
| − | [[Datei:P_ID834__LZI_Z_1_4.png |right|Periodisches Rechtecksignal und | + | [[Datei:P_ID834__LZI_Z_1_4.png |right|frame|Periodisches Rechtecksignal und <br>Filter mit rechteckförmiger Impulsantwort]] |
| − | Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist | + | Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist. |
| − | + | *Dieses Signal besitzt Spektralanteile bei der Grundfrequenz $f_0 = 1/T_0 = 1/(2T)$ und allen ungeradzahligen Vielfachen davon, das heißt bei $3f_0$, $5f_0,$ usw. Zusätzlich gibt es einen Gleichanteil. | |
| − | '' | + | *Dazu betrachten wir zwei Filter $\rm A$ und $\rm B$ mit jeweils rechteckförmiger Impulsantwort $h_{\rm A}(t)$ mit der Dauer $6T$ bzw. $h_{\rm B}(t)$ mit der Dauer $5T$. |
| + | *Die Höhen der beiden Impulsantworten sind so gewählt, dass die Flächen der Rechtecke jeweils $1$ ergeben. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Systembeschreibung im Zeitbereich]] | ||
| + | * Informationen zur Faltung finden Sie im Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]] im Buch „Signaldarstellung”. | ||
| + | *Wir verweisen Sie auch auf das interaktive Applet [[Applets:Zur_Verdeutlichung_der_grafischen_Faltung|Zur Verdeutlichung der graphischen Faltung]]. | ||
| + | |||
| + | |||
| Zeile 13: | Zeile 27: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Berechnen Sie das Ausgangssignal $y_{\rm A}(t)$ von Filter $\rm A$, insbesondere die Werte bei $t = 0$ und $t = T$. |
| − | |type=" | + | |type="{}"} |
| − | + | $y_{\rm A}(t = 0) \ =\ $ { 1 3% } $\rm V$ | |
| − | + | $y_{\rm A}(t = T) \ =\ $ { 1 3% } $\rm V$ | |
| + | |||
| + | |||
| + | {Geben Sie die Betragsfunktion $|H_{\rm A}(f)|$ an. Welcher Wert ergibt sich bei der Frequenz $f = f_0$? <br>Interpretieren Sie das Ergebnis der Teilaufgabe '''(1)'''. | ||
| + | |type="{}"} | ||
| + | $|H_{\rm A}(f = f_0)| \ =\ $ { 0. } | ||
| − | { | + | {Berechnen Sie das Ausgangssignal $y_{\rm B}(t)$ von Filter $\rm B$, insbesondere die Werte bei $t = 0$ und $t = T$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $y_{\rm B}(t = 0) \ =\ $ { 0.8 3% } $\rm V$ |
| + | $y_{\rm B}(t = T) \ =\ $ { 1.2 3% } $\rm V$ | ||
| + | {Wie lautet die Betragsfunktion $|H_{\rm B}(f)|$, insbesondere bei den Frequenzen $f = f_0$ und $f = 3 · f_0$? <br>Interpretieren Sie damit das Ergebnis der Teilaufgabe '''(3)'''. | ||
| + | |type="{}"} | ||
| + | $|H_{\rm B}(f = f_0)| \ =\ $ { 0.127 5% } | ||
| + | $|H_{\rm B}(f = 3f_0)| \ =\ $ { 0.042 5% } | ||
</quiz> | </quiz> | ||
| Zeile 29: | Zeile 53: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Das Ausgangssignal ist das Ergebnis der Faltungsoperation zwischen $x(t)$ und $h_{\rm A}(t)$: |
| − | '''2 | + | :$$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ |
| − | '''3 | + | *Aufgrund der Rechteckfunktion und der Dauer $6T$ kann hierfür auch geschrieben werden: |
| − | ''' | + | :$$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$ |
| − | + | *Man erkennt, dass diese Gleichung für alle $t$ das gleiche Ergebnis $y_{\rm A}(t) \rm \underline{\: = 1V}$ liefert. | |
| − | ''' | + | |
| − | + | ||
| + | |||
| + | '''(2)''' Der Betragsfrequenzgang lautet $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$ Dieser weist Nullstellen im Abstand $1/(6T)$ auf. | ||
| + | *Somit liegen auch bei $f_0$, $3f_0$, $5f_0$ usw. jeweils Nullstellen vor. | ||
| + | *Insbesondere gilt auch $|H_{\rm A}(f = f_0)| \underline{\: = 0}$. | ||
| + | *Vom Spektrum $X(f)$ bleibt somit nur der Gleichanteil $1 \hspace{0.05cm} \rm V$ unverändert erhalten. | ||
| + | *Dagegen sind alle anderen Spektrallinien in $Y_{\rm A}(f)$ nicht mehr enthalten. | ||
| + | |||
| + | |||
| + | [[Datei:P_ID836__LZI_Z_1_4_c.png | Grafische Verdeutlichung der Faltungsoperation| rechts|frame]] | ||
| + | '''(3)''' Analog zur Teilaufgabe '''(1)''' kann man hier für das Ausgangssignal schreiben: | ||
| + | :$$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$ | ||
| + | *Es ergibt sich ein um den Mittelwert $1 \ \rm V$ schwankender dreieckförmiger Verlauf ⇒ siehe untere Grafik. | ||
| + | *Da jeweils zwei Rechtecke und drei Lücken ins Integrationsintervall fallen, gilt für $t = 0, t = 2T,$ usw.: | ||
| + | :$$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$ | ||
| + | *Bei $t = T,\ 3T, \ 5T, $ usw. sind jeweils drei Rechtecke und zwei Lücken zu berücksichtigen: Man erhält: | ||
| + | :$$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Die Betragsfunktion lautet nun allgemein bzw. bei den Frequenzen $f = f_0 = 1/(2T)$ und $f = 3f_0$: | ||
| + | :$$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$ | ||
| + | |||
| + | Interpretation: | ||
| + | *Die Spektralanteile des Rechtecksignals bei $f_0, 3f_0,$ usw. werden zwar nun nicht mehr unterdrückt, aber mit steigender Frequenz immer mehr abgeschwächt und zwar in der Form, dass der Rechteckverlauf in ein periodisches Dreiecksignal gewandelt wird. Der Gleichanteil $(1 \hspace{0.05cm} \rm V)$ bleibt auch hier unverändert. | ||
| + | *Beide Filter liefern also den Mittelwert des Eingangssignals. Beim vorliegenden Signal $x(t)$ ist für die Bestimmung des Mittelwertes das Filter $\rm A$ besser geeignet als das Filter $\rm B$, da bei Ersterem die Länge der Impulsantwort ein Vielfaches der Periodendauer $T_0 = 2T$ ist. | ||
| + | *Ist diese Bedingung – wie beim Filter $\rm B$ – nicht erfüllt, so überlagert sich dem Mittelwert noch ein (in diesem Beispiel dreieckförmiges) Fehlersignal. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^ | + | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^1.2 Systembeschreibung im Zeitbereich^]] |
Aktuelle Version vom 18. Oktober 2019, 14:58 Uhr
Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist.
- Dieses Signal besitzt Spektralanteile bei der Grundfrequenz $f_0 = 1/T_0 = 1/(2T)$ und allen ungeradzahligen Vielfachen davon, das heißt bei $3f_0$, $5f_0,$ usw. Zusätzlich gibt es einen Gleichanteil.
- Dazu betrachten wir zwei Filter $\rm A$ und $\rm B$ mit jeweils rechteckförmiger Impulsantwort $h_{\rm A}(t)$ mit der Dauer $6T$ bzw. $h_{\rm B}(t)$ mit der Dauer $5T$.
- Die Höhen der beiden Impulsantworten sind so gewählt, dass die Flächen der Rechtecke jeweils $1$ ergeben.
Hinweise:
- Die Aufgabe gehört zum Kapitel Systembeschreibung im Zeitbereich
- Informationen zur Faltung finden Sie im Kapitel Faltungssatz und Faltungsoperation im Buch „Signaldarstellung”.
- Wir verweisen Sie auch auf das interaktive Applet Zur Verdeutlichung der graphischen Faltung.
Fragebogen
Musterlösung
(1) Das Ausgangssignal ist das Ergebnis der Faltungsoperation zwischen $x(t)$ und $h_{\rm A}(t)$:
- $$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- Aufgrund der Rechteckfunktion und der Dauer $6T$ kann hierfür auch geschrieben werden:
- $$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$
- Man erkennt, dass diese Gleichung für alle $t$ das gleiche Ergebnis $y_{\rm A}(t) \rm \underline{\: = 1V}$ liefert.
(2) Der Betragsfrequenzgang lautet $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$ Dieser weist Nullstellen im Abstand $1/(6T)$ auf.
- Somit liegen auch bei $f_0$, $3f_0$, $5f_0$ usw. jeweils Nullstellen vor.
- Insbesondere gilt auch $|H_{\rm A}(f = f_0)| \underline{\: = 0}$.
- Vom Spektrum $X(f)$ bleibt somit nur der Gleichanteil $1 \hspace{0.05cm} \rm V$ unverändert erhalten.
- Dagegen sind alle anderen Spektrallinien in $Y_{\rm A}(f)$ nicht mehr enthalten.
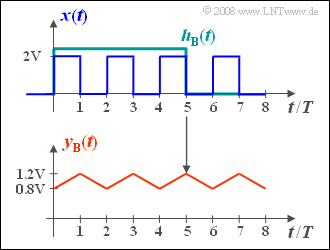
(3) Analog zur Teilaufgabe (1) kann man hier für das Ausgangssignal schreiben:
- $$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$
- Es ergibt sich ein um den Mittelwert $1 \ \rm V$ schwankender dreieckförmiger Verlauf ⇒ siehe untere Grafik.
- Da jeweils zwei Rechtecke und drei Lücken ins Integrationsintervall fallen, gilt für $t = 0, t = 2T,$ usw.:
- $$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$
- Bei $t = T,\ 3T, \ 5T, $ usw. sind jeweils drei Rechtecke und zwei Lücken zu berücksichtigen: Man erhält:
- $$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$
(4) Die Betragsfunktion lautet nun allgemein bzw. bei den Frequenzen $f = f_0 = 1/(2T)$ und $f = 3f_0$:
- $$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$
Interpretation:
- Die Spektralanteile des Rechtecksignals bei $f_0, 3f_0,$ usw. werden zwar nun nicht mehr unterdrückt, aber mit steigender Frequenz immer mehr abgeschwächt und zwar in der Form, dass der Rechteckverlauf in ein periodisches Dreiecksignal gewandelt wird. Der Gleichanteil $(1 \hspace{0.05cm} \rm V)$ bleibt auch hier unverändert.
- Beide Filter liefern also den Mittelwert des Eingangssignals. Beim vorliegenden Signal $x(t)$ ist für die Bestimmung des Mittelwertes das Filter $\rm A$ besser geeignet als das Filter $\rm B$, da bei Ersterem die Länge der Impulsantwort ein Vielfaches der Periodendauer $T_0 = 2T$ ist.
- Ist diese Bedingung – wie beim Filter $\rm B$ – nicht erfüllt, so überlagert sich dem Mittelwert noch ein (in diesem Beispiel dreieckförmiges) Fehlersignal.