Aufgaben:Aufgabe 1.3Z: Schwellenwertoptimierung: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
[[Datei:P_ID1268__Dig_Z_1_3.png|right]] | [[Datei:P_ID1268__Dig_Z_1_3.png|right]] | ||
In dieser Aufgabe wird ein bipolares Binärsystem mit AWGN–Rauschen („Additive White Gaussian Noise”) betrachtet, so dass für die Bitfehlerwahrscheinlichkeit | In dieser Aufgabe wird ein bipolares Binärsystem mit AWGN–Rauschen („Additive White Gaussian Noise”) betrachtet, so dass für die Bitfehlerwahrscheinlichkeit | ||
| − | $$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= \frac | + | $$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= \frac{1}{2} \cdot {\rm erfc} \left( \frac{s_0}{\sqrt{2} \cdot \sigma_d}\right) \hspace{0.05cm}$$ |
gilt. Hierbei sind folgende Funktionen verwendet: | gilt. Hierbei sind folgende Funktionen verwendet: | ||
$$\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | $$\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | ||
| Zeile 14: | Zeile 14: | ||
\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | Die obige Gleichung gilt für den Schwellenwert <i>E</i> = 0 unabhängig von den Symbolwahrscheinlichkeiten <i>p</i><sub>L</sub> und <i>p</i><sub>H</sub>. | ||
| + | Allerdings kann mit einem anderen Schwellenwert <i>E</i> eine kleinere Fehlerwahrscheinlichkeit erzielt werden, wenn die beiden Auftrittswahrscheinlichkeiten unterschiedlich sind (<i>p</i><sub>L</sub> ≠ <i>p</i><sub>H</sub>) | ||
| + | Die Streuung des Rauschanteils ist stets <i>σ<sub>d</sub></i> = 0.5 V, die beiden Amplituden des Detektionsnutzanteils sind mit ±1 V fest vorgegeben. Zu untersuchen sind folgende Symbolwahrscheinlichkeiten: | ||
| + | *<i>p</i><sub>L</sub> = 0.88 und <i>p</i><sub>H</sub> = 0.12, | ||
| + | *<i>p</i><sub>L</sub> = 0.31 und <i>p</i><sub>H</sub> = 0.69. | ||
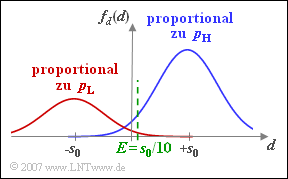
| + | In der Grafik ist dieser letzte Parametersatz und der Schwellenwert <i>E</i> = 0.1 · <i>s</i><sub>0</sub> dargestellt. | ||
| + | |||
| + | <b>Hinweis:</b> Die Aufgabe bezieht sich auf das [[ Kapitel1.2.]] Für die Ableitung der Q–Funktion gilt: | ||
| + | $$\frac{{\rm d\hspace{0.05cm}Q} (\it x)} {{\rm d}\hspace{0.05cm}x} = \frac{\rm 1}{\sqrt{\rm 2\pi}} | ||
| + | \cdot \rm e^{\it -x^{\rm 2}/\rm 2} \hspace{0.05cm}.$$ | ||
| + | Die Werte der Funktion Q(x) können Sie mit folgendem Interaktionsmodul bestimmen: | ||
| + | |||
| + | [[Komplementäre Gaußsche Fehlerfunktionen]] | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 24. Oktober 2017, 19:30 Uhr
In dieser Aufgabe wird ein bipolares Binärsystem mit AWGN–Rauschen („Additive White Gaussian Noise”) betrachtet, so dass für die Bitfehlerwahrscheinlichkeit $$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= \frac{1}{2} \cdot {\rm erfc} \left( \frac{s_0}{\sqrt{2} \cdot \sigma_d}\right) \hspace{0.05cm}$$ gilt. Hierbei sind folgende Funktionen verwendet: $$\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm},$$ $${\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$ Die obige Gleichung gilt für den Schwellenwert E = 0 unabhängig von den Symbolwahrscheinlichkeiten pL und pH. Allerdings kann mit einem anderen Schwellenwert E eine kleinere Fehlerwahrscheinlichkeit erzielt werden, wenn die beiden Auftrittswahrscheinlichkeiten unterschiedlich sind (pL ≠ pH) Die Streuung des Rauschanteils ist stets σd = 0.5 V, die beiden Amplituden des Detektionsnutzanteils sind mit ±1 V fest vorgegeben. Zu untersuchen sind folgende Symbolwahrscheinlichkeiten:
- pL = 0.88 und pH = 0.12,
- pL = 0.31 und pH = 0.69.
In der Grafik ist dieser letzte Parametersatz und der Schwellenwert E = 0.1 · s0 dargestellt.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel1.2. Für die Ableitung der Q–Funktion gilt: $$\frac{{\rm d\hspace{0.05cm}Q} (\it x)} {{\rm d}\hspace{0.05cm}x} = \frac{\rm 1}{\sqrt{\rm 2\pi}} \cdot \rm e^{\it -x^{\rm 2}/\rm 2} \hspace{0.05cm}.$$ Die Werte der Funktion Q(x) können Sie mit folgendem Interaktionsmodul bestimmen:
Komplementäre Gaußsche Fehlerfunktionen
Fragebogen
Musterlösung