Aufgaben:Aufgabe 1.3: Kanalmodelle BSC–BEC–BSEC–AWGN: Unterschied zwischen den Versionen
| Zeile 34: | Zeile 34: | ||
*Bitte beachten Sie weiter: Ausgehend vom AWGN–Kanal ist die Verfälschungswahrscheinlichkeit $\varepsilon = 0$ eigentlich nicht möglich. | *Bitte beachten Sie weiter: Ausgehend vom AWGN–Kanal ist die Verfälschungswahrscheinlichkeit $\varepsilon = 0$ eigentlich nicht möglich. | ||
*Für diese Aufgabe behelfen wir uns dadurch, dass alle Wahrscheinlichkeiten in Prozent mit zwei Nachkommastellen angegeben werden sollen. Damit kann $\varepsilon < 0.5 · 10^{-4}$ durch $\varepsilon \approx 0$ angenähert werden. | *Für diese Aufgabe behelfen wir uns dadurch, dass alle Wahrscheinlichkeiten in Prozent mit zwei Nachkommastellen angegeben werden sollen. Damit kann $\varepsilon < 0.5 · 10^{-4}$ durch $\varepsilon \approx 0$ angenähert werden. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Zeile 80: | Zeile 81: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig ist die <u>Antwort 1</u> | + | '''(1)''' Richtig ist die <u>Antwort 1</u>: |
| + | *Das BSC–Modell basiert auf einer einzigen Entscheiderschwelle. Wegen der Eigenschaft ''Symmetric'' liegt diese bei $G = 0$. | ||
| − | |||
| + | '''(2)''' Die Wahrscheinlickeit, dass eine Gaußsche Zufallsgröße mit Streuung ''$\sigma$'' größer ist als $+1$ oder kleiner ist als $–1$, ergibt sich gemäß der Angabe zu $\varepsilon = {\rm Q} (1/ \sigma)$. Mit $\sigma= 0.4$ folgt daraus: | ||
| + | :$$\varepsilon = {\rm Q}(2.5) \ \underline { = 0.62\, \%}.$$ | ||
| − | |||
| + | '''(3)''' Richtig ist hier die <u>Antwort 2</u>: | ||
| + | *Beim BSEC–Modell gibt es drei Entscheidungsgebiete, je eines für die Symbole $0$ und $1$ und ein weiteres für ''Erasure'' ($\rm E$: keine Entscheidung möglich). | ||
| + | *Dazu benötigt man zwei Schwellen, die symmetrisch um $0$ liegen müssen. | ||
| + | *Wenn dem nicht so wäre, ergäben sich unterschiedliche Ergebnisse für die Symbole $0$ und $1$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(4)''' Es gelte $y_{\rm A} = \tilde{x}+ n$. Eine falsche Entscheidung ergibt sich in diesem Fall für den Rauschterm |
| − | + | *$n > +1.2$, falls $\tilde{x} = -1$ ⇒ $x = 1$, | |
| − | + | *$n < -1.2$, falls $\tilde{x} = +1$ ⇒ $x = 0$. | |
| − | '''(6)''' | + | In beiden Fällen erhält man für die Verfälschungswahrscheinlichkeit $ε = {\rm Q}(1.2/0.4) = {\rm Q}(3) \hspace{0.15cm} \underline{=0.14 \%}$. |
| + | Ein ''Erasure'' (keine Entscheidung) ergibt sich für $–0.2 < y_{\rm A} < +0.2$. Ausgehend von $\tilde{x} = -1$ gilt somit: | ||
| + | :$$\lambda \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.8 < n < 1.2) = {\rm Pr}(n > 0.8) - {\rm Pr}(n > 1.2) = {\rm Q}(2) - {\rm Q}(3) \approx 2.28\,\% - 0.14\,\% \hspace{0.15cm} \underline {\approx 2.14\,\%} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Hier ist ebenfalls die <u>Antwort 2</u> richtig: | ||
| + | *Auch beim BEC–Modell gibt es zwei um $0$ symmetrische Schwellen. Der Unterschied zum BSEC–Modell ist, dass sich die Verfälschungswahrscheinlichkeit $\varepsilon = 0$ (genauer gesagt: $\varepsilon < 0.5 · 10^{–4}$) ergibt, entweder, weil | ||
| + | *der Sicherheitsbereich $(±G)$ größer gewählt ist als beim BSEC–Modell, oder | ||
| + | *das AWGN–Rauschen eine kleinere Streuung $σ$ aufweist. | ||
| + | |||
| + | |||
| + | '''(6)''' Beim BEC–Modell ist die Verfälschungswahrscheinlichkeit vernachlässigbar: | ||
:$$\varepsilon = {\rm Q}(1.6/0.4) = {\rm Q}(4)\approx 0.32 \cdot 10^{-4} \approx 0 \hspace{0.05cm}.$$ | :$$\varepsilon = {\rm Q}(1.6/0.4) = {\rm Q}(4)\approx 0.32 \cdot 10^{-4} \approx 0 \hspace{0.05cm}.$$ | ||
Das heißt: Man kann hier tatsächlich vom BEC–Modell ausgehen. Für die ''Erasure''–Wahrscheinlichkeit gilt dabei: | Das heißt: Man kann hier tatsächlich vom BEC–Modell ausgehen. Für die ''Erasure''–Wahrscheinlichkeit gilt dabei: | ||
| − | :$${\it \lambda} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.4 < n < 1.6) = {\rm Pr}(n > 0.4) - {\rm Pr}(n > 1.6) = | + | :$${\it \lambda} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.4 < n < 1.6) = {\rm Pr}(n > 0.4) - {\rm Pr}(n > 1.6) ={\rm Q}(1) - {\rm Q}(4) \approx {\rm Q}(1) \hspace{0.15cm} \underline {= 15.87\,\%} \hspace{0.05cm}.$$ |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 11. Dezember 2017, 16:23 Uhr
Im Theorieteil zu diesem Kapitel werden die folgenden digitalen Kanalmodelle behandelt:
- Binary Symmetric Channel (BSC),
- Binary Erasure Channel (BEC),
- Binary Symmetric Error & Erasure Channel (BSEC).
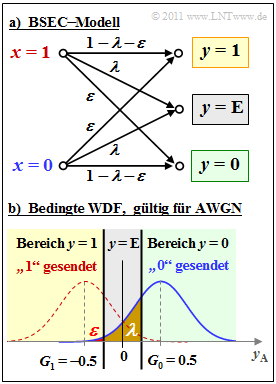
Die obere Grafik zeigt das BSEC–Modell. Daraus lassen sich zwei andere Kanalmodelle ableiten:
- Mit $λ = 0$ ergibt sich das BSC–Modell.
- Mit $\varepsilon = 0$ ergibt sich das BEC–Modell.
Die untere Grafik zeigt den Zusammenhang zwischen dem BSEC–Modell und dem analogen AWGN–Kanalmodell. Um Verwechslungen zu vermeiden, bezeichnen wir das (analoge) Ausgangssignal des AWGN–Kanals mit $y_{\rm A}$, wobei mit dem Rauschterm $n$ gilt: $y_{\rm A} = \tilde{x}+ n$.
Die Tilde weist auf die bipolare Beschreibung des Digitalsignals hin. Es gilt:
- $\tilde{x} = +1$, falls $x = 0$,
- $\tilde{x} = -1$, falls $x = 1$.
Man erkennt die ternäre Ausgangsgröße $y \in \{0, 1, \rm E\}$, die sich aus dem AWGN–Modell durch die Unterteilung in drei Bereiche ergibt. Hierzu werden die Entscheiderschwellen $G_0$ und $G_1$ benötigt.
$y = \rm E$ (Erasure) sagt aus, dass die Entscheidung so unsicher ist, dass als Ergebnis weder $y = 0$ noch $y = 1$ gerechtfertigt erscheint. In deutschen Fachbüchern spricht man von einer Auslöschung.
Hinweise:
- Die Aufgabe gehört zum Kapitel Kanalmodelle und Entscheiderstrukturen.
- Die Streuung des AWGN–Rauschens $n$ wird für die gesamte Aufgabe zu $\sigma = 0.4$ angenommen.
- Die Wahrscheinlichkeit, dass die Zufallsgröße $n$ größer ist als $A$ oder kleiner als $–A$, ergibt sich mit dem komplementären Gaußschen Fehlerintegral ${\rm Q}(x)$ wie folgt:
- $${\rm Pr}(n > A) = {\rm Pr}(n < -A) = {\rm Q}(A/\sigma)\hspace{0.05cm}.$$
- Bitte beachten Sie weiter: Ausgehend vom AWGN–Kanal ist die Verfälschungswahrscheinlichkeit $\varepsilon = 0$ eigentlich nicht möglich.
- Für diese Aufgabe behelfen wir uns dadurch, dass alle Wahrscheinlichkeiten in Prozent mit zwei Nachkommastellen angegeben werden sollen. Damit kann $\varepsilon < 0.5 · 10^{-4}$ durch $\varepsilon \approx 0$ angenähert werden.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Es folgen noch einige Zahlenwerte der Q–Funktion:
- $$ {\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 50.0\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(0.5) \ = \ 30.85\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1) \ = \ 15.87\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1.5) \ = \ 6.68\%\hspace{0.05cm},$$
- $${\rm Q}(2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2.28\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.5) \ = \ 0.62\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3) \ = \ 0.14\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3.5) \ = \ 0.02\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(4) \approx 0 \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- Das BSC–Modell basiert auf einer einzigen Entscheiderschwelle. Wegen der Eigenschaft Symmetric liegt diese bei $G = 0$.
(2) Die Wahrscheinlickeit, dass eine Gaußsche Zufallsgröße mit Streuung $\sigma$ größer ist als $+1$ oder kleiner ist als $–1$, ergibt sich gemäß der Angabe zu $\varepsilon = {\rm Q} (1/ \sigma)$. Mit $\sigma= 0.4$ folgt daraus:
- $$\varepsilon = {\rm Q}(2.5) \ \underline { = 0.62\, \%}.$$
(3) Richtig ist hier die Antwort 2:
- Beim BSEC–Modell gibt es drei Entscheidungsgebiete, je eines für die Symbole $0$ und $1$ und ein weiteres für Erasure ($\rm E$: keine Entscheidung möglich).
- Dazu benötigt man zwei Schwellen, die symmetrisch um $0$ liegen müssen.
- Wenn dem nicht so wäre, ergäben sich unterschiedliche Ergebnisse für die Symbole $0$ und $1$.
(4) Es gelte $y_{\rm A} = \tilde{x}+ n$. Eine falsche Entscheidung ergibt sich in diesem Fall für den Rauschterm
- $n > +1.2$, falls $\tilde{x} = -1$ ⇒ $x = 1$,
- $n < -1.2$, falls $\tilde{x} = +1$ ⇒ $x = 0$.
In beiden Fällen erhält man für die Verfälschungswahrscheinlichkeit $ε = {\rm Q}(1.2/0.4) = {\rm Q}(3) \hspace{0.15cm} \underline{=0.14 \%}$.
Ein Erasure (keine Entscheidung) ergibt sich für $–0.2 < y_{\rm A} < +0.2$. Ausgehend von $\tilde{x} = -1$ gilt somit:
- $$\lambda \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.8 < n < 1.2) = {\rm Pr}(n > 0.8) - {\rm Pr}(n > 1.2) = {\rm Q}(2) - {\rm Q}(3) \approx 2.28\,\% - 0.14\,\% \hspace{0.15cm} \underline {\approx 2.14\,\%} \hspace{0.05cm}.$$
(5) Hier ist ebenfalls die Antwort 2 richtig:
- Auch beim BEC–Modell gibt es zwei um $0$ symmetrische Schwellen. Der Unterschied zum BSEC–Modell ist, dass sich die Verfälschungswahrscheinlichkeit $\varepsilon = 0$ (genauer gesagt: $\varepsilon < 0.5 · 10^{–4}$) ergibt, entweder, weil
- der Sicherheitsbereich $(±G)$ größer gewählt ist als beim BSEC–Modell, oder
- das AWGN–Rauschen eine kleinere Streuung $σ$ aufweist.
(6) Beim BEC–Modell ist die Verfälschungswahrscheinlichkeit vernachlässigbar:
- $$\varepsilon = {\rm Q}(1.6/0.4) = {\rm Q}(4)\approx 0.32 \cdot 10^{-4} \approx 0 \hspace{0.05cm}.$$
Das heißt: Man kann hier tatsächlich vom BEC–Modell ausgehen. Für die Erasure–Wahrscheinlichkeit gilt dabei:
- $${\it \lambda} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(0.4 < n < 1.6) = {\rm Pr}(n > 0.4) - {\rm Pr}(n > 1.6) ={\rm Q}(1) - {\rm Q}(4) \approx {\rm Q}(1) \hspace{0.15cm} \underline {= 15.87\,\%} \hspace{0.05cm}.$$