Aufgaben:Aufgabe 1.2Z: Nochmals Lognormal–Fading: Unterschied zwischen den Versionen
| Zeile 69: | Zeile 69: | ||
| − | {Welche Aussagen gelten für die mittlere Empfangsleistung ${\rm E}\big[P_{\rm E}(t)\big]$? <br><u>Hinweis:</u> $P_{\rm E}\hspace{0.01cm}'$ ist die Leistung nach der Multiplikation mit $k_1$ (siehe Grafik). | + | {Welche Aussagen gelten für die mittlere Empfangsleistung ${\rm E}\big[P_{\rm E}(t)\big]$? <br><u>Hinweis:</u> $P_{\rm E}\hspace{0.01cm}'$ ist die Leistung nach der Multiplikation mit $k_1$ (siehe Grafik). |
|type="()"} | |type="()"} | ||
- Es gilt: ${\rm E}[P_{\rm E}(t)] = P_{\rm E}\hspace{0.01cm}'$. | - Es gilt: ${\rm E}[P_{\rm E}(t)] = P_{\rm E}\hspace{0.01cm}'$. | ||
| Zeile 78: | Zeile 78: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Konstante $k_1$ erzeugt den zeitunabhängigen Pfadverlust $V_1 = 60 \ \rm dB$. Daraus folgt: | + | '''(1)''' Die Konstante $k_1$ erzeugt den zeitunabhängigen Pfadverlust $V_1 = 60 \ \rm dB$. Daraus folgt: |
:$$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$ | :$$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$ | ||
| + | |||
'''(2)''' Richtig ist nur der <u>zweite Lösungsvorschlag</u>: | '''(2)''' Richtig ist nur der <u>zweite Lösungsvorschlag</u>: | ||
| − | *Für die Gaußsche Zufallsvariable $V_2$ sind (theoretisch) alle Werte zwischen | + | *Für die Gaußsche Zufallsvariable $V_2$ sind (theoretisch) alle Werte zwischen $-∞$ und $+∞$ möglich. |
| − | *Durch die Transformation $z_2 = 10^{{\it | + | *Durch die Transformation $z_2 = 10^{{\it -V_2}\rm /20}$ ergeben sich für die lineare Zufallsgröße $z_2$ nur positive Werte und zwar zwischen 0 $($falls $V_2$ positiv ist und bis ins Unendliche reicht$)$ und $+∞$ $($für sehr große negative Werte von $V_2)$. |
| − | '''(3)''' Die Zufallsgröße $z_2$ kann nur positiv sein. Deshalb ist der WDF–Wert $f_{\rm z2}(z_2 = 0)\hspace{0.15cm} \underline{ = 0}$. | + | '''(3)''' Die Zufallsgröße $z_2$ kann nur positiv sein. Deshalb ist der WDF–Wert $f_{\rm z2}(z_2 = 0)\hspace{0.15cm} \underline{ = 0}$. |
| − | *Der WDF–Wert für den Abszissenwert $z_2 = 1$ erhält man durch Einsetzen in die gegebene Gleichung: | + | *Der WDF–Wert für den Abszissenwert $z_2 = 1$ erhält man durch Einsetzen in die gegebene Gleichung: |
| − | :$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | + | :$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}=1) |
| + | /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) | ||
| + | } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)} = | ||
\frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } | \frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } | ||
\hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$ | \hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$ | ||
| − | *Der erste Anteil ist gleich dem WDF–Wert $f_{{\it V}2}(V_2 = 0)$. | + | *Der erste Anteil ist gleich dem WDF–Wert $f_{{\it V}2}(V_2 = 0)$. |
| − | *$C$ berücksichtigt den Betrag der Ableitung der nichtlinearen Kennlinie $z_2 = g(V_2)$ für $V_2 = 0 \ \rm dB$ bzw. $z_2 = 1$. | + | *$C$ berücksichtigt den Betrag der Ableitung der nichtlinearen Kennlinie $z_2 = g(V_2)$ für $V_2 = 0 \ \rm dB$ bzw. $z_2 = 1$. |
| − | *Schließlich erhält man für $z_2 = 2$: | + | *Schließlich erhält man für $z_2 = 2$: |
:$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot | :$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot | ||
| − | {\rm | + | {\rm e }^{ - {{\rm ln}^2 (2)}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}C^2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2)} = {0.578}/{ 2} \cdot |
| − | {\rm | + | {\rm e } ^{ - {0.48}/{0.952} } \hspace{0.15cm} \underline{\approx 0.174}\hspace{0.05cm}. $$ |
| − | '''(4)''' Berücksichtigt man den Zusammenhang zwischen $z_2$ und $V_2$, so erhält man: | + | '''(4)''' Berücksichtigt man den Zusammenhang zwischen $z_2$ und $V_2$, so erhält man: |
:$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} | :$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Zeile 111: | Zeile 114: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Die Wahrscheinlichkeit, dass eine Gaußvariable größer ist als $2 \cdot \sigma$, ist aber gleich ${\rm Q}(2)$: | + | *Die Wahrscheinlichkeit, dass eine Gaußvariable größer ist als $2 \cdot \sigma$, ist aber gleich ${\rm Q}(2)$: |
:$${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023} | :$${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 117: | Zeile 120: | ||
'''(5)''' Richtig ist der <u>Lösungsvorschlag 3</u>: | '''(5)''' Richtig ist der <u>Lösungsvorschlag 3</u>: | ||
| − | *Die erste Aussage ist mit Sicherheit nicht zutreffend, da sich der Mittelwert $m_{\rm S}$ auf die logarithmierte Empfangsleistung (in $\rm dBm$ | + | *Die erste Aussage ist mit Sicherheit nicht zutreffend, da sich der Mittelwert $m_{\rm S}$ auf die logarithmierte Empfangsleistung $($in $\rm dBm)$ bezieht. |
| − | *Um zu klären, ob nun die zweite oder die dritte Lösungsalternative zutrifft, gehen wir von $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ und folgender $V_2$–WDF aus: | + | *Um zu klären, ob nun die zweite oder die dritte Lösungsalternative zutrifft, gehen wir von $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ und folgender $V_2$–WDF aus: |
:$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) | :$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) | ||
+ 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$ | + 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$ | ||
| − | *In der Hälfte der Zeit ist dann $P_{\rm E} = 1 \ \rm µ W$, während in den beiden anderen Vierteln jeweils gilt: | + | *In der Hälfte der Zeit ist dann $P_{\rm E} = 1 \ \rm µ W$, während in den beiden anderen Vierteln jeweils gilt: |
:$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\rm µ W}\hspace{0.05cm},$$ | :$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\rm µ W}\hspace{0.05cm},$$ | ||
:$$V_{\rm 2}= -10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\rm µ W}\hspace{0.05cm}.$$ | :$$V_{\rm 2}= -10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\rm µ W}\hspace{0.05cm}.$$ | ||
| − | *Der Mittelwert ergibt somit: | + | *Der Mittelwert ergibt somit zu: |
| − | :$${\rm E}[P_{\rm E}(t)] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W} | + | :$${\rm E}\big[P_{\rm E}(t)\big] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Diese einfache Rechnung mit diskreten Wahrscheinlichkeiten anstelle einer kontinuierlichen WDF deutet darauf hin, dass der <u>Lösungsvorschlag 3</u> richtig | + | *Diese einfache Rechnung mit diskreten Wahrscheinlichkeiten anstelle einer kontinuierlichen WDF deutet darauf hin, dass der <u>Lösungsvorschlag 3</u> richtig ist. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 10. Mai 2020, 14:22 Uhr
Wir gehen von ähnlichen Bedingungen wie in der Aufgabe 1.2 aus, fassen aber nun den rein entfernungsabhängigen Pfadverlust $V_0$ und den Mittelwert $m_{\rm S}$ des Lognormal–Fadings zusammen (der Index „S” steht für Shadowing):
- $$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$
Der gesamte Pfadverlust ist dann durch die Gleichung
- $$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$
gegeben, wobei $V_2(t)$ eine Lognormal–Verteilung mit Mittelwert Null beschreibt:
- $$f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) }\hspace{0.05cm}.$$
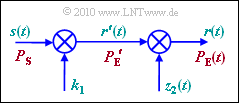
Das in der Grafik gezeigte Pfadverlustmodell ist für das hier beschriebene Szenario geeignet:
- Multipliziert man das Sendesignal $s(t)$ zunächst mit einem konstanten Faktor $k_1$ und weiter mit einer stochastischen Größe $z_2(t)$ mit der Wahrscheinlichkeitsdichte $\rm (WDF)$ $f_{\rm z2}(z_2)$, so ergibt sich am Ausgang das Signal $r(t)$, dessen Leistung $P_{\rm E}(t)$ aufgrund des stochastischen Anteils natürlich ebenfalls zeitabhängig ist.
- Die WDF der lognormalverteilten Zufallsgröße $z_2$ lautet für $z_2 ≥ 0$:
- $$f_{z_{\rm 2}}(z_{\rm 2}) = \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}) /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.8cm}{\rm mit} \hspace{0.8cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$
- Für $z_2 ≤ 0$ ist diese WDF identisch Null.
Hinweise:
- Die Aufgabe gehört zum Kapitel Distanzabhängige Dämpfung und Abschattung.
- Verwenden Sie folgende Kenngrößen:
- $$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$
- Die Wahrscheinlichkeit, dass eine mittelwertfreie Gaußsche Zufallsgröße $z$ größer ist als ihre Streuung $\sigma$, lautet:
- $${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$
- Außerdem gilt: ${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$
- Nochmals zur Verdeutlichung: $z_2$ ist die lineare Fading–Größe, während die Beschreibungsgröße $V_2$ auf dem Zehner–Logarithmus basiert.
- Es gelten folgende Umrechnungen:
- $$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$
(2) Richtig ist nur der zweite Lösungsvorschlag:
- Für die Gaußsche Zufallsvariable $V_2$ sind (theoretisch) alle Werte zwischen $-∞$ und $+∞$ möglich.
- Durch die Transformation $z_2 = 10^{{\it -V_2}\rm /20}$ ergeben sich für die lineare Zufallsgröße $z_2$ nur positive Werte und zwar zwischen 0 $($falls $V_2$ positiv ist und bis ins Unendliche reicht$)$ und $+∞$ $($für sehr große negative Werte von $V_2)$.
(3) Die Zufallsgröße $z_2$ kann nur positiv sein. Deshalb ist der WDF–Wert $f_{\rm z2}(z_2 = 0)\hspace{0.15cm} \underline{ = 0}$.
- Der WDF–Wert für den Abszissenwert $z_2 = 1$ erhält man durch Einsetzen in die gegebene Gleichung:
- $$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {{\rm e^{- {\rm ln}^2 (z_{\rm 2}=1) /({2 \hspace{0.05cm}\cdot \hspace{0.05cm} C^2 \hspace{0.05cm} \cdot \hspace{0.05cm} \sigma_{\rm S}^2}) } } }{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)} = \frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } \hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$
- Der erste Anteil ist gleich dem WDF–Wert $f_{{\it V}2}(V_2 = 0)$.
- $C$ berücksichtigt den Betrag der Ableitung der nichtlinearen Kennlinie $z_2 = g(V_2)$ für $V_2 = 0 \ \rm dB$ bzw. $z_2 = 1$.
- Schließlich erhält man für $z_2 = 2$:
- $$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot {\rm e }^{ - {{\rm ln}^2 (2)}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}C^2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2)} = {0.578}/{ 2} \cdot {\rm e } ^{ - {0.48}/{0.952} } \hspace{0.15cm} \underline{\approx 0.174}\hspace{0.05cm}. $$
(4) Berücksichtigt man den Zusammenhang zwischen $z_2$ und $V_2$, so erhält man:
- $${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} \hspace{0.05cm},$$
- $${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842} \hspace{0.05cm},$$
- $${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > 2 \sigma_{\rm S}) \hspace{0.05cm}.$$
- Die Wahrscheinlichkeit, dass eine Gaußvariable größer ist als $2 \cdot \sigma$, ist aber gleich ${\rm Q}(2)$:
- $${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023} \hspace{0.05cm}.$$
(5) Richtig ist der Lösungsvorschlag 3:
- Die erste Aussage ist mit Sicherheit nicht zutreffend, da sich der Mittelwert $m_{\rm S}$ auf die logarithmierte Empfangsleistung $($in $\rm dBm)$ bezieht.
- Um zu klären, ob nun die zweite oder die dritte Lösungsalternative zutrifft, gehen wir von $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$ ⇒ $P_{\rm E}' = 1 \ {\rm µ W}$ und folgender $V_2$–WDF aus:
- $$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) + 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$
- In der Hälfte der Zeit ist dann $P_{\rm E} = 1 \ \rm µ W$, während in den beiden anderen Vierteln jeweils gilt:
- $$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\rm µ W}\hspace{0.05cm},$$
- $$V_{\rm 2}= -10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\rm µ W}\hspace{0.05cm}.$$
- Der Mittelwert ergibt somit zu:
- $${\rm E}\big[P_{\rm E}(t)\big] = 0.5 \cdot 1\,{\rm µ W}+ 0.25 \cdot 0.1\,{\rm µ W}+0.25 \cdot 10\,{\rm µ W}= 3.025\,{\rm µ W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm µ W} \hspace{0.05cm}.$$
- Diese einfache Rechnung mit diskreten Wahrscheinlichkeiten anstelle einer kontinuierlichen WDF deutet darauf hin, dass der Lösungsvorschlag 3 richtig ist.