Aufgaben:Aufgabe 1.2Z: Messung der Übertragungsfunktion: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
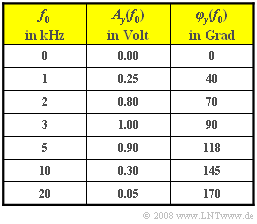
[[Datei:P_ID788__LZI_Z_1_2.png |right|Gemessene Signalamplituden <br>und Phasen bei Filter $\rm B$|frame]] | [[Datei:P_ID788__LZI_Z_1_2.png |right|Gemessene Signalamplituden <br>und Phasen bei Filter $\rm B$|frame]] | ||
| − | Zur messtechnischen Bestimmung des Filterfrequenzgangs wird ein sinusförmiges Eingangssignal mit der Amplitude $2 \hspace{0.05cm} \text{V}$ und vorgegebener Frequenz $f_0$ angelegt. Das Ausgangssignal $y(t)$ bzw. dessen Spektrum $Y(f)$ werden dann nach Betrag und Phase ermittelt. | + | Zur messtechnischen Bestimmung des Filterfrequenzgangs wird ein sinusförmiges Eingangssignal mit der Amplitude $2 \hspace{0.05cm} \text{V}$ und vorgegebener Frequenz $f_0$ angelegt. Das Ausgangssignal $y(t)$ bzw. dessen Spektrum $Y(f)$ werden dann nach Betrag und Phase ermittelt. |
*Das Betragsspektrum am Ausgang von Filter $\rm A$ lautet mit der Frequenz $f_0 = 1 \ \text{kHz}$: | *Das Betragsspektrum am Ausgang von Filter $\rm A$ lautet mit der Frequenz $f_0 = 1 \ \text{kHz}$: | ||
:$$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f | :$$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f | ||
\pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ | \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ | ||
| − | *Bei einem anderen Filter $\rm B$ ist das Ausgangssignal dagegen stets eine harmonische Schwingung mit der (einzigen) Frequenz $f_0$. Bei den in der Tabelle angegebenen Frequenzen $f_0$ werden die Amplituden $A_y(f_0)$ und die Phasen $φ_y(f_0)$ gemessen. Hierbei gilt: | + | *Bei einem anderen Filter $\rm B$ ist das Ausgangssignal dagegen stets eine harmonische Schwingung mit der (einzigen) Frequenz $f_0$. Bei den in der Tabelle angegebenen Frequenzen $f_0$ werden die Amplituden $A_y(f_0)$ und die Phasen $φ_y(f_0)$ gemessen. Hierbei gilt: |
:$$Y_{\rm B} (f) = {A_y}/{2} \cdot {\rm e}^{ {\rm j} \varphi_y} | :$$Y_{\rm B} (f) = {A_y}/{2} \cdot {\rm e}^{ {\rm j} \varphi_y} | ||
\cdot {\rm \delta } (f + f_0) + {A_y}/{2} \cdot {\rm e}^{ | \cdot {\rm \delta } (f + f_0) + {A_y}/{2} \cdot {\rm e}^{ | ||
| Zeile 19: | Zeile 19: | ||
dargestellt werden. Hierbei bezeichnet | dargestellt werden. Hierbei bezeichnet | ||
| − | *$a_{\rm B}( | + | *$a_{\rm B}(f_0)$ den Dämpfungsverlauf, und |
| − | *$b_{\rm B}( | + | *$b_{\rm B}(f_0)$ den Phasenverlauf. |
| Zeile 71: | Zeile 71: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | '''(1)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| − | *Bei einem LZI–System gilt $Y(f) = X(f) · H(f)$. | + | *Bei einem LZI–System gilt $Y(f) = X(f) · H(f)$. |
| − | *Daher ist es nicht möglich, dass im Ausgangssignal ein Anteil mit $3 f_0$ vorhanden ist, wenn ein solcher im Eingangssignal fehlt. | + | *Daher ist es nicht möglich, dass im Ausgangssignal ein Anteil mit $3 f_0$ vorhanden ist, wenn ein solcher im Eingangssignal fehlt. |
| − | *Das heißt: Es liegt hier kein LZI–System vor und dementsprechend ist auch kein Frequenzgang angebbar. | + | *Das heißt: Es liegt hier kein LZI–System vor und dementsprechend ist auch kein Frequenzgang angebbar. |
| + | |||
'''(2)''' Richtig ist der <u>Lösungsvorschlag 3</u>: | '''(2)''' Richtig ist der <u>Lösungsvorschlag 3</u>: | ||
| − | *Aufgrund der angegeben Zahlenwerte für $A_y(f_0)$ kann von einem <u>Bandpass</u> ausgegangen werden. | + | *Aufgrund der angegeben Zahlenwerte für $A_y(f_0)$ kann von einem <u>Bandpass</u> ausgegangen werden. |
| − | '''(3)''' Mit $A_x = 2 \text{ V}$ und $\varphi_x = 90^\circ$ (Sinusfunktion) erhält man für $f_0 = f_3 =3 \text{ kHz}$: | + | |
| + | '''(3)''' Mit $A_x = 2 \text{ V}$ und $\varphi_x = 90^\circ$ (Sinusfunktion) erhält man für $f_0 = f_3 =3 \text{ kHz}$: | ||
:$$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} | :$$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} | ||
(\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm | (\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm | ||
V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | ||
90^{\circ})} = 0.5.$$ | 90^{\circ})} = 0.5.$$ | ||
| − | Somit ergeben sich für $f_0 = f_3 = 3 \text{ kHz}$ die Werte | + | Somit ergeben sich für $f_0 = f_3 = 3 \text{ kHz}$ die Werte |
*$a_{\rm B} (f_3)\rm \underline{\: ≈ \: 0.693 \: Np}$, | *$a_{\rm B} (f_3)\rm \underline{\: ≈ \: 0.693 \: Np}$, | ||
*$b_{\rm B}(f_3) \rm \underline{\: = \: 0 \: (Grad)}$. | *$b_{\rm B}(f_3) \rm \underline{\: = \: 0 \: (Grad)}$. | ||
| − | '''(4)''' In analoger Weise kann der Frequenzgang bei $f_0 = f_2 =2 \text{ kHz}$ ermittelt werden: | + | '''(4)''' In analoger Weise kann der Frequenzgang bei $f_0 = f_2 =2 \text{ kHz}$ ermittelt werden: |
:$$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm | :$$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm | ||
V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - | ||
70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$ | 70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$ | ||
| − | Damit erhält man für $f_0 = f_2 = 2 \ \text{ kHz}$: | + | Damit erhält man für $f_0 = f_2 = 2 \ \text{ kHz}$: |
*$a_{\rm B}(f_2) \rm \underline{\: ≈ \: 0.916 \: Np}$, | *$a_{\rm B}(f_2) \rm \underline{\: ≈ \: 0.916 \: Np}$, | ||
* $b_{\rm B}(f_2) \rm \underline{\: = \: 20°}$. | * $b_{\rm B}(f_2) \rm \underline{\: = \: 20°}$. | ||
| − | Bei $f_0 = -f_2 =-\hspace{-0.01cm}2 \text{ kHz}$ gilt der gleiche Dämpfungswert. | + | Bei $f_0 = -f_2 =-\hspace{-0.01cm}2 \text{ kHz}$ gilt der gleiche Dämpfungswert. Die Phase hat jedoch das umgekehrte Vorzeichen. Also ist $b_{\rm B}(–f_2) = \ –\hspace{-0.01cm}20^{\circ}.$ |
| − | |||
| − | Die Phase hat jedoch das umgekehrte Vorzeichen. Also ist $b_{\rm B}(–f_2) = \ –\hspace{-0.01cm}20^{\circ}.$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 11. Juli 2021, 17:58 Uhr
Zur messtechnischen Bestimmung des Filterfrequenzgangs wird ein sinusförmiges Eingangssignal mit der Amplitude $2 \hspace{0.05cm} \text{V}$ und vorgegebener Frequenz $f_0$ angelegt. Das Ausgangssignal $y(t)$ bzw. dessen Spektrum $Y(f)$ werden dann nach Betrag und Phase ermittelt.
- Das Betragsspektrum am Ausgang von Filter $\rm A$ lautet mit der Frequenz $f_0 = 1 \ \text{kHz}$:
- $$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$
- Bei einem anderen Filter $\rm B$ ist das Ausgangssignal dagegen stets eine harmonische Schwingung mit der (einzigen) Frequenz $f_0$. Bei den in der Tabelle angegebenen Frequenzen $f_0$ werden die Amplituden $A_y(f_0)$ und die Phasen $φ_y(f_0)$ gemessen. Hierbei gilt:
- $$Y_{\rm B} (f) = {A_y}/{2} \cdot {\rm e}^{ {\rm j} \varphi_y} \cdot {\rm \delta } (f + f_0) + {A_y}/{2} \cdot {\rm e}^{ -{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$
Das Filter $\rm B$ soll in der Aufgabe in der Form
- $$H_{\rm B}(f) = {\rm e}^{-a_{\rm B}(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_{\rm B}(f)}$$
dargestellt werden. Hierbei bezeichnet
- $a_{\rm B}(f_0)$ den Dämpfungsverlauf, und
- $b_{\rm B}(f_0)$ den Phasenverlauf.
Hinweis:
- Die Aufgabe gehört zum Kapitel Systembeschreibung im Frequenzbereich.
Fragebogen
Musterlösung
- Bei einem LZI–System gilt $Y(f) = X(f) · H(f)$.
- Daher ist es nicht möglich, dass im Ausgangssignal ein Anteil mit $3 f_0$ vorhanden ist, wenn ein solcher im Eingangssignal fehlt.
- Das heißt: Es liegt hier kein LZI–System vor und dementsprechend ist auch kein Frequenzgang angebbar.
(2) Richtig ist der Lösungsvorschlag 3:
- Aufgrund der angegeben Zahlenwerte für $A_y(f_0)$ kann von einem Bandpass ausgegangen werden.
(3) Mit $A_x = 2 \text{ V}$ und $\varphi_x = 90^\circ$ (Sinusfunktion) erhält man für $f_0 = f_3 =3 \text{ kHz}$:
- $$H_{\rm B} (f_3) = \frac{A_y}{A_x} \cdot {\rm e}^{ -{\rm j} (\varphi_x - \varphi_y)} = \frac{1\hspace{0.05cm}{\rm V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - 90^{\circ})} = 0.5.$$
Somit ergeben sich für $f_0 = f_3 = 3 \text{ kHz}$ die Werte
- $a_{\rm B} (f_3)\rm \underline{\: ≈ \: 0.693 \: Np}$,
- $b_{\rm B}(f_3) \rm \underline{\: = \: 0 \: (Grad)}$.
(4) In analoger Weise kann der Frequenzgang bei $f_0 = f_2 =2 \text{ kHz}$ ermittelt werden:
- $$H_{\rm B} ( f_2) = \frac{0.8\hspace{0.05cm}{\rm V}}{2\hspace{0.05cm}{\rm V}} \cdot {\rm e}^{ -{\rm j} (90^{\circ} - 70^{\circ})} = 0.4\cdot {\rm e}^{ -{\rm j} 20^{\circ}}.$$
Damit erhält man für $f_0 = f_2 = 2 \ \text{ kHz}$:
- $a_{\rm B}(f_2) \rm \underline{\: ≈ \: 0.916 \: Np}$,
- $b_{\rm B}(f_2) \rm \underline{\: = \: 20°}$.
Bei $f_0 = -f_2 =-\hspace{-0.01cm}2 \text{ kHz}$ gilt der gleiche Dämpfungswert. Die Phase hat jedoch das umgekehrte Vorzeichen. Also ist $b_{\rm B}(–f_2) = \ –\hspace{-0.01cm}20^{\circ}.$