Aufgaben:Aufgabe 1.2Z: Linear verzerrendes System: Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
*Die Leistungen $P_q$ und $P_ε$ sind die quadratischen Mittelwerte der Signale $q(t)$ und $ε(t)$ und können bei periodischen Signalen mit der Periodendauer $T_0$ wie folgt ermittelt werden: | *Die Leistungen $P_q$ und $P_ε$ sind die quadratischen Mittelwerte der Signale $q(t)$ und $ε(t)$ und können bei periodischen Signalen mit der Periodendauer $T_0$ wie folgt ermittelt werden: | ||
:$$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | :$$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | ||
| + | *Die Angabe von Leistungen in $\rm V^2$ bedeutet, dass die Signale auf den Widerstand $R = 1\ \rm \Omega$ bezogen werden. | ||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| Zeile 40: | Zeile 41: | ||
| − | {Wie groß ist der Maximalwert des Fehlersignals $ε_1(t) = v_1(t) | + | {Wie groß ist der Maximalwert des Fehlersignals $ε_1(t) = v_1(t) - q(t)$? |
|type="{}"} | |type="{}"} | ||
$ε_\text{1, max} \ = \ $ { 1 3% } $\ \rm V$ | $ε_\text{1, max} \ = \ $ { 1 3% } $\ \rm V$ | ||
| Zeile 50: | Zeile 51: | ||
{Berechnen Sie die Nutzleistung $P_q$ und das Sinken–SNR $ρ_{v1}$. | {Berechnen Sie die Nutzleistung $P_q$ und das Sinken–SNR $ρ_{v1}$. | ||
|type="{}"} | |type="{}"} | ||
| − | $P_q\ = \ $ { 2 3% } $V^ | + | $P_q\ = \ $ { 2 3% } $\ \rm V^2$ |
$ρ_{v1} \ = \ $ { 6 3% } | $ρ_{v1} \ = \ $ { 6 3% } | ||
| Zeile 57: | Zeile 58: | ||
$Δt_2/T_0 \ = \ $ { 0.25 3% } | $Δt_2/T_0 \ = \ $ { 0.25 3% } | ||
| − | {Ermitteln Sie das Fehlersignal $ε_2(t) = v_2(t) | + | {Ermitteln Sie das Fehlersignal $ε_2(t) = v_2(t) - q(t)$, die Verzerrungsleistung $P_{ε2}$ und das Sinken–$\text{SNR} $ρ_{v2}$. |
|type="{}"} | |type="{}"} | ||
$P_{ε2} \ = \ $ { 0.167 3% } $\ \rm V^2$ | $P_{ε2} \ = \ $ { 0.167 3% } $\ \rm V^2$ | ||
| Zeile 69: | Zeile 70: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Allgemein gilt $v(t) = q(t) ∗ h(t)$. Die Faltung des periodischen Rechtecksignals $q(t)$ mit der ebenfalls rechteckförmigen Impulsantwort $h(t)$ liefert nur dann ein Dreiecksignal $v(t)$, wenn die miteinander gefalteten Rechtecke gleiche Breite haben. Daraus folgt: |
| − | $$\Delta t_1 = T_0 /2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \Delta t_1 / T_0\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | + | :$$\Delta t_1 = T_0 /2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \Delta t_1 / T_0\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ |
| − | [[Datei:P_ID958__Mod_Z_1_2_b.png|right|]] | + | [[Datei:P_ID958__Mod_Z_1_2_b.png|right|frame|Fehlersignale bei den beiden betrachteten Empfangsfiltern unterschiedlicher Breite]] |
| − | '''2 | + | '''(2)''' Das Fehlersignal $ε_1(t)$ ist in nebenstehender Grafik oben dargestellt. Man erkennt, dass $ε_1(t)$ alle Werte zwischen $±1 \ \rm V$ annehmen kann: |
| − | $${\varepsilon}_{ | + | :$${\varepsilon}_\text{ 1, max} \hspace{0.15cm}\underline {= {1}\;{\rm V}} \hspace{0.05cm}.$$ |
| − | '''3 | + | '''(3)''' Es genügt die Mittelung über den Zeitbereich von$t = 0$ bis $t =T_0/4$, da alle anderen Teilintervalle genau gleiche Beiträge liefern: |
| − | $$P_{\varepsilon{\rm 1}} = \frac{1}{T_{\rm 0}/4} \cdot \ | + | :$$P_{\varepsilon{\rm 1}} = \frac{1}{T_{\rm 0}/4} \cdot \int_{0}^{ T_{\rm 0}/4} {\varepsilon_1(t)^2 }\hspace{0.1cm}{\rm d}t = \frac{1 \,{\rm V}^2}{T_{\rm 0}/4} \cdot \int_{0}^{ T_{\rm 0}/4} {\left( 1 - \frac{t}{T_{\rm 0}/4}\right)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ |
Mit der Substitution $x = 4 · t/T_0$ kann hierfür auch geschrieben werden: | Mit der Substitution $x = 4 · t/T_0$ kann hierfür auch geschrieben werden: | ||
| − | $$P_{\varepsilon{\rm 1}} = 1 \,{\rm V}^2 \cdot \ | + | :$$P_{\varepsilon{\rm 1}} = 1 \,{\rm V}^2 \cdot \int_{0}^{ 1} {\left( 1 - 2x + x^2\right)}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}= 1 \,{\rm V}^2 \cdot \left( 1 - 1 + \frac{1}{3}\right)\hspace{0.15cm}\underline {= 0.333} \,{\rm V}^2\hspace{0.05cm}.$$ |
| − | '''4 | + | '''(4)''' Die Mittelung über eine Periode des quadrierten Quellensignals liefert: |
| − | $$P_{q} = \frac{1}{T_0} \cdot \left[(2\,{\rm V})^2 \cdot \frac{T_0}{2}+(0\,{\rm V})^2 \cdot \frac{T_0}{2} \right]\hspace{0.15cm}\underline {= 2\,{\rm V^2}}\hspace{0.05cm}.$$ | + | :$$P_{q} = \frac{1}{T_0} \cdot \left[(2\,{\rm V})^2 \cdot \frac{T_0}{2}+(0\,{\rm V})^2 \cdot \frac{T_0}{2} \right]\hspace{0.15cm}\underline {= 2\,{\rm V^2}}\hspace{0.05cm}.$$ |
Das Sinken–SNR beträgt somit | Das Sinken–SNR beträgt somit | ||
| − | $$\rho_{v{\rm 1}} = \frac{P_{q}}{P_{\varepsilon {\rm 1}}} = \frac{2 \,{\rm V}^2}{0.333 \,{\rm V}^2}\hspace{0.15cm}\underline {= 6} \hspace{0.05cm}.$$ | + | :$$\rho_{v{\rm 1}} = \frac{P_{q}}{P_{\varepsilon {\rm 1}}} = \frac{2 \,{\rm V}^2}{0.333 \,{\rm V}^2}\hspace{0.15cm}\underline {= 6} \hspace{0.05cm}.$$ |
| − | |||
| + | '''(5)''' Entsprechend der Skizze auf dem Angabenblatt wird nun aus einem Rechteck der Dauer $0.5 \cdot T_0$ ein Trapez der absoluten Dauer $0.75 · T_0$. Damit ist nach den Gesetzen der Faltung offensichtlich, dass die äquivalente Impulsdauer $Δt_2/T_0\hspace{0.15cm}\underline { = 0.25}$ sein muss. | ||
| − | |||
| − | |||
| − | |||
| − | '''7 | + | '''(6)''' Die untere Skizze in obiger Grafik zeigt, dass sich $ε_2(t)$ ebenso wie $ε_1(t)$ innerhalb einer Periodendauer $T_0$ aus vier Dreiecken zusammensetzt, doch sind diese nur halb so breit. In der Hälfte der Zeit ist nämlich $ε_2(t) = 0$. |
| + | |||
| + | Wegen $ε_\text{2, max} = ε_\text{1, max} = 1 \ \rm V$ erhält man: | ||
| + | :$$P_{\varepsilon{\rm 2}} ={P_{\varepsilon{\rm 1}}}/{2} \hspace{0.15cm}\underline {= 0.167} \,{\rm V}^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 2}} = {P_{q}}/{P_{\varepsilon {\rm 2}}}\hspace{0.15cm}\underline {= 12} \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(7)''' Für $Δt = T_0/2$ wurde in der Teilaufgabe (3) die Verzerrungsleistung $P_{ε1} = 1/3 \ \rm V^{ 2 }$ berechnet. In der Teilaufgabe(6) wurde gezeigt, dass bei $Δt = T_0/4$ die Verzerrungsleistung $P_{ε2}$ nur halb so groß ist. | ||
Anschaulich wurde erläutert, dass ein linearer Zusammenhang besteht. Daraus folgen für $Δt ≤ T_0/2$ die empirischen Gleichungen: | Anschaulich wurde erläutert, dass ein linearer Zusammenhang besteht. Daraus folgen für $Δt ≤ T_0/2$ die empirischen Gleichungen: | ||
| − | $$P_{\varepsilon} = \frac{2 \,{\rm V}^2}{3} \cdot \frac{\Delta t}{T_0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} = \frac{P_{q}}{P_{\varepsilon }}= \frac{3}{\Delta t/T_0} \hspace{0.05cm}.$$ | + | :$$P_{\varepsilon} = \frac{2 \,{\rm V}^2}{3} \cdot \frac{\Delta t}{T_0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} = \frac{P_{q}}{P_{\varepsilon }}= \frac{3}{\Delta t/T_0} \hspace{0.05cm}.$$ |
| − | Der Sonderfall $Δt = | + | Der Sonderfall $Δt = T_0/20$ führt somit zu den Resultaten: |
| − | $$P_{\varepsilon{\rm 3}} = \frac{2 \,{\rm V}^2}{60} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 3}} = \frac{P_{q}}{P_{\varepsilon {\rm 3}}}\hspace{0.15cm}\underline {= 60} \hspace{0.05cm}.$$ | + | :$$P_{\varepsilon{\rm 3}} = \frac{2 \,{\rm V}^2}{60} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 3}} = \frac{P_{q}}{P_{\varepsilon {\rm 3}}}\hspace{0.15cm}\underline {= 60} \hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 19. Juni 2017, 17:37 Uhr
Modulator, Kanal und Demodulator einer Einrichtung zur Nachrichtenübertragung können durch ein einziges lineares System mit dem Frequenzgang
- $$ H(f) = {\rm si }( \pi \cdot f \cdot \Delta t)$$
beschrieben werden. Die dazugehörige Impulsantwort ist rechteckförmig, symmetrisch um $t = 0$ und weist die Höhe $1/Δt$ sowie die (äquivalente) Dauer $Δt$ auf:
- $$ h(t) = \left\{ \begin{array}{c} 1/\Delta t \\ 1/(2\Delta t) \\ 0 \\ \end{array} \right. \begin{array}{*{4}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| < \Delta t/2,} \\ {\left| \hspace{0.005cm}t\hspace{0.05cm} \right| = \Delta t/2,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > \Delta t/2.} \\ \end{array}$$
Es handelt sich um einen Spalttiefpass, der im Kapitel Einige systemtheoretische Tiefpassfunktionen des Buches „Lineare zeitinvariante Systeme” eingehend behandelt wurde.
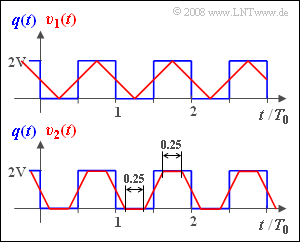
Am Systemeingang liegt das periodische Rechtecksignal $q(t)$ mit der Periodendauer $T_0$ an. Die Dauer der einzelnen Rechtecke und die der Lücken sind somit jeweils $T_0/2$. Die Höhe der Rechtecke beträgt $2\ \rm V$.
Das Signal $v(t)$ am Systemausgang wird als Sinkensignal bezeichnet. Dieses ist für zwei verschiedene Parameterwerte der äquivalenten Impulsdauer in der Grafik dargestellt:
- Das Signal $v_1(t)$ ergibt sich, wenn die äquivalente Impulsdauer von $h(t)$ genau $Δt_1$ ist.
- Entsprechend ergibt sich das Signal $v_2(t)$ mit der äquivalenten Impulsdauer $Δt_2$.
Die Veränderung vom Rechtecksignal $q(t)$ zum dreieck- bzw. trapezförmigen Sinkensignal $v(t)$ ist auf lineare Verzerrungen zurückzuführen und wird durch das Fehlersignal $ε(t) = v(t) – q(t)$ erfasst. Mit den Leistungen $P_q$ und $P_ε$ der Signale $q(t)$ und $ε(t)$ kann das Sinken–SNR berechnet werden:
- $$\rho_{v} =P_{q}/{P_{\varepsilon }} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Qualitätskriterien.
- Bezug genommen wird insbesondere auf die Seite Signal-zu-Stör-Leistungsverhältnis und auf das Kapitel Lineare Verzerrungen im Buch „Lineare zeitinvariante Systeme”.
- Die Leistungen $P_q$ und $P_ε$ sind die quadratischen Mittelwerte der Signale $q(t)$ und $ε(t)$ und können bei periodischen Signalen mit der Periodendauer $T_0$ wie folgt ermittelt werden:
- $$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Die Angabe von Leistungen in $\rm V^2$ bedeutet, dass die Signale auf den Widerstand $R = 1\ \rm \Omega$ bezogen werden.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$\Delta t_1 = T_0 /2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \Delta t_1 / T_0\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
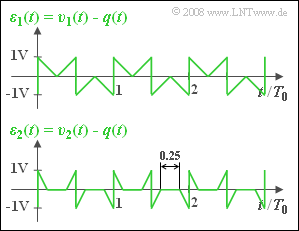
(2) Das Fehlersignal $ε_1(t)$ ist in nebenstehender Grafik oben dargestellt. Man erkennt, dass $ε_1(t)$ alle Werte zwischen $±1 \ \rm V$ annehmen kann:
- $${\varepsilon}_\text{ 1, max} \hspace{0.15cm}\underline {= {1}\;{\rm V}} \hspace{0.05cm}.$$
(3) Es genügt die Mittelung über den Zeitbereich von$t = 0$ bis $t =T_0/4$, da alle anderen Teilintervalle genau gleiche Beiträge liefern:
- $$P_{\varepsilon{\rm 1}} = \frac{1}{T_{\rm 0}/4} \cdot \int_{0}^{ T_{\rm 0}/4} {\varepsilon_1(t)^2 }\hspace{0.1cm}{\rm d}t = \frac{1 \,{\rm V}^2}{T_{\rm 0}/4} \cdot \int_{0}^{ T_{\rm 0}/4} {\left( 1 - \frac{t}{T_{\rm 0}/4}\right)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
Mit der Substitution $x = 4 · t/T_0$ kann hierfür auch geschrieben werden:
- $$P_{\varepsilon{\rm 1}} = 1 \,{\rm V}^2 \cdot \int_{0}^{ 1} {\left( 1 - 2x + x^2\right)}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}= 1 \,{\rm V}^2 \cdot \left( 1 - 1 + \frac{1}{3}\right)\hspace{0.15cm}\underline {= 0.333} \,{\rm V}^2\hspace{0.05cm}.$$
(4) Die Mittelung über eine Periode des quadrierten Quellensignals liefert:
- $$P_{q} = \frac{1}{T_0} \cdot \left[(2\,{\rm V})^2 \cdot \frac{T_0}{2}+(0\,{\rm V})^2 \cdot \frac{T_0}{2} \right]\hspace{0.15cm}\underline {= 2\,{\rm V^2}}\hspace{0.05cm}.$$
Das Sinken–SNR beträgt somit
- $$\rho_{v{\rm 1}} = \frac{P_{q}}{P_{\varepsilon {\rm 1}}} = \frac{2 \,{\rm V}^2}{0.333 \,{\rm V}^2}\hspace{0.15cm}\underline {= 6} \hspace{0.05cm}.$$
(5) Entsprechend der Skizze auf dem Angabenblatt wird nun aus einem Rechteck der Dauer $0.5 \cdot T_0$ ein Trapez der absoluten Dauer $0.75 · T_0$. Damit ist nach den Gesetzen der Faltung offensichtlich, dass die äquivalente Impulsdauer $Δt_2/T_0\hspace{0.15cm}\underline { = 0.25}$ sein muss.
(6) Die untere Skizze in obiger Grafik zeigt, dass sich $ε_2(t)$ ebenso wie $ε_1(t)$ innerhalb einer Periodendauer $T_0$ aus vier Dreiecken zusammensetzt, doch sind diese nur halb so breit. In der Hälfte der Zeit ist nämlich $ε_2(t) = 0$.
Wegen $ε_\text{2, max} = ε_\text{1, max} = 1 \ \rm V$ erhält man:
- $$P_{\varepsilon{\rm 2}} ={P_{\varepsilon{\rm 1}}}/{2} \hspace{0.15cm}\underline {= 0.167} \,{\rm V}^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 2}} = {P_{q}}/{P_{\varepsilon {\rm 2}}}\hspace{0.15cm}\underline {= 12} \hspace{0.05cm}.$$
(7) Für $Δt = T_0/2$ wurde in der Teilaufgabe (3) die Verzerrungsleistung $P_{ε1} = 1/3 \ \rm V^{ 2 }$ berechnet. In der Teilaufgabe(6) wurde gezeigt, dass bei $Δt = T_0/4$ die Verzerrungsleistung $P_{ε2}$ nur halb so groß ist.
Anschaulich wurde erläutert, dass ein linearer Zusammenhang besteht. Daraus folgen für $Δt ≤ T_0/2$ die empirischen Gleichungen:
- $$P_{\varepsilon} = \frac{2 \,{\rm V}^2}{3} \cdot \frac{\Delta t}{T_0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} = \frac{P_{q}}{P_{\varepsilon }}= \frac{3}{\Delta t/T_0} \hspace{0.05cm}.$$
Der Sonderfall $Δt = T_0/20$ führt somit zu den Resultaten:
- $$P_{\varepsilon{\rm 3}} = \frac{2 \,{\rm V}^2}{60} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 3}} = \frac{P_{q}}{P_{\varepsilon {\rm 3}}}\hspace{0.15cm}\underline {= 60} \hspace{0.05cm}.$$