Aufgaben:Aufgabe 1.2Z: 3D–Darstellung von Codes: Unterschied zwischen den Versionen
Aus LNTwww
Wael (Diskussion | Beiträge) |
Wael (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID2400__KC_Z_1_2.png|right|]] |
| + | Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im ''n''–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge ''n'' = 3: | ||
| + | :$$\underline{x} \hspace{-0.15cm} = \hspace{-0.15cm} (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\\ x_i \hspace{-0.15cm} \in \hspace{-0.15cm} \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$ | ||
| + | Allgemein gilt bei der Blockcodierung: | ||
| + | *Das Informationswort <u>u</u> = (u_{1}, u_{2}, ... , u_{k}) wird eindeutig in das Codewort <u>x</u> = (x_{1}, x_{2}, ... , x_{n}) überführt. | ||
| + | *Die Coderate beträgt R = k/n. | ||
| + | *Die Hamming–Distanz $d_{\rm H}$(<u>x</u>,<u> x'</u>) zwischen zwei Codeworten <u>x</u> ∈ C und <u>x'</u> ∈ C gibt die Anzahl der Bitpositionen an, in denen sich x und x' unterscheiden. | ||
| + | *Die Minimaldistanz $d_{\rm min}$ = min [$d_{\rm H}$(<u>x</u>,<u> x'</u>)] ist ein Maß für die Korrekturfähigkeit eines Codes. | ||
| + | *Es können e =$d_{\rm min}$ – 1 Fehler erkannt und t = ($d_{\rm min}$ – 1)/2 korrigiert werden. Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$ . | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 23. November 2017, 21:33 Uhr
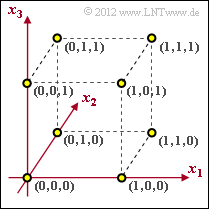
Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im n–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge n = 3:
- $$\underline{x} \hspace{-0.15cm} = \hspace{-0.15cm} (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\\ x_i \hspace{-0.15cm} \in \hspace{-0.15cm} \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$
Allgemein gilt bei der Blockcodierung:
- Das Informationswort u = (u_{1}, u_{2}, ... , u_{k}) wird eindeutig in das Codewort x = (x_{1}, x_{2}, ... , x_{n}) überführt.
- Die Coderate beträgt R = k/n.
- Die Hamming–Distanz $d_{\rm H}$(x, x') zwischen zwei Codeworten x ∈ C und x' ∈ C gibt die Anzahl der Bitpositionen an, in denen sich x und x' unterscheiden.
- Die Minimaldistanz $d_{\rm min}$ = min [$d_{\rm H}$(x, x')] ist ein Maß für die Korrekturfähigkeit eines Codes.
- Es können e =$d_{\rm min}$ – 1 Fehler erkannt und t = ($d_{\rm min}$ – 1)/2 korrigiert werden. Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$ .
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.