Aufgaben:Aufgabe 1.17: Zum Kanalcodierungstheorem: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
Wael (Diskussion | Beiträge) |
||
| Zeile 31: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welche der roten Punkte gehören zu welchem Hamming–Code? ''Hinweis:'' Die Grafik wurde für BER $= 10^{–5}$ erstellt. |
|type="[]"} | |type="[]"} | ||
| − | - | + | + ${\boldsymbol{\rm X}}$ bezeichnet den (7, 4, 3)–Hamming–Code. |
| − | + | + | + ${\boldsymbol{\rm Y}}$ bezeichnet den (15, 11, 3)–Hamming–Code. |
| + | + ${\boldsymbol{\rm Z}\$ bezeichnet den (31, 15, 3)–Hamming–Code. | ||
| + | |||
| + | {In welche Richtung werden sich die Punkte ${\boldsymbol{\rm X}}$, ${\boldsymbol{\rm Y}}$ und ${\boldsymbol{\rm Z}}$ verschieben, wenn die Grafik für BER $= 10^{–10}$ erstellt werden soll? | ||
| + | |type="[]"} | ||
| + | - Nach links, | ||
| + | + nach rechts, | ||
| + | - nach oben. | ||
| − | { | + | {Bis zu welcher Coderate $R_{\rm max}$ könnte man ein System mit gleichem $E_{\rm B}/N_{0}$ wie System ${\boldsymbol{\rm W}}$ betreiben? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\ E_{\rm B}/N_{0} = 3 \ {\rm dB}: \ \ \ R_{\rm max}$ = { 0.84 3% } |
| + | |||
| + | {Um welchen Faktor ''A'' könnte die Sendeleistung von System ${\boldsymbol{\rm W}}$ entsprechend der Kanalkapazitätskurve ''C'' herabgesetzt werden? | ||
| + | |type="{}"} | ||
| + | $\ R = 0.5: \ \ \ A ({\rm größer} 1!)$ = { 1.94 3% } | ||
Version vom 14. Dezember 2017, 16:12 Uhr
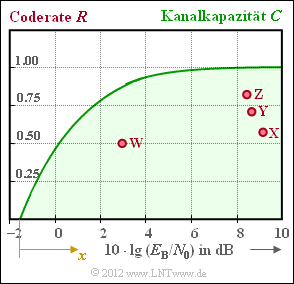
Die Grafik zeigt maximal zulässige Coderaten $R < C$ gemäß Shannons Kanalcodierungstheorem:
- Die grüne Grenzkurve gibt die Kanalkapazität C für den AWGN–Kanal unter der Voraussetzung eines binären Eingangssignals („BPSK”) an.
- In Aufgabe 1.17Z wird hierfür eine einfache Näherung angegeben. Mit der zweiten Abszisse
- $$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$
ergibt sich näherungsweise:
- $$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm exp}(- 0.4 \cdot x) \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm}} x > 0, \\ \\{\rm f\ddot{u}r\hspace{0.15cm}} x < 0. \end{array}$$
- Gilt $R < C$, so kann ein Code gefunden werden, der bei unendlich langen Blöcken $(n → ∞)$ zur Fehlerwahrscheinlichkeit 0 führt. Wie dieser Code aussieht, ist durch das Kanalcodierungstheorem nicht festgelegt und spielt für diese Aufgabe auch keine Rolle.
In die Grafik eingezeichnet sind die Kenngrößen etablierter Codiersysteme. Die roten Punkte $\color{red}{\boldsymbol{\rm X}}$, $\color{red}{\boldsymbol{\rm Y}}$ und $\color{red}{\boldsymbol{\rm Z}}$ markieren drei Hamming–Codes unterschiedlicher Codelängen, nämlich mit $n = 7$, $n = 15$ und $n = 31$. Das Codiersystem $\color{red}{\boldsymbol{\rm W}}$ ist durch die Kenngrößen $R = 0.5$ und $10 \ · \ {\rm lg} E_{\rm B}/N_{0} = 3 {\rm dB}$ gekennzeichnet.
Hinweis:
Die Aufgabe gehört zum Themengebiet von Kapitel Informationstheoretische Grenzen der Kanalcodierung. Die informationstheoretische Grenze „Kanalkapazität” bezieht sich auf die Fehlerwahrscheinlichkeit 0. Die eingezeichneten Punkte realer Übertragungssysteme ergeben sich dagegen unter der Annahme BER $= 10^{–5}$.
Fragebogen
Musterlösung