Aufgaben:Aufgabe 1.17: Zum Kanalcodierungstheorem: Unterschied zwischen den Versionen
Aus LNTwww
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
}} | }} | ||
| − | [[Datei:P_ID2412__KC_A_1_16.png|right|frame|Kanalkapazität und Coderaten etablierter Systeme]] | + | [[Datei:P_ID2412__KC_A_1_16.png|right|frame|Kanalkapazität (grün) und Coderaten (rote Punkte) einiger etablierter Systeme]] |
| − | Die Grafik zeigt maximal zulässige | + | Die Grafik zeigt die maximal zulässige Coderate $R < C$ gemäß Shannons [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalcodierungstheorem_und_Kanalkapazit.C3.A4t|Kanalcodierungstheorem]]: |
| − | *Die grüne Grenzkurve gibt die Kanalkapazität $C$ für den AWGN–Kanal unter der Voraussetzung eines binären Eingangssignals („BPSK”) an. | + | *Die grüne Grenzkurve gibt die Kanalkapazität $C$ für den AWGN–Kanal unter der Voraussetzung eines binären Eingangssignals („BPSK”) an. |
| − | *In [[Aufgaben:1.17Z_BPSK–Kanalkapazität|Aufgabe 1.17Z]] wird hierfür eine einfache Näherung angegeben. Mit der zweiten Abszisse | + | *In der [[Aufgaben:1.17Z_BPSK–Kanalkapazität|Aufgabe 1.17Z]] wird hierfür eine einfache Näherung angegeben. Mit der zweiten Abszisse |
:$$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$ | :$$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$ | ||
| − | ergibt sich näherungsweise: | + | :ergibt sich näherungsweise: |
| − | :$$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm | + | :$$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm}} x > 0, \\ \\{\rm f\ddot{u}r\hspace{0.15cm}} x < 0. \end{array}$$ |
| − | *Gilt $R < C$, so kann ein Code gefunden werden, der bei unendlich langen Blöcken $(n → ∞)$ zur Fehlerwahrscheinlichkeit | + | *Gilt $R < C$, so kann ein Code gefunden werden, der bei unendlich langen Blöcken $(n → ∞)$ zur Fehlerwahrscheinlichkeit „Null” führt. |
| + | *Wie dieser Code aussieht, ist durch das Kanalcodierungstheorem nicht festgelegt und spielt für diese Aufgabe auch keine Rolle. | ||
| + | |||
| + | |||
| + | In die Grafik als Punkte eingezeichnet sind die Kenngrößen etablierter Codiersysteme: | ||
| + | *Die Punkte $\rm X$, $\rm Y$ und $\rm Z$ markieren drei Hamming–Codes unterschiedlicher Codelängen, nämlich mit $n = 7$, $n = 15$ und $n = 31$. | ||
| + | |||
| + | *Das Codiersystem $\rm W$ ist durch die Kenngrößen $R = 0.5$ und $10 \ · \ \lg {E_{\rm B}/N_0} = 3 {\rm dB}$ gekennzeichnet. | ||
| − | |||
| − | + | ||
| − | *Die Aufgabe gehört zum Themengebiet von Kapitel [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung|Informationstheoretische Grenzen der Kanalcodierung]]. | + | |
| − | * Die informationstheoretische Grenze | + | Hinweise: |
| − | + | *Die Aufgabe gehört zum Themengebiet von Kapitel [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung|"Informationstheoretische Grenzen der Kanalcodierung"]]. | |
| + | |||
| + | * Die informationstheoretische Grenze "Kanalkapazität" bezieht sich auf die Fehlerwahrscheinlichkeit $\rm BER =0$. | ||
| + | |||
| + | *Die eingezeichneten Punkte realer Übertragungssysteme ergeben sich dagegen unter der Annahme $\rm BER = 10^{–5}$. | ||
| + | |||
| Zeile 35: | Zeile 46: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der | + | {Welche der Punkte gehören zu welchem Hamming–Code? Hinweis: Die Grafik wurde für $\rm BER = 10^{–5}$ erstellt. |
|type="[]"} | |type="[]"} | ||
| − | + $ | + | + $\rm X$ bezeichnet den $(7, 4, 3)$–Hamming–Code. |
| − | + $ | + | + $\rm Y$ bezeichnet den $(15, 11, 3)$–Hamming–Code. |
| − | + $ | + | + $\rm Z$ bezeichnet den $(31, 26, 3)$–Hamming–Code. |
| − | {In welche Richtung werden sich die Punkte $ | + | {In welche Richtung(en) werden sich die Punkte $\rm X$, $\rm Y$ und $\rm Z$ verschieben, wenn die Grafik für $\rm BER = 10^{–10}$ erstellt werden soll? |
|type="[]"} | |type="[]"} | ||
- Nach links, | - Nach links, | ||
| Zeile 47: | Zeile 58: | ||
- nach oben. | - nach oben. | ||
| − | {Bis zu welcher Coderate $R_{\rm max}$ könnte man ein System mit gleichem $E_{\rm B}/N_{0}$ wie System | + | {Bis zu welcher Coderate $R_{\rm max}$ könnte man ein System mit gleichem $E_{\rm B}/N_{0} = 3 \ {\rm dB}$ wie System $\rm W$ betreiben? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $R_{\rm max} \ = \ $ { 0.84 3% } |
| − | {Um welchen Faktor $A$ könnte die Sendeleistung von System | + | {Um welchen Faktor $A > 1$ könnte die Sendeleistung von System $\rm W$ nach der Kanalkapazitätskurve mit $ R = 0.5$ herabgesetzt werden? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A \ = \ $ { 1.94 3% } |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig sind <u>alle Lösungsvorschläge</u> | + | '''(1)''' Richtig sind <u>alle Lösungsvorschläge</u>: |
| + | *Aus der Grafik erkennt man bereits, dass die Rate von $\rm Z$ größer ist als die Rate von $\rm Y$ und die Rate von $\rm Y$ größer ist als die Rate von $\rm X$. | ||
| + | |||
| + | *Die tatsächlichen Raten dieser drei Systeme sind $R_{\rm X} = 4/7 = 0.571$, $R_{\rm Y} = 11/15 = 0.733$ und $R_{\rm Z} = 26/31 = 0.839$. | ||
| + | *Da zudem der $(31, 26, 3)$–Hamming–Code ⇒ Code $\rm Z$ die größte Codewortlänge $n$ aufweist, benötigt er trotz größerer Coderate $R$ für ${\rm BER} = 10^{–5}$ ein geringeres $E_{\rm B}/N_{0}$ als die beiden anderen Hamming–Codes. | ||
| − | |||
| − | '''( | + | '''(2)''' Richtig ist <u>die Antwort 2</u>: |
| + | *Für eine kleinere Bitfehlerrate benötigt man stets ein größeres $E_{\rm B}/N_{0}$. | ||
| − | + | *Eine vertikale Verschiebung gibt es nicht, da sich auch mit $\rm BER = 10^{–10}$ an den Coderaten nichts ändert. | |
| + | |||
| − | '''( | + | '''(3)''' Für den logarithmierten AWGN–Parameter $10 · \lg {E_{\rm B}/N_0} = 3 \ {\rm dB}$ ergibt sich die vorne angegebene Hilfsgröße $x = 1.6 + 3 = 4.6.$ Damit erhält man: |
| − | :$$1 - {\rm | + | |
| + | :$$R_{\rm max} = C (x = 4.6)= 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} 4.6} \hspace{0.15cm} \underline{= 0.84} \hspace{0.05cm}.$$ | ||
| + | |||
| − | |||
| − | $10 | + | '''(4)''' Entsprechend der vorgegebenen Gleichung gilt nun: |
| + | :$$1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = \frac{-{\rm ln}(0.5)}{-0.4} = 1.73\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | + | *$10 · \lg {E_{\rm B}/N_0}$ könnte demnach um $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$ herabgesetzt werden, also um den Faktor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$ | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Kanalcodierung|^1.7 Informationstheoretische Grenzen | + | [[Category:Aufgaben zu Kanalcodierung|^1.7 Informationstheoretische Grenzen^]] |
Aktuelle Version vom 28. September 2022, 16:40 Uhr
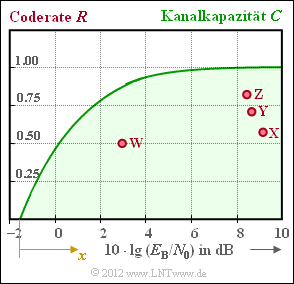
Die Grafik zeigt die maximal zulässige Coderate $R < C$ gemäß Shannons Kanalcodierungstheorem:
- Die grüne Grenzkurve gibt die Kanalkapazität $C$ für den AWGN–Kanal unter der Voraussetzung eines binären Eingangssignals („BPSK”) an.
- In der Aufgabe 1.17Z wird hierfür eine einfache Näherung angegeben. Mit der zweiten Abszisse
- $$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$
- ergibt sich näherungsweise:
- $$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm}} x > 0, \\ \\{\rm f\ddot{u}r\hspace{0.15cm}} x < 0. \end{array}$$
- Gilt $R < C$, so kann ein Code gefunden werden, der bei unendlich langen Blöcken $(n → ∞)$ zur Fehlerwahrscheinlichkeit „Null” führt.
- Wie dieser Code aussieht, ist durch das Kanalcodierungstheorem nicht festgelegt und spielt für diese Aufgabe auch keine Rolle.
In die Grafik als Punkte eingezeichnet sind die Kenngrößen etablierter Codiersysteme:
- Die Punkte $\rm X$, $\rm Y$ und $\rm Z$ markieren drei Hamming–Codes unterschiedlicher Codelängen, nämlich mit $n = 7$, $n = 15$ und $n = 31$.
- Das Codiersystem $\rm W$ ist durch die Kenngrößen $R = 0.5$ und $10 \ · \ \lg {E_{\rm B}/N_0} = 3 {\rm dB}$ gekennzeichnet.
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Kapitel "Informationstheoretische Grenzen der Kanalcodierung".
- Die informationstheoretische Grenze "Kanalkapazität" bezieht sich auf die Fehlerwahrscheinlichkeit $\rm BER =0$.
- Die eingezeichneten Punkte realer Übertragungssysteme ergeben sich dagegen unter der Annahme $\rm BER = 10^{–5}$.
Fragebogen
Musterlösung
(1) Richtig sind alle Lösungsvorschläge:
- Aus der Grafik erkennt man bereits, dass die Rate von $\rm Z$ größer ist als die Rate von $\rm Y$ und die Rate von $\rm Y$ größer ist als die Rate von $\rm X$.
- Die tatsächlichen Raten dieser drei Systeme sind $R_{\rm X} = 4/7 = 0.571$, $R_{\rm Y} = 11/15 = 0.733$ und $R_{\rm Z} = 26/31 = 0.839$.
- Da zudem der $(31, 26, 3)$–Hamming–Code ⇒ Code $\rm Z$ die größte Codewortlänge $n$ aufweist, benötigt er trotz größerer Coderate $R$ für ${\rm BER} = 10^{–5}$ ein geringeres $E_{\rm B}/N_{0}$ als die beiden anderen Hamming–Codes.
(2) Richtig ist die Antwort 2:
- Für eine kleinere Bitfehlerrate benötigt man stets ein größeres $E_{\rm B}/N_{0}$.
- Eine vertikale Verschiebung gibt es nicht, da sich auch mit $\rm BER = 10^{–10}$ an den Coderaten nichts ändert.
(3) Für den logarithmierten AWGN–Parameter $10 · \lg {E_{\rm B}/N_0} = 3 \ {\rm dB}$ ergibt sich die vorne angegebene Hilfsgröße $x = 1.6 + 3 = 4.6.$ Damit erhält man:
- $$R_{\rm max} = C (x = 4.6)= 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} 4.6} \hspace{0.15cm} \underline{= 0.84} \hspace{0.05cm}.$$
(4) Entsprechend der vorgegebenen Gleichung gilt nun:
- $$1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = \frac{-{\rm ln}(0.5)}{-0.4} = 1.73\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$
- $10 · \lg {E_{\rm B}/N_0}$ könnte demnach um $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$ herabgesetzt werden, also um den Faktor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$