Aufgabe 1.12Z: Vergleich von HC (7, 4, 3) und HC (8, 4, 4)

Blockfehlerwahrscheinlichkeit von (7, 4, 3)– und (8, 4, 4)–Code

Nun sollen die Blockfehlerwahrscheinlichkeiten

des (7, 4, 3)–Hamming–Codes und
des erweiterten (8, 4, 4)–Hamming–Codes

miteinander verglichen werden. Zugrunde gelegt werden

das BSC–Kanalmodell (Parameter $\varepsilon$, insbesondere $\varepsilon = 0.01$ für numerische Ergebnisse),
die Syndromdecodierung, mit der bei beiden Codes eine Maximum–Likelihood–Detektion realisiert wird. Bei richtiger Belegung der Syndromtabelle ergibt sich jeweils die minimale Blockfehlerwahrscheinlichkeit.

Für den (7, 4, 3)–Code wurde in der Aufgabe 1.12 berechnet:

$${\rm Pr(Blockfehler)} = 1 - (1 - \varepsilon)^7 - 7 \cdot \varepsilon \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$

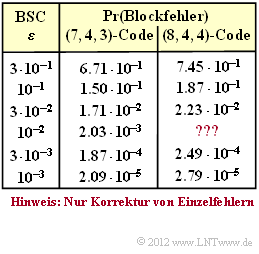
Die Zahlenwerte sind in der Spalte 2 der obigen Tabelle angegeben. Es handelt sich um die tatsächlichen Werte, also nicht um die in Aufgabe 1.12 hergeleitete Näherung: ${\rm Pr(Blockfehler)} \approx 21 \cdot \varepsilon^2$.

Anzumerken ist, dass aufgrund des BSC–Kanalmodells nur harte Entscheidungen möglich sind. Mit Soft–Decision ergeben sich etwas kleinere Blockfehlerwahrscheinlichkeiten.

Nun soll die Blockfehlerwahrscheinlichkeit für den erweiterten (8, 4, 4)–Code ermittelt werden:

Die Berechnung in Teilaufgabe 4) erfolgt unter der Maßgabe, dass wie beim (7, 4, 3)–Code nur die Fehlermuster mit einer einzigen „1” korrigiert werden. In der rechten Spalte obiger Tabelle sind die Ergebnisse eingetragen, bis auf den Wert für $\varepsilon = 0.01$, der explizit berechnet werden soll.

In der Teilaufgabe 5) soll dagegen berücksichtigt werden, dass beim erweitereten (8, 4, 4)–Code Teile der Syndromtabelle noch mit Gewicht–2–Fehlermustern aufgefüllt werden können.

Hinweis:

Die Aufgabe bezieht sich auf Kapitel Decodierung linearer Blockcodes. Von Interesse für die Lösung dieser Aufgabe ist insbesondere die Seite Verallgemeinerung der Syndromdecodierung (2).

Fragebogen

$\ (7, 4, 3)–Code: \ \ \ \ N_{\rm ges} \ = \ $

$\ (8, 4, 4)–Code: \ \ \ \ N_{\rm ges} \ = \ $

$\ (7, 4, 3)–Code: \ \ \ \ N_{2} ' \ = \ $

$\ (8, 4, 4)–Code: \ \ \ \ N_{2} ' \ = \ $

$\ (7, 4, 3)–Code: \ \ \ \ N_{2} \ = \ $

$\ (8, 4, 4)–Code: \ \ \ \ N_{2} \ = \ $

$\ {\rm Pr(Blockfehler)} \ = \ $

$\ \cdot 10^{-3}$

$\ {\rm Pr(Blockfehler)} \ = \ $

$\ \cdot 10^{-3}$

Musterlösung

(1) Die Größe der Syndromtabelle ist allgemein $N_{\rm ges} = 2m; m = n – k$ gibt die Anzahl der Prüfbits an.

Beim (7, 4, 3)–Hamming–Code ist $m = n – k = 3$ ⇒ die Länge der Tabelle ist $N_{\rm ges} \underline{= 8}.$
Die Syndromtabelle des (8, 4, 4)–Codes ist doppelt so groß: $N_{\rm ges} = 2^4 \underline{= 16}$.

(2) Allgemein gilt für die Anzahl der Einträge mit Gewicht–2–Fehlermustern: $N_{2}′ = „ n {\rm über} 2”$. Daraus ergeben sich die Zahlenwerte

$N_{2}′ \ \underline{= 21}$ für $n = 7$ ⇒ (7, 4, 3)–Code,
$N_{2}′ \ \underline{= 28}$ für $n = 8$ ⇒ (8, 4, 4)–Code.

(3) Beim (7, 4, 3)–Hamming–Code ist die Syndromtabelle gefüllt mit einem Eintrag für den fehlerfreien Fall $(N_{0}= 1)$ und $n = 7$ Einträge mit Gewicht–1–Fehlermustern $(N_{1} = 7)$. Damit ist die Anzahl der Einträge mit Gewicht–2–Fehlermustern gleich

$$N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 0} \hspace{0.05cm}.$$

Dagegen gilt für den erweiterten (8, 4, 4)–Hamming–Code:

$$N_0 = 1\hspace{0.05cm},\hspace{0.2cm}N_1 = 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 7} \hspace{0.05cm}.$$

(4) Analog zur Musterlösung der Aufgabe 1.12 (1) und (2) erhält man hier:

$${\hspace{-4.3cm}\rm Pr(Blockfehler)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - (1 - \varepsilon)^8 - 8 \cdot \varepsilon \cdot (1 - \varepsilon)^7=\\ \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - 0.922745 - 0.074655\hspace{0.15cm} \underline{= 2.69 \cdot 10^{-3}} \hspace{0.05cm}.$$

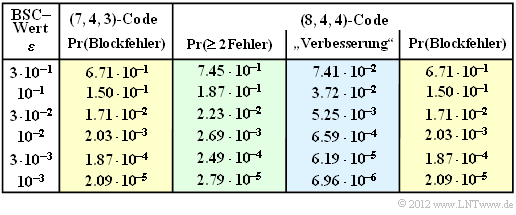
In der Tabelle sind für diesen Fall und für verschiedene BSC–Parameter ε die Ergebnisse in der grün hinterlegten Spalte eingetragen. Gegenüber dem (7, 4, 3)–Code ergibt sich stets eine Verschlechterung.

Blockfehlerwahrscheinlichkeit von (7, 4, 3)– und (8, 4, 4)–Code

(5) Bei bestmöglicher Korrektur (gefüllte Syndromtabelle) werden auch sieben Gewicht–2–Fehlermuster korrigiert. Damit vermindert sich die Blockfehlerwahrscheinlichkeit um

$${\rm Pr(Gewicht\hspace{-0.1cm}-\hspace{-0.1cm}2\hspace{-0.1cm}-\hspace{-0.1cm}Fehlermuster\hspace{0.15cm} wird \hspace{0.15cm} korrigiert)} = 7 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$

Für $\varepsilon = 0.01$ macht diese „Verbesserung” etwa $0.66 · 10^{–3}$ aus. Die Blockfehlerwahrscheinlichkeit ergibt sich somit zu

$${\rm Pr(Blockfehler)} = 2.69 \cdot 10^{-3} - 0.66 \cdot 10^{-3} \underline{= 2.03 \cdot 10^{-3}} \hspace{0.05cm}.$$

In der obigen Tabelle ist diese Rechnung für verschiedene BSC–Parameter $\varepsilon$ durchgeführt. Man erkennt: Die Blockfehlerwahrscheinlichkeit des erweiterten (8, 4, 4)–Hamming–Codes (siehe letzte Spalte) stimmt exakt mit der des (7, 4, 3)–Hamming–Codes (Spalte 2) überein. Die Korrektur von 25% der Gewicht–2–Fehlermuster gleicht genau die Tatsache aus, dass beim (8, 4, 4)–Code Fehlermuster mit mehr als einem Fehler (Spalte 3) wahrscheinlicher sind als beim (7, 4, 3)–Code (Spalte 2).