Aufgaben:Aufgabe 1.08: Identische Codes

• Zurück zum Buch

Zuordnung des betrachteten (6, 3)–Blockcodes

Wir betrachten einen Blockcode $C$, der durch folgende Generatormatrix beschrieben wird:

$${ \boldsymbol{\rm G}} = \begin{pmatrix} 0 &0 &1 &0 &1 &1\\ 1 &0 &0 &1 &1 &0\\ 0 &1 &1 &1 &1 &0 \end{pmatrix} \hspace{0.05cm}.$$

Die Zuordnung zwischen den Informationsworten $\underline{u}$ und den Codeworten $\underline{x}$ kann der beiliegenden Tabelle entnommen werden. Man erkennt, dass es sich dabei nicht um einen systematischen Code handelt.

Durch Manipulation der Generatormatrix $\boldsymbol {\rm G}$ lassen sich daraus identische Codes konstruieren. Darunter versteht man Codes mit gleichen Codeworten, jedoch unterschiedlicher Zuordnung $\underline{u} \rightarrow \underline{u}$. Folgende Operationen sind erlaubt, um einen identischen Code zu erhalten:

• Vertauschen oder Permutieren der Zeilen,
• Multiplizieren aller Zeilen mit einem konstanten Vektor ungleich $0$,
• Ersetzen einer Zeile durch eine Linearkombination zwischen dieser Zeile und einer anderen.

Für den in der Teilaufgabe 3) gesuchten Code $C_{\rm sys} \Rightarrow$ Generatormatrix $\boldsymbol{\rm G}_{\rm sys}$ wird weiter gefordert, dass er systematisch ist.

Hinweis :

Die Aufgabe bezieht sich vorwiegend auf die Seite Systematische Codes im Kapitel Allgemeine Beschreibung linearer Blockcodes1.4. Bezug genommen wird zudem auf die so genannte Singleton–Schranke. Diese besagt, dass die minimale Hamming–Distanz eines $(n, k)$–Blockcodes nach oben beschränkt ist:

$$d_{\rm min} \le n - k +1.$$

Fragebogen

1

Geben Sie die Kenngrößen des gegebenen Codes $C$ an.

$n \ = \ $

$k \ = \ $

$|C| \ = \ $

$R \ = \ $

$m \ = \ $

$d_{\rm min}$ =

2

Gibt es einen (6, 3)–Blockcode mit größerer Minimaldistanz?

	Ja.
	Nein.

3

Wie lautet die Generatormatrix ${\boldsymbol{\rm G}}_{\rm sys}$ des identischen systematischen Codes?

	Die 1. Zeile lautet $„1 \ 0 \ 1 \ 1 \ 0 \ 1”$.
	Die 2. Zeile lautet $„0 \ 1 \ 0 \ 1 \ 0 \ 1”$.
	Die 3. Zeile lautet $„0 \ 0 \ 1 \ 0 \ 1 \ 1”$.

4

Welche Zuordnungen ergeben sich bei dieser Codierung?

	$\underline{u} = (0, 0, 0) \Rightarrow \underline{x}_{\rm sys} = (0, 0, 0, 0, 0, 0)$.
	$\underline{u} = (0, 0, 1) \Rightarrow \underline{x}_{\rm sys}= (0, 0, 1, 0, 0, 1)$.
	$\underline{u} = (0, 1, 0) \Rightarrow \underline{x}_{\rm sys} = (0, 1, 0, 1, 1, 0)$.

5

Welche Prüfbits hat der systematische Code $\underline{x}_{\rm sys} = (u_{1}, u_{2}, u_{3}, p_{1}, p_{2}, p_{3})$?

	$p_{1} = u_{1} \oplus u_{2},$
	$p_{2} = u_{2} \oplus u_{3},$
	$p_{3} = u_{1} \oplus u_{3}.$

Musterlösung

Musterlösung

(1)  Der vorgegebene Code $C$ wird durch folgende Kenngrößen charakterisiert:

• Bitanzahl der Codeworte: $\underline{n = 6}$,
• Bitanzahl der Informationsworte: $\underline{k = 3}$,
• Anzahl der Codeworte (Codeumfang): $|C| = 2^k \Rightarrow \underline{|C| = 8}$,
• Coderate: $R = k/n = 3/6 \Rightarrow \underline{R = 1/2}$,
• Anzahl der Prüfbitgleichungen: $\underline{m = n – k = 3}$,
• minimale Hamming–Distanz (siehe Tabelle): $\underline{d}_{\rm min} \underline{= 3}$.

(2)  Nach der Singleton–Schranke gilt $d_{\rm min} ≤ n – k + 1$. Mit $n = 6$ und $k = 3$ erhält man hierfür $d_{\rm min} ≤ 4$. Es kann also durchaus ein (6, 3)–Blockcode mit größerer Minimaldistanz konstruiert werden $\Rightarrow \underline{\rm JA}$. Wie ein solcher Code aussieht, wurde freundlicherweise nicht gefragt.

Die Minimaldistanz aller Hamming–Codes ist $d_{\rm min} = 3$, und nur der Sonderfall mit $n = 3$ und $k = 1$ erreicht den Grenzwert. Dagegen erreichen das Maximum entsprechend der Singleton–Schranke:

• alle Wiederholungscodes (Repetition Codes, RC) wegen $k = 1$und $d_{\rm min} = n$; hierzu gehört auch der (3, 1)–Hamming–Code, der ja bekannterweise identisch ist mit RC (3, 1),

• alle Single Parity–check Codes (SPC): $k = n – 1, d_{\rm min} = 2$.

(3)  Vertauscht man Zeilen in der Generatormatrix $\boldsymbol {\rm G}$, so kommt man zu einem identischen Code $C'$. Das heißt: Die Codes $C$ und $C'$ beinhalten die genau gleichen Codeworte. Beispielsweise erhält man nach zyklischem Zeilentausch $2 \rightarrow 1, 3 \rightarrow 2$ und $1 \rightarrow 3$ die neue Matrix

$${ \boldsymbol{\rm G}}' = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &1 &1 &1 &0\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$

Die erste und die letzte Zeile der neuen Matrix entsprechen schon den Vorgaben eines systematischen Codes, nämlich, dass deren Generatormatrix ${ \boldsymbol{\rm G}_{\rm sys}}$ mit einer Diagonalmatrix beginnen muss. Ersetzt man die Zeile 2 durch die Modulo–2–Summe von Zeile 2 und 3, so erhält man:

$${ \boldsymbol{\rm G}}_{\rm sys} = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &0 &1 &0 &1\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$

Auch dieser systematische Code beinhaltet genau die gleichen Codeworte wie die Codes $C$ und $C'$. Richtig sind die Lösungsvorschläge 2 und 3.

(4)  Wendet man die Gleichung $\underline{x}_{\rm sys} = \underline{u} \cdot \boldsymbol{\rm G}_{\rm sys}$ auf die obigen Beispiele an, so erkennt man, dass die beiden ersten Aussagen richtig sind, nicht aber die letzte. Ohne Rechnung kommt man zum gleichen Ergebnis, wenn man berücksichtigt, dass

• das systematische Codewort $\underline{x}_{\rm sys}$ mit $\underline{u}$ beginnen muss,
• der Code $C_{\rm sys}$ die gleichen Codeworte beinhaltet wie der vorgegebene Code C.

Für $\underline{u} = (0, 1, 0)$ lautet somit das Codewort $(0, 1, 0, ?, ?, ?)$. Ein Vergleich mit der Codetabelle von $C$ auf der Angabenseite führt zum Ergebnis $\underline{x}_{\rm sys} = (0, 1, 0, 1, 0, 1)$.

(5)  Bei systematischer Codierung besteht folgender Zusammenhang zwischen Generator– und Prüfmatrix:

$${ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_k \: ; \:{ \boldsymbol{\rm P}} \right) \hspace{0.3cm}\Leftrightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} =\left({ \boldsymbol{\rm P}}^{\rm T}\: ; \:{ \boldsymbol{\rm I}}_m \right) \hspace{0.05cm}.$$

Angewendet auf das aktuelle Beispiel erhält man so:

$${ \boldsymbol{\rm G}}_{\rm sys} = \begin{pmatrix} 1 &0 &0 &1 &1 &0\\ 0 &1 &0 &1 &0 &1\\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{\rm sys} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

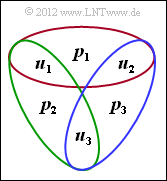
Daraus ergeben sich Prüfgleichungen (siehe Grafik):

Schaubild der Prüfgleichungen

$$Formel: u_1 \oplus u_2 \oplus p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm}0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p_1 = u_1 \oplus u_2 \hspace{0.05cm},\\ u_1 \oplus u_3 \oplus p_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p_2 = u_1 \oplus u_3 \hspace{0.05cm},\\ u_2 \oplus u_3 \oplus p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p_3 = u_2 \oplus u_3 \hspace{0.05cm}.$$

$\Rightarrow$ Richtig ist nur die Aussage 1. Die Angaben für $p_{2}$ und $p_{3}$ sind dagegen genau vertauscht.