Aufgabe 3.5: Kullback-Leibler-Distanz & Binominalverteilung

• Zurück zum Buch

Vorgegebene Wahrscheinlichkeiten

Wir gehen hier von der Binomialverteilung aus, die durch die Parameter  $I$ und  $p$ gekennzeichnet ist   ⇒   siehe Buch „Stochastische Signaltheorie”:

• Wertebereich:

$$X = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 2\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.1cm} ,\hspace{0.05cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.05cm} I\hspace{0.05cm}\}\hspace{0.05cm},$$

• Wahrscheinlichkeiten:

$$P_X (X = \mu) = {I \choose \mu} \cdot p^{\mu} \cdot (1-p)^{I-\mu} \hspace{0.05cm},$$

• linearer Mittelwert:

$$m_X = I \cdot p \hspace{0.05cm},$$

• Varianz:

$$\sigma_X^2 = I \cdot p \cdot (1-p)\hspace{0.05cm}.$$

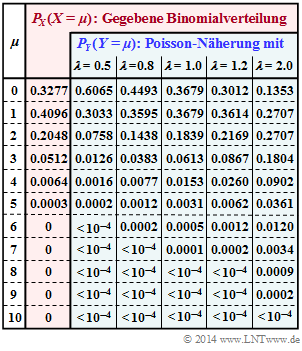
Im rot hinterlegten Teil der Tabelle sind die Wahrscheinlichkeiten $P_X(X = \mu$) der betrachteten Binomialverteilung angegeben. In der Teilaufgabe (1) sollen Sie die dazugehörigen Verteilungsparameter  $I$ und  $p$ bestimmen.

Diese vorgegebene Binomialverteilung soll hier durch eine Poissonverteilung  $Y$ approximiert werden, gekennzeichnet durch die Rate  $\lambda$:

• Wertebereich:

$$Y = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 2\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.1cm} ,\hspace{0.05cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm}\}\hspace{0.05cm},$$

• Wahrscheinlichkeiten:

$$P_Y (Y = \mu) = \frac{\lambda^{\mu}}{\mu !} \cdot {\rm e}^{\lambda} \hspace{0.05cm},$$

• Erwartungswerte:

$$m_Y = \sigma_Y^2 = \lambda\hspace{0.05cm}.$$

Um abschätzen zu können, ob die Wahrscheinlichkeitsfunktion $P_X(X)$ ausreichend gut durch $P_Y(Y)$ approximiert wird, kann man auf die so genannten Kullback–Leibler–Distanzen (KLD) zurückgreifen, teilweise in der Literatur auch relative Entropien genannt. Angepasst an das vorliegende Beispiel lauten diese:

$$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{I} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm},$$

$$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{\infty} P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$

Bei Verwendung des Logarithmus dualis (zur Basis 2) ist hierbei dem Zahlenwert die Pseudo–Einheit „bit” hinzuzufügen.

Beiliegende Ergebnistabelle

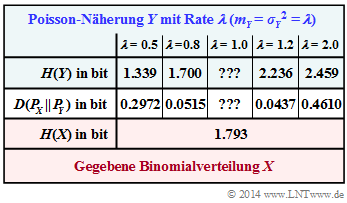
In nebenstehender Tabelle ist die Kullback–Leibler–Distanz $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ (in „bit”) zwischen Binomial–PMF $P_X(\cdot)$ und einigen Poisson–Näherungen $P_Y(\cdot)$ (mit fünf verschiedenen Raten $\lambda$) eingetragen. Die jeweilige Entropie  $H(Y)$, die ebenfalls von der Rate  $\lambda$ abhängt, ist in der ersten Zeile angegeben.

Die Spalten für $\lambda = 1$ sind in den Teilaufgaben (3) und (4) zu ergänzen. In der Teilaufgabe (6) sollen diese Ergebnisse interpretriert werden.
Hinweise:

• Die Aufgabe gehört zum Kapitel  Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
• Insbesondere wird Bezug genommen auf die Seite  Relative Entropie – Kullback-Leibler-Distanz.

• Um die numerischen Berechnungen in Grenzen zu halten, werden folgende Hilfsgrößen vorgegeben; hierbei bezeichnet $\rm \lg$ den Logarithmus zur Basis $10$:

$$A' = 0.4096 \cdot {\rm lg} \hspace{0.1cm} \frac{0.4096}{0.3679} + 0.2048 \cdot {\rm lg} \hspace{0.1cm} \frac{0.2048}{0.1839} + 0.0512 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0512}{0.0613} + 0.0064 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0064}{0.0153} + 0.0003 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0003}{0.0031} \hspace{0.05cm},$$

$$B' = 0.1839 \cdot {\rm lg} \hspace{0.1cm} (0.1839) + 0.0613 \cdot {\rm lg} \hspace{0.1cm} (0.0613) + 0.0153 \cdot {\rm lg} \hspace{0.1cm} (0.0153) + 0.0031 \cdot {\rm lg} \hspace{0.1cm} (0.0031) + 0.0005 \cdot {\rm lg} \hspace{0.1cm} (0.0005) + 0.0001 \cdot {\rm lg} \hspace{0.1cm} (0.0001)$$

$$\Rightarrow \hspace{0.3cm} A' \hspace{0.15cm} \underline {= 0.021944} \hspace{0.05cm},\hspace{0.5cm} B' \hspace{0.15cm} \underline {= -0.24717} \hspace{0.05cm}.$$

Fragebogen

1

Wie lauten die Kenngrößen der vorliegenden Binomialverteilung?
Hinweis: Geben Sie (maximal) eine Nachkommastelle ein.

$I \hspace{0.47cm} = \ $

$p \hspace{0.47cm} = \ $

$m_x \ = \ $

$\sigma^2_x \hspace{0.25cm} = \ $

2

Welche Kullback–Leibler–Distanz sollte man hier verwenden?

	Keine der beiden Distanzen ist anwendbar.
	$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ ist besser geeignet.
	$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X)$ ist besser geeignet.
	Beide Kullback–Leibler–Distanzen sind anwendbar.

3

Berechnen Sie die geeignete Kullback–Leibler–Distanz (hier mit $D$ abgekürzt) für  $\lambda = 1$.
Berücksichtigen Sie die Hilfsgröße  $A\hspace{0.05cm}'$.

$D \ = \ $ $\ \rm bit$

4

Berechnen Sie die Entropie  $H(Y)$ der Poisson–Näherung mit der Rate  $\lambda = 1$.
Berücksichtigen Sie die Hilfsgröße  $B\hspace{0.05cm}'$.

$H(Y) \ = \ $ $\ \rm bit$

5

Welche der folgenden Aussagen sind zutreffend?

	Bei der  $H(Y)$ –Berechnung haben alle Terme gleiches Vorzeichen.
	Bei der $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$–Berechnung haben alle Terme gleiches Vorzeichen.

6

Wie interpretieren Sie die vervollständigte Ergebnistabelle?

	Nach der Kullback–Leibler–Distanz sollte man  $\lambda = 1$ wählen.
	$\lambda = 1$ garantiert die beste Approximation  $H(Y) ≈ H(X)$.

Musterlösung

Musterlösung

(1)  Bei der Binomialverteilung sind alle Wahrscheinlichkeiten ${\rm Pr}(X > I) = 0$   ⇒   $\underline{I = 5}$.
Damit ergibt sich für die Wahrscheinlichkeit, dass $X =I = 5$ ist:

$${\rm Pr} (X = 5) = {5 \choose 5} \cdot p^{5} = p^{5} \approx 0.0003 \hspace{0.05cm}.$$

Somit erhält man für

• die charakteristische Wahrscheinlichkeit:   $p= (0.0003)^{1/5} = 0.1974 \hspace{0.15cm} \underline {\approx 0.2}\hspace{0.05cm},$
• den linearen Mittelwert (Erwartungswert):   $m_X = I \cdot p \hspace{0.15cm} \underline {= 1}\hspace{0.05cm},$
• die Varianz:   $\sigma_X^2 = I \cdot p \cdot (1-p) \hspace{0.15cm} \underline {= 0.8}\hspace{0.05cm}.$

(2)  Richtig ist der Lösungsvorschlag 2:

• Bei Verwendung von $D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X)$ würde sich unabhängig von $λ$ stets ein unendlicher Wert ergeben, da für $\mu ≥ 6$ gilt:

$$P_X (X = \mu) = 0 \hspace{0.05cm},\hspace{0.3cm}P_Y (Y = \mu) \ne 0 \hspace{0.05cm}.$$

• Auch wenn die Wahrscheinlichkeiten $P_Y (Y = \mu)$ für große $μ$ sehr klein werden, sind sie doch „unendlich viel größer” als $P_X (X = \mu)$.

(3)  Wir verwenden die erste Kullback–Leibler–Distanz:

$$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =\hspace{0.2cm} \sum_{\mu = 0}^{5} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm}.$$

Bei Verwendung des Zehnerlogarithmus $(\lg)$ erhalten wir für die Poisson–Näherung mit  $\lambda = 1$:

$$D \hspace{0.05cm}' = 0.3277 \cdot {\rm lg} \hspace{0.1cm} \frac{0.3277}{0.3679} + A \hspace{0.05cm}' = -0.016468 + 0.021944 = 0.005476 \hspace{0.05cm}.$$

Nach Umrechnung auf den Zweierlogarithmus $(\log_2)$ erhält man schließlich:

$$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{0.005476}{{\rm lg} \hspace{0.1cm}(2)} \hspace{0.15cm} \underline {\approx 0.0182\,{\rm (bit)}}\hspace{0.05cm}.$$

(4)  Unter Verwendung des Zehnerlogarithmus lautet die Entropie der Poisson–Näherung $(\lambda = 1)$:

$$H\hspace{0.05cm}'(Y) = -{\rm E} \left [{\rm lg} \hspace{0.1cm} {P_Y(Y)} \right ] = -2 \cdot 0.3679 \cdot {\rm lg} \hspace{0.1cm} (0.3679) - B\hspace{0.05cm}' = 0.31954 + 0.24717 = 0.56126.$$

Die Umrechnung in „bit” liefert das gesuchte Ergebnis:

$$H(Y) = \frac{0.56126}{{\rm lg} \hspace{0.1cm}(2)} \hspace{0.15cm} \underline {= 1.864\,{\rm (bit)}} \hspace{0.05cm}.$$

(5)  Richtig ist die Aussage 1. Bei der numerischen Berechnung der Kullback–Leibler–Distanz ist

• der Beitrag des $μ$–ten Terms positiv, falls $P_Y(\mu) > P_X(\mu)$,
• der Beitrag des $μ$–ten Terms negativ, falls $P_Y(\mu) < P_X(\mu)$.

Kullback–Leibler–Distanz und Entropie

(6)  Zutreffend ist der Lösungsvorschlag 1:

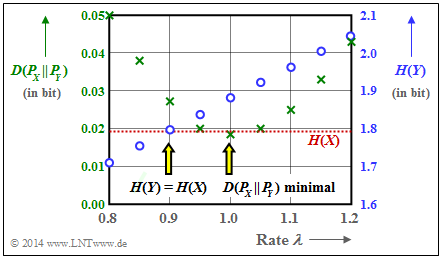
• Auch aus der Grafik ist ersichtlich, dass $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =0.0182$ bit von keinem anderen  $λ$–Wert als  $λ = 1$ unterschritten wird (grüne Kreuze).
• Weiter erkennt man aus dieser Darstellung, dass man mit  $λ = 0.9$ eine bessere Entropie–Approximation als mit  $λ = 1$ erreicht (blaue Kreise):

$$H(Y) = 1.795\,{\rm bit} \hspace{0.15cm}\approx \hspace{0.15cm} H(X) = 1.793\,{\rm bit}\hspace{0.05cm}.$$

Der zweite Lösungsvorschlag ist also falsch.

• Mit  $λ = 1$ stimmen die linearen Mittelwerte der beiden Zufallsgrößen überein:

$$m_X = m_Y= 1.$$

• Mit  $λ = 0.9$ stimmen die quadratischen Mittelwerte überein:

$$m_X + \sigma_X^2 = m_Y + \sigma_Y^2= 1.8.$$

Ob diese Aussage relevant ist, lasse ich dahingestellt. Denn:

Aufgrund der stetigen Zunahme von $H(Y)$ mit zunehmendem $λ$ ist klar, dass für irgendeinen $λ$–Wert tatsächlich $H(Y) = H(X)$ gelten muss.