Aufgabe 1.6Z: Rayleigh und Rice im Vergleich: Unterschied zwischen den Versionen
| Zeile 40: | Zeile 40: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie ergibt sich aus dem Rice–Modell ein idealer Kanal ⇒ H(f) = 1? |
|type="[]"} | |type="[]"} | ||
| − | + | + | - $x_0 = y_0 = 0, \sigma^2 = 1$. |
| − | - | + | + Mit $x_0 = 1, y_0 = 0, \sigma^2 = 0$. |
| + | - Mit $x_0 = 0, y_0 = 1, \sigma^2 = 0$. | ||
| − | { | + | {Ermitteln Sie aus der komplexen $z(t)$–Darstellung auf der Angabenseite die verwendeten Rice–Parameter. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma \ = \ $ { 0.316 3% } |
| + | $x_0 \ = \ $ { 0.632 3% } | ||
| + | $y_0 \ = \ $ { 0.632 3% } | ||
| + | |||
| + | {Bei welchem Kanal wird ${\rm Pr}(20 \cdot {\rm lg} \, |z(t)| ≤ \ –6 \ \rm dB)$ größer sein? | ||
| + | |type="[]"} | ||
| + | + Beim vorliegenden Rayleigh–Kanal. | ||
| + | - Beim vorliegenden Rice–Kanal. | ||
| + | - Die Wahrscheinlichkeiten sind näherungsweise gleich. | ||
| + | |||
| + | {Bei welchem Kanal wird ${\rm Pr}(20 \cdot {\rm lg} \, |z(t)| ≤ 0 \ \rm dB)$ größer sein? | ||
| + | |type="[]"} | ||
| + | - ${\rm Pr}(20 \cdot {\rm lg} \, |z(t)| ≤ 0 \ \rm dB)$ ist beim Rice–Kanal deutlich kleiner. | ||
| + | - ${\rm Pr}(20 \cdot {\rm lg} \, |z(t)| ≤ 0 \ \rm dB)$ ist beim Rice–Kanal deutlich größer. | ||
| + | + Die Wahrscheinlichkeiten sind näherungsweise gleich. | ||
| + | |||
| + | {Welche Aussagen treffen für ein BPSK–Sendesignal $s(t)$ zu, wenn man die komplexe Darstellung des Empfängersignals $r(t)$ betrachtet? | ||
| + | |type="[]"} | ||
| + | - Rayleigh–Fading bewirkt Punktwolken in Quadrant 1 und 3. | ||
| + | + Rice–Fading bewirkt Punktwolken in Quadrant 1 und 3. | ||
| + | + Bei Rayleigh ist die WDF von $|r(t)|$ gleich der WDF von $|z(t)|$. | ||
| + | - Bei Rice ist die WDF von $|r(t)|$ gleich der WDF von $|z(t)|$. | ||
</quiz> | </quiz> | ||
Version vom 16. November 2017, 23:59 Uhr
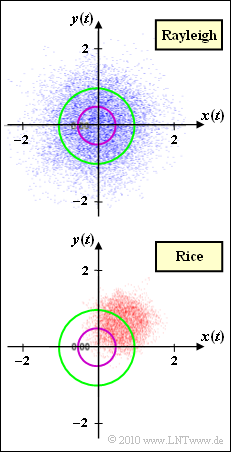
In dieser Aufgabe sollen Rayleigh–Fading und Rice–Fading miteinander verglichen werden.
Die Grafik zeigt den komplexen Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ in der komplexen Ebene. Für das TP–Sendesignal $s(t) = 1$, was bezüglich eines BP–Systems einer Cosinusschwingung mit der Amplitude $1$ entspricht, ist das TP–Empfangssignal $r(t)$ identisch mit $z(t)$.
Das obere Diagramm beschreibt Rayleigh–Fading, wobei die Komponentensignale $x(t)$ und $y(t)$ jeweils gaußverteilt sind mit Varianz $\sigma^2$. Die Wahrscheinlichkeitsdichtefunktion des Betrags $a(t) = |z(t)|$ lautet für $a ≥ 0$:
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 }{2\sigma^2}] \hspace{0.05cm}.$$
Der quadratische Erwartungswert von $z(t)$ ist $1$:
- $${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma = {1}/{\sqrt{2}} \approx 0.707 \hspace{0.05cm}.$$
Das untere Phasendiagramm entsteht bei Rice–Fading. Auch hier sind $x(t)$ und $y(t)$ gaußverteilt mit Varianz $\sigma^2$, aber nun mit Mittelwert $x_0$ bzw. $y_0$.
Die WDF lautet mit der modifizierten Besselfunktion ${\rm I}_0$ für $a ≥ 0$:
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}.$$
Der quadratische Mittelwert beinhaltet nun auch die Direktkomponente $z_0 = x_0 + {\rm j} \cdot y_0$:
- $${\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$
Für den Systemvergleich
- wird von konstantem ${\rm E}[|z(t)|^2] = 1$ ausgegangen,
- wird beim Rice–Fading von der aus der Grafik erkennbaren Vorzugsrichtung ausgegangen,
- sei die Leistung zwischen Direktpfad ($|z_0|^2$) Streupfaden ($2\sigma^2$) im Verhältnis $4:1$ aufgeteilt.
Für die Teilaufgaben (1) bis (4) gelte $s(t) = 1$, während in den Teilaufgaben (5) bzw. (6) ein BPSK–Signal vorausgesetzt wird. Das TP–Signal $s(t)$ hat somit einen rechteckförmigen Verlauf mit den möglichen Werten $±1$. Die Dauer eines Rechteckimpulses sei $T = 10 \ \rm ms$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Nichtfrequenzselektives Fading mit Direktkomponente.
- Die in der Grafik eingezeichneten Kreise (violett und grün) beziehen sich auf die Teilaufgaben (3) und (4).
Fragebogen
Musterlösung