Applets:Kohärentes und inkohärentes On-Off-Keying: Unterschied zwischen den Versionen
Höfler (Diskussion | Beiträge) |
|||
| (42 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{ | + | {{LntAppletLinkDeEn|on-off-keying|on-off-keying_en}} |
| − | + | ||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
<br> | <br> | ||
| − | + | Betrachtet wird die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ von On–Off–Keying bei weißem Rauschen, gekennzeichnet durch die Streuung $\sigma_{\rm AWGN}$, und zwar sowohl bei kohärenter Demodulation als auch bei inkohärenter Demodulation. Dargestellt werden für beide Fälle die Wahrscheinlichkeitsdichtefunktionen des Empfangssignals für die möglichen Sendesymbole $s_0$ und $s_1 \equiv 0$. | |
| − | + | *Im kohärenten Fall ergeben sich zwei Gaußfunktionen um $s_0$ und $s_1$. | |
| − | + | *Im inkohärenten Fall gibt es eine Rayleigh–WDF für das Symbol $s_1 = 0$ und eine Rice–WDF für $s_0 \ne 0$, deren Form auch vom Eingabeparameter $C_{\rm Rice}$ abhängt. | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Als Zahlenwerte ausgegeben werden die Verbundwahrscheinlichkeiten ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1})$ ⇒ (ausgefüllte blaue Fläche in der WDF–Grafik) und ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0})$ ⇒ (rote Fläche) sowie als Endergebnis $p_{\rm S} = {\rm Pr}(\boldsymbol{r} \ne \boldsymbol{s})= {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$ | ||
| + | *Alle diese Größen hängen auch von der Entscheiderschwelle $G$ ab, dessen jeweils optimaler Wert ebenfalls ermittelt wird. | ||
| + | *Außerdem zeigt das Applet, welchen Fehler man macht, wenn man die im allgemeinen kompliziertere Rice–WDF durch die bestmögliche Gauß–WDF approximiert. | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| Zeile 26: | Zeile 21: | ||
[[Datei:P ID2054 Dig T 4 4 S3 version1.png|right|frame|Signalraumkonstellationen für On–Off–Keying|class=fit]] | [[Datei:P ID2054 Dig T 4 4 S3 version1.png|right|frame|Signalraumkonstellationen für On–Off–Keying|class=fit]] | ||
| − | $\rm OOK$ ist ein eindimensionales Modulationsverfahren mit | + | $\rm OOK$ ist ein binäres und eindimensionales Modulationsverfahren, zum Beispiel mit $s_{1} \equiv 0$ und |
| − | + | *$\boldsymbol{s}_{0} = \{s_0,\ 0\}$ (bei Cosinus–Träger, linke Grafik) bzw. | |
| − | *$ | + | *$\boldsymbol{s}_{0} = \{0,\ -s_0\}$ (bei Sinus–Träger, rechte Grafik). |
| − | |||
| − | + | Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht wieder aus den zwei Punkten $\boldsymbol{r}_0=\boldsymbol{s}_0$ und $\boldsymbol{r}_1=\boldsymbol{s}_1$. In diesem Fall ist das AWGN–Rauschen eindimensional mit der Varianz $\sigma_{\rm AWGN}^2$ anzusetzen und man erhält entsprechend dem [[Digitalsignalübertragung/Approximation_der_Fehlerwahrscheinlichkeit#Fehlerwahrscheinlichkeit_bei_gleichwahrscheinlichen_Symbolen| Theorieteil]] für die '''Symbolfehlerwahrscheinlichkeit''' $p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s})$: | |
| − | + | :$$p_{\rm S} = {\rm Q} \left ( \frac{s_0/2}{\sigma_{\rm AWGN}}\right ) | |
| − | = | + | = {\rm Q} \left ( \sqrt{ {E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}. $$ |
| − | + | Hierzu ist anzumerken: | |
| − | |||
*Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Komplementäre Gaußsche Fehlerfunktionen]]. | *Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Komplementäre Gaußsche Fehlerfunktionen]]. | ||
| + | *Obige Gleichung gilt für gleichwahrscheinliche Symbole mit der Entscheiderschwelle $G$ in der Mitte zwischen $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.<br> | ||
| + | *Der Abstand der beiden Signalpunkte von der Entscheiderschwelle $G$ beträgt somit jeweils $\Delta G = s_0/2$ $($Zähler im Argument der ersten $\rm Q$–Funktion$)$. | ||
| + | *$E_{\rm S}=s_0^2/2 \cdot T$ bezeichnet für diesen Fall die „mittlere Energie pro Symbol” und $N_0=2T \cdot \sigma_{\rm AWGN}^2$ die (einseitige) AWGN–Rauschleistungsdichte. | ||
| − | |||
| − | + | [[Datei:Applet_Bild3.png|right|frame| $p_{\rm S}$–Berechnung für kohärente Demodulation]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Es gelte $\sigma_{\rm AWGN}= 0.8$ und $s_{0} = 2$, ⇒ $G=1$. Alle diese Werte seien auf den Wert $1\hspace{0.05cm} {\rm V}$ normiert. | ||
| − | + | Die Grafik zeigt zwei „halbe Gaußfunktionen” um $s_1=0$ (blaue Kurve) und $s_0=2$ (rote Kurve) sowie den Schwellenwert $G$. Die schraffierten Flächen markieren die Symbolfehlerwahrscheinlichkeit. | |
| − | + | *Nach der ersten Gleichung gilt mit $\Delta G = s_{0} -G= G-s_1 = 1$: | |
| − | + | :$$p_{\rm S} = {\rm Q} ( 1/0.8 )= {\rm Q} ( 1.25 )\approx 10.56 \%.$$ | |
| − | + | *Ebenso liefert die zweite Gleichung: $E_{\rm S}/{N_0} = 1/4 \cdot s_0^2/\sigma_{\rm AWGN}^2 = 1.5615$: | |
| + | :$$p_{\rm S} = {\rm Q} (\sqrt{1.5615} )\approx 10.56 \%.$$ | ||
| − | |||
| − | + | Aufgrund der Symmetrie ist der Schwellenwert $G=1$ optimal. In diesem Fall sind die rote und die blaue schraffierte Fläche gleich groß ⇒ die Symbole $\boldsymbol{s}_{0}$ und $\boldsymbol{s}_{1}$ werden in gleicher Weise verfälscht. | |
| − | :: | + | Mit $G\ne 1$ ergibt sich eine größere Verfälschungswahrscheinlichkeit. Beispielsweise ergibt sich mit $G=0.6$: |
| − | + | :$$p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) | |
| − | + | + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0})= 1/2 \cdot {\rm Q} ( 0.75)+ 1/2 \cdot {\rm Q} ( 1.75)\approx 13.33\% .$$ | |
| + | Hier ist die Verfälschungswahrscheinlichkeit für das Symbol $\boldsymbol{s}_{1}$ ⇒ blaue gefüllte Fläche ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 11.33\%$ aufgrund der ungünstig gewählten Entscheiderschwelle sehr viel größer als die des Symbols $\boldsymbol{s}_{0}$ ⇒ rote gefüllte Fläche ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 2\%$. }} | ||
| + | ===On–Off–Keying mit inkohärenter Demodulation=== | ||
| + | Die folgende Grafik zeigt die Strukur (im äquivalenten Tiefpassbereich) des optimalen OOK–Empfängers für inkohärente Demodulation. [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_On.E2.80.93Off.E2.80.93Keying|Detailbeschreibung]] | ||
| − | + | [[Datei:P ID3147 Dig T 4 5 S2b version1.png|right|frame|Empfänger für inkohärente OOK-Demodulation (komplexe Signale sind blau beschriftet)|class=fit]] | |
| − | : | + | Entsprechend dieser zweiten Grafik gilt: |
| − | + | *Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ am Empfänger ist aufgrund des aktuellen Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex. | |
| + | *Erforderlich ist nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer [[Digitalsignalübertragung/Signale,_Basisfunktionen_und_Vektorräume#Basisfunktionen_komplexer_Zeitsignale| komplexen Basisfunktion]] $\boldsymbol{\xi}(t)$.<br> | ||
| − | + | *Das Ergebnis ist der (komplexe) Detektorwert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.<br> | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| + | *Ist $y \gt G$, so wird als Schätzwert $m_0$ für das Symbol $\boldsymbol{s}_{0}$ ausgegeben, andernfalls der Schätzwert $m_1$ für das Symbol $\boldsymbol{s}_{1}$. | ||
| + | *Auch hier ist die mittlere Symbolfehlerwahrscheinlichkeit als Summe zweier Verbundwahrscheinlichkeiten darstellbar: | ||
| − | + | :$$p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) | |
| + | + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$$ | ||
| − | |||
| − | |||
| − | + | ===Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Rayleigh– und Riceverteilung=== | |
| − | + | Zur Berechnung der Symbolfehlerwahrscheinlichkeit bei inkohärenter Demodulation gehen wir von folgender Grafik aus. Dargestellt ist das Empfangssignal im äquivalenten Tiefpassbereich in der komplexen Ebene. | |
| − | [[Datei: | + | [[Datei:Applet_Bild1.png|right|frame|Zur Fehlerwahrscheinlichkeitsberechnung bei inkohärenter Demodulation|class=fit]] |
| − | + | *Der Punkt $\boldsymbol{s_1}=0$ führt im Empfangsignal wieder zu $\boldsymbol{r_1}=0$. | |
| − | * | + | *Dagegen kann $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ auf jedem Punkt eines Kreises mit Radius $1$ liegen, da die Phase $\phi$ unbekannt ist.<br> |
| − | * | + | *Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun zweidimensional zu interpretieren, wie durch die Pfeile in der Grafik angedeutet.<br> |
| + | |||
| + | *Die Entscheidungsregion $I_1$ für das Symbol $\boldsymbol{s_1}$ ist der blau gefüllte Kreis mit Radius $G$, wobei der richtige Wert von $G$ noch zu bestimmen ist. | ||
| − | * | + | *Liegt der Empfangswert $\boldsymbol{r}$ außerhalb dieses Kreises also im rot hinterlegten Gebiet $I_0$, so fällt die Entscheidung zugunsten von $\boldsymbol{s_0}$.<br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | $\rm Rayleigh–Anteil$<br> | |
| − | + | Unter Berücksichtigung des AWGN–Rauschens gilt $\boldsymbol{r_1}=\boldsymbol{s_1} + \boldsymbol{n_1}$. Die Rauschkomponente $\boldsymbol{n_1}$ besitzt eine [[Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung|Rayleighverteilung]] $($Betrag der beiden mittelwertfreien Gaußkomponenten für $I$ und $Q)$. | |
| − | $\ | ||
| − | |||
| − | |||
| + | Deren bedingte WDF lautet mit der rotationssymmetrischen Rauschkomponente $\eta$ mit $\sigma=\sigma_{\rm AWGN}$ : | ||
| + | :$$f_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1})=\frac{\eta}{\sigma^2}\cdot {\rm e}^{-\eta^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma^2) } = f_{\rm Rayleigh}(\eta) .$$ | ||
| + | Damit erhält man für die bedingte Wahrscheinlichkeit | ||
| + | :$${\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1}) = \int_{G}^{\infty}f_{\rm Rayleigh}(\eta) \,{\rm d} \eta | ||
| + | \hspace{0.05cm},$$ | ||
| + | und mit dem Faktor $1/2$ wegen der gleichwahrscheinlichen Sendesymbole die Verbundwahrscheinlichkeit: | ||
| + | :$${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) = 1/2 \cdot {\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1})= 1/2 \cdot \int_{G}^{\infty}f_{\rm Rayleigh}(\eta) \,{\rm d} \eta | ||
| + | \hspace{0.05cm}.$$ | ||
| − | Die | + | $\rm Rice–Anteil$<br> |
| − | = | + | Die Rauschkomponente $\boldsymbol{n_0}$ besitzt eine [[Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung|Riceverteilung]] $($Betrag der Gaußkomponenten mit Mittelwerten $m_x$ und $m_y)$ ⇒ Konstante $C=\sqrt{m_x^2 + m_y^2}$<br>$($''Anmerkung'': Im Applet wird die Konstante $C$ mit $C_{\rm Rice}$ bezeichnet$)$. |
| − | + | ||
| − | :$$ | + | :$$f_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) = f_{\rm Rice}(\eta) \hspace{1.4cm}{\rm mit} \hspace{1.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$ |
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | {\rm | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Damit ergibt sich für die zweite Verbundwahrscheinlichkeit: | ||
| + | |||
| + | :$${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) = 1/2 \cdot \int_{0}^{G}f_{\rm Rice}(\eta) \,{\rm d} \eta | ||
| + | \hspace{0.05cm}.$$ | ||
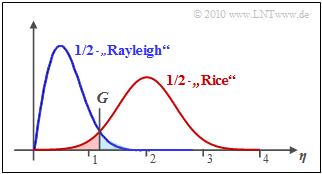
| + | [[Datei:Applet_Bild2.png|right|frame|Dichtefunktionen für „OOK, inkohärent”]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel:}$ | + | $\text{Beispiel 2:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_{\rm AWGN} = 0.5$ und $C_{\rm Rice} = 2$. Die Entscheidungsgrenze liegt bei $G \approx 1.25$. Man erkennt aus dieser Darstellung: |
| − | + | *Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. Wie im Beispiel 1 für den kohärenten Fall gilt auch hier: | |
| − | + | :$$p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) | |
| − | + | + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$$ | |
| − | + | *Die blau markierte Fläche gibt die Verbundwahrscheinlichkeit ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 2.2\%$ an. Diese berechnet sich als das Integral über die halbe Rayleigh–WDF im Bereich von $G$ bis $\infty$. | |
| − | + | *Die rot markierte Fläche gibt die Verbundwahrscheinlichkeit ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 2.4\%$ an. Diese berechnet sich als das Integral über die halbe Rice–WDF im Bereich von $0$ bis $G$. | |
| − | + | *Somit erhält man $p_{\rm S} \approx 4.6\%$. Anzumerken ist, dass die roten und blauen Flächen nicht gleich sind und dass sich die optimale Entscheidungsgrenze $G_{\rm opt}$ sich aus dem Schnittpunkt der beiden Kurven ergibt. | |
| − | + | *Die optimale Entscheidungsgrenze $G_{\rm opt}$ ergibt sich als der Schnittpunkt von blauer und roter Kurve.}} | |
| − | *Die | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | :$$ | ||
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | *Die | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Versuchsdurchführung== | ==Versuchsdurchführung== | ||
<br> | <br> | ||
| − | |||
| − | *Wählen Sie | + | *Wählen Sie die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe. Die Nummer „$0$” entspricht einem „Reset”: Einstellung wie beim Programmstart. |
| − | + | *Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”. | |
| − | + | *Interpretieren Sie stets die Grafiken und die numerischen Ergebnisse. Die Symbole $s_0$ (einstellbar) und ${s}_{1}\equiv 0$ seien gleichwahrscheinlich. | |
| − | + | *Aus Platzgründen verwenden wir bei den folgenden Fragen und Musterlösungen teilweise auch $\sigma = \sigma_{\rm AWGN}$ und $C = C_{\rm Rice}$.<br> | |
| − | *„ | ||
| − | * | ||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' | + | '''(1)''' Wir betrachten die '''kohärente Demodulation''' mit $\sigma_{\rm AWGN} = 0.5$ und $s_0 = 2$. Was ist der kleinstmögliche Wert für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$? }} |
| − | |||
| − | * | + | *Bei kohärenter Demodulation setzt sich die WDF des Empfangssignals aus zwei „halben” Gaußfunktionen um $s_0 = 2$ $($rot$)$ und $s_1 = 0$ $($blau$)$ zusammen. |
| − | + | *Der minimale $p_{\rm S}$–Wert ergibt sich hier mit $G=1$ sowie $\Delta G = s_{0} -G= G-s_1 = 1$ zu $p_{\rm S}= {\rm Q} ( \Delta G/\sigma )={\rm Q} ( 1/0.5 )= {\rm Q} ( 2 )\approx 2.28 \%.$ | |
| − | + | *Mit $G=1$ werden beide Symbole gleich verfälscht. Die blaue Fläche ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1})$ ist gleich der roten Fläche ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0})$. Deren Summe ergibt $p_{\rm S}$. | |
| − | * | + | *Mit $G=0.5$ ist zwar die rote Fläche nahezu Null. Trotzdem ist $p_{\rm S}\approx 8\%$ (Summe beider Flächen) mehr als doppelt so groß als mit $G_{\rm opt}=1$. |
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | '''(2)''' | + | '''(2)''' Nun gelte $\sigma = 0.75$. Mit welchem $s_0$–Wert ergibt sich bei optimalem $G$ die gleiche Fehlerwahrscheinlichkeit wie in $(1)$? Wie groß ist dann der Quotient $E_{\rm S}/N_0$?}} |
| − | * | + | *Allgemein gilt $p_{\rm S}= {\rm Q}\big ( (s_0/2) / \sigma \big )$. Erhöht man $\sigma$ von $0.5$ auf $0.75$, dann muss auch $s_0$ erhöht werden ⇒ $s_0 = 3$ ⇒ $p_{\rm S}= {\rm Q} ( 1.5/ 0.75 )= {\rm Q} ( 2 )$. |
| − | * | + | *Außer $p_{\rm S}= {\rm Q}\big ( (s_0/2) / \sigma \big )$ gilt aber auch: $p_{\rm S}= {\rm Q} ( \sqrt{E_{\rm S}/N_0} )$. Daraus folgt: $p_{\rm S}= {\rm Q}(2) ={\rm Q} ( \sqrt{E_{\rm S}/N_0})$ ⇒ $\sqrt{E_{\rm S}/N_0}= 2$ ⇒ $E_{\rm S}/N_0= 4$. |
| + | *Zur Kontrolle: $E_{\rm S}=s_0^2/2 \cdot T, \ N_0=2T \cdot \sigma^2$ ⇒ $E_{\rm S}/N_0 =s_0^2/(4 \cdot \sigma^2)= 3^2/(4 \cdot 0.75^2)=4$. Das gleiche $E_{\rm S}/N_0 =4$ ergibt sich für die Aufgabe '''(1)'''. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' | + | '''(3)''' Nun betrachten wir die '''inkohärente Demodulation''' mit $\sigma_{\rm AWGN} = 0.75$, $C_{\rm Rice} = 2.25$ und $G=2$. Wie groß ist die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$? }} |
| − | * | + | *Bei inkohärenter Demodulation setzt sich die WDF des Empfangssignals aus einer „halben” Rayleighfunktion $($blau$)$ und einer „halben” Ricefunktion $($rot$)$ zusammen. |
| − | * | + | *${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 1.43\%$ gibt die Anteile der blauen Kurve oberhalb von $G =2$ an, und ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 15.18\%$ die Anteile der roten Kurve unterhalb von $G =2$. |
| − | + | *Mit $G=2$ ergibt sich für die Symbolfehlerwahrscheinlichkeit die Summe $p_{\rm S}\approx 16.61\%$ , und mit $G_{\rm opt}=1.58$ ein geringfügig besserer Wert: $p_{\rm S}\approx 12.25\%$. | |
| − | * | ||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' | + | '''(4)''' Es sei $X$ allgemein eine Rayleigh–Zufallsgröße und $Y$ eine Rice–Zufallsgröße, jeweils mit obigen Parametern. Wie groß sind ${\rm Pr}(X\le 2)$ und ${\rm Pr}(Y\le 2)$ ?}} |
| − | * | + | * Es gilt ${\rm Pr}(Y\le 2) = 2 \cdot {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 30.36\%$, da im Programm die Rice–WDF mit dem Faktor $1/2$ dargestellt ist. |
| − | + | *In gleicher Weise gilt ${\rm Pr}(X> 2) = 2 \cdot {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 2.86\%$ ⇒ ${\rm Pr}(X \le 2)= 1-0.0286 = 97.14\%$. | |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(5)''' | + | '''(5)''' Wir betrachten die Werte $\sigma_{\rm AWGN} = 0.75$, $C_{\rm Rice} = 2.25$ und $G=G_{\rm opt}=1.58$. Wie ändert sich $p_{\rm S}$, wenn man „Rice” bestmöglich durch „Gauß” ersetzt? }} |
| − | * | + | *Nach der exakten Berechnung ergibt sich mit der optimalen Schwelle $G_{\rm opt}=1.58$: ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 5.44\%$, ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 6.81\%$ ⇒ $p_{\rm S}\approx 12.25\%$. |
| − | * | + | *Mit der Gaußnäherung wird bei gleichem $G$ der erste Term nicht verändert. Der zweite Term erhöht sich auf ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 9.29\%$ ⇒ $p_{\rm S}\approx 14.73\%$. |
| − | * | + | *Die neue Optimierung des Schwellenwerts $G$ unter Berücksichtigung der Gaußnäherung führt auf $G_{\rm opt}=1.53$ und $p_{\rm S}\approx 14.67\%$. |
| + | *Die Parameter der Gaußverteilung sind dabei wie folgt einzustellen: Mittelwert $m_{\rm Gauß}= C_{\rm Rice}=2.25$, Streuung $\sigma_{\rm Gauß}= \sigma_{\rm AWGN}=0.75$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' | + | '''(6)''' Wie ändern sich die Ergebnisse gegenüber $(5)$ mit $\sigma_{\rm AWGN} = 0.5$, $C_{\rm Rice} = 1.5$ bzw. mit $\sigma_{\rm AWGN} = 1$, $C_{\rm Rice} = 3$, jeweils mit $G=G_{\rm opt}$? }} |
| − | + | ||
| − | *Bei | + | *Bei optimaler Entscheidungsgrenze ergeben sich stets gleiche Wahrscheinlichkeiten, sowohl für die exakte Riceverteilung als auch mit der Gaußnäherung. |
| − | *Bei | + | *Bei allen drei Parametersätzen gilt $E_{\rm S}/N_0= 2.25$. Dies lässt vermuten: die Ergebnisse bei inkohärenter Demodulation hängen allein von dieser Kenngröße ab. |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(7)''' | + | '''(7)''' Die Einstellung sei weiterhin „inkohärent mit Näherung”. Es gelte stets $C_{\rm Rice} = 3$, $G=G_{\rm opt}$. Variierern Sie die AWGN–Streuung im Bereich $0.5 \le \sigma \le 1$.<br> Interpretieren Sie den relativen Fehler „Falsch minus Richtig/Richtig” in Abhängigkeit der Kenngröße $E_{\rm S}/N_0$.}} |
| − | * | + | *Mit $\sigma =0.5$ ⇒ $E_{\rm S}/N_0 = 9$ erhält man $p_{\rm S}^{\ \rm exakt}\approx 0.32\%$ und $p_{\rm S}^{\ \rm Näherung}\approx 0.38\%$. Der absolute Fehler beträgt $0.06\%$ und der relative Fehler $18.75\%$. |
| − | + | *Mit $\sigma =1$ ⇒ $E_{\rm S}/N_0 = 2.25$ erhält man $p_{\rm S}^{\ \rm exakt}\approx 12.25\%$ und $p_{\rm S}^{\ \rm Näherung}\approx 14.67\%$. Der absolute Fehler beträgt $2.42\%$ und der relative Fehler $19.75\%$. | |
| + | * '''Fazit''': Die Gaußnäherung wird mit größerem $E_{\rm S}/N_0$ immer besser. Diese Aussage erkennt man am absoluten Fehler deutlicher als am relativen Fehler. | ||
| − | == | + | {{BlaueBox|TEXT= |
| + | '''(8)''' Wiederholen Sie den letzten Versuch nun mit der Einstellung „kohärent” sowie $s_0 = 3$, $G=G_{\rm opt}$. Welches Fazit erlaubt der Vergleich mit '''(7)'''? }} | ||
| + | |||
| + | *Der Vergleich von $(7)$ und $(8)$ zeigt: Für jedes $E_{\rm S}/N_0$ ergibt sich bei inkohärenter Demodulation eine größere Symbolfehlerwahrscheinlichkeit. | ||
| + | *Für $E_{\rm S}/N_0= 9$ ergibt sich $p_{\rm S}^{\ \rm kohärent}\approx 0.13\%$ und $p_{\rm S}^{\ \rm inkohärent}\approx 0.32\%$. Und für $E_{\rm S}/N_0= 2.25$ erhält man $p_{\rm S}^{\ \rm kohärent}\approx 6.68\%$ und $p_{\rm S}^{\ \rm inkohärent}\approx 12.25\%$. | ||
| + | *Die einfachere Realisierung des inkohärenten Demodulators (keine Taktsynchronisierung) bewirkt einen Qualitätsverlust ⇒ größere Fehlerwahrscheinlichkeit. | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Zur Handhabung des Applets== | |
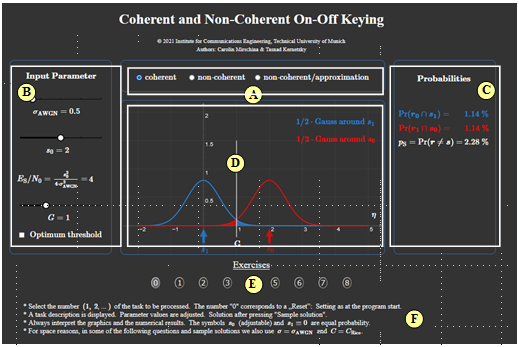
| + | [[Datei:Exercise_OnOff.png |right|frame|Bildschirmabzug der englischen Version ]] | ||
| − | '''( | + | '''(A)''' Auswahl: |
| + | ::*Kohärent, | ||
| + | ::*inkohärent, | ||
| + | ::*inkohärent mit Näherung. | ||
| − | '''( | + | '''(B)''' Parametereingabe: |
| + | ::*$\sigma_{\rm AWGN}$, | ||
| + | ::*$s_0$, | ||
| + | ::*$E_{\rm S}/N_0$, | ||
| + | ::*$G_{\rm opt}$ | ||
| − | '''( | + | '''(C)''' Numerischer Ausgabebereich der Wahrscheinlichkeiten |
| − | '''( | + | '''(D)''' Grafischer Ausgabebereich der WDF-Anteile |
| − | '''( | + | '''(E)''' Aufgabenauswahl |
| − | '''( | + | '''(F)''' Fragen und Lösungen |
| − | + | <br clear = all> | |
| − | + | ==Über die Autoren== | |
| − | + | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | |
| − | + | *Die erste Version wurde 2011 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Martin_V.C3.B6lkl_.28Diplomarbeit_LB_2010.29|Martin Völkl]] im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]] und [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Dr.-Ing._Klaus_Eichin_.28am_LNT_von_1972-2011.29|Klaus Eichin]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | + | *2020 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] im Rahmen einer Werkstudententätigkeit auf „HTML5/JS” umgesetzt und neu gestaltet (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29|Tasnád Kernetzky]]). | |
| − | + | *Diese Umsetzung wurde von der Fakultät Elektrotechnik & Informationstechnik der TU München durch [https://www.ei.tum.de/studium/studienzuschuesse/ "Studienzuschüsse"] finanziell unterstützt. Wir bedanken uns. | |
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | + | {{LntAppletLinkDeEn|on-off-keying|on-off-keying_en}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br><br> | <br><br> | ||
Aktuelle Version vom 26. Oktober 2023, 11:59 Uhr
Applet in neuem Tab öffnen Open English Version
Inhaltsverzeichnis
Programmbeschreibung
Betrachtet wird die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ von On–Off–Keying bei weißem Rauschen, gekennzeichnet durch die Streuung $\sigma_{\rm AWGN}$, und zwar sowohl bei kohärenter Demodulation als auch bei inkohärenter Demodulation. Dargestellt werden für beide Fälle die Wahrscheinlichkeitsdichtefunktionen des Empfangssignals für die möglichen Sendesymbole $s_0$ und $s_1 \equiv 0$.
- Im kohärenten Fall ergeben sich zwei Gaußfunktionen um $s_0$ und $s_1$.
- Im inkohärenten Fall gibt es eine Rayleigh–WDF für das Symbol $s_1 = 0$ und eine Rice–WDF für $s_0 \ne 0$, deren Form auch vom Eingabeparameter $C_{\rm Rice}$ abhängt.
Als Zahlenwerte ausgegeben werden die Verbundwahrscheinlichkeiten ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1})$ ⇒ (ausgefüllte blaue Fläche in der WDF–Grafik) und ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0})$ ⇒ (rote Fläche) sowie als Endergebnis $p_{\rm S} = {\rm Pr}(\boldsymbol{r} \ne \boldsymbol{s})= {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$
- Alle diese Größen hängen auch von der Entscheiderschwelle $G$ ab, dessen jeweils optimaler Wert ebenfalls ermittelt wird.
- Außerdem zeigt das Applet, welchen Fehler man macht, wenn man die im allgemeinen kompliziertere Rice–WDF durch die bestmögliche Gauß–WDF approximiert.
Theoretischer Hintergrund
On–Off–Keying mit kohärenter Demodulation
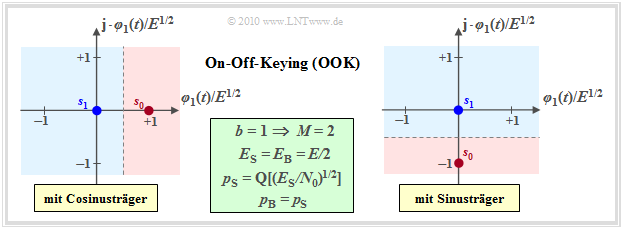
Das einfachste digitale Modulationsverfahren ist On–Off–Keying $\rm (OOK)$. Dieses Verfahren wird teilweise auch als Amplitude Shift Keying $\rm (2–ASK)$ bezeichnet und kann im äquivalenten Tiefpassbereich wie folgt charakterisiert werden:
$\rm OOK$ ist ein binäres und eindimensionales Modulationsverfahren, zum Beispiel mit $s_{1} \equiv 0$ und
- $\boldsymbol{s}_{0} = \{s_0,\ 0\}$ (bei Cosinus–Träger, linke Grafik) bzw.
- $\boldsymbol{s}_{0} = \{0,\ -s_0\}$ (bei Sinus–Träger, rechte Grafik).
Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht wieder aus den zwei Punkten $\boldsymbol{r}_0=\boldsymbol{s}_0$ und $\boldsymbol{r}_1=\boldsymbol{s}_1$. In diesem Fall ist das AWGN–Rauschen eindimensional mit der Varianz $\sigma_{\rm AWGN}^2$ anzusetzen und man erhält entsprechend dem Theorieteil für die Symbolfehlerwahrscheinlichkeit $p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s})$:
- $$p_{\rm S} = {\rm Q} \left ( \frac{s_0/2}{\sigma_{\rm AWGN}}\right ) = {\rm Q} \left ( \sqrt{ {E_{\rm S}}/{N_0}}\right ) \hspace{0.05cm}. $$
Hierzu ist anzumerken:
- Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet Komplementäre Gaußsche Fehlerfunktionen.
- Obige Gleichung gilt für gleichwahrscheinliche Symbole mit der Entscheiderschwelle $G$ in der Mitte zwischen $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.
- Der Abstand der beiden Signalpunkte von der Entscheiderschwelle $G$ beträgt somit jeweils $\Delta G = s_0/2$ $($Zähler im Argument der ersten $\rm Q$–Funktion$)$.
- $E_{\rm S}=s_0^2/2 \cdot T$ bezeichnet für diesen Fall die „mittlere Energie pro Symbol” und $N_0=2T \cdot \sigma_{\rm AWGN}^2$ die (einseitige) AWGN–Rauschleistungsdichte.
$\text{Beispiel 1:}$ Es gelte $\sigma_{\rm AWGN}= 0.8$ und $s_{0} = 2$, ⇒ $G=1$. Alle diese Werte seien auf den Wert $1\hspace{0.05cm} {\rm V}$ normiert.
Die Grafik zeigt zwei „halbe Gaußfunktionen” um $s_1=0$ (blaue Kurve) und $s_0=2$ (rote Kurve) sowie den Schwellenwert $G$. Die schraffierten Flächen markieren die Symbolfehlerwahrscheinlichkeit.
- Nach der ersten Gleichung gilt mit $\Delta G = s_{0} -G= G-s_1 = 1$:
- $$p_{\rm S} = {\rm Q} ( 1/0.8 )= {\rm Q} ( 1.25 )\approx 10.56 \%.$$
- Ebenso liefert die zweite Gleichung: $E_{\rm S}/{N_0} = 1/4 \cdot s_0^2/\sigma_{\rm AWGN}^2 = 1.5615$:
- $$p_{\rm S} = {\rm Q} (\sqrt{1.5615} )\approx 10.56 \%.$$
Aufgrund der Symmetrie ist der Schwellenwert $G=1$ optimal. In diesem Fall sind die rote und die blaue schraffierte Fläche gleich groß ⇒ die Symbole $\boldsymbol{s}_{0}$ und $\boldsymbol{s}_{1}$ werden in gleicher Weise verfälscht.
Mit $G\ne 1$ ergibt sich eine größere Verfälschungswahrscheinlichkeit. Beispielsweise ergibt sich mit $G=0.6$:
- $$p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0})= 1/2 \cdot {\rm Q} ( 0.75)+ 1/2 \cdot {\rm Q} ( 1.75)\approx 13.33\% .$$
Hier ist die Verfälschungswahrscheinlichkeit für das Symbol $\boldsymbol{s}_{1}$ ⇒ blaue gefüllte Fläche ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 11.33\%$ aufgrund der ungünstig gewählten Entscheiderschwelle sehr viel größer als die des Symbols $\boldsymbol{s}_{0}$ ⇒ rote gefüllte Fläche ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 2\%$.
On–Off–Keying mit inkohärenter Demodulation
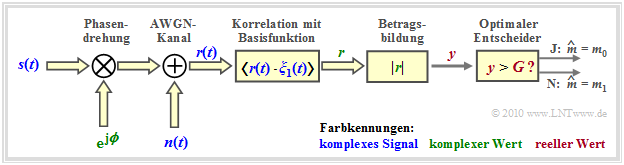
Die folgende Grafik zeigt die Strukur (im äquivalenten Tiefpassbereich) des optimalen OOK–Empfängers für inkohärente Demodulation. Detailbeschreibung
Entsprechend dieser zweiten Grafik gilt:
- Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ am Empfänger ist aufgrund des aktuellen Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex.
- Erforderlich ist nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}(t)$.
- Das Ergebnis ist der (komplexe) Detektorwert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.
- Ist $y \gt G$, so wird als Schätzwert $m_0$ für das Symbol $\boldsymbol{s}_{0}$ ausgegeben, andernfalls der Schätzwert $m_1$ für das Symbol $\boldsymbol{s}_{1}$.
- Auch hier ist die mittlere Symbolfehlerwahrscheinlichkeit als Summe zweier Verbundwahrscheinlichkeiten darstellbar:
- $$p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$$
Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Rayleigh– und Riceverteilung
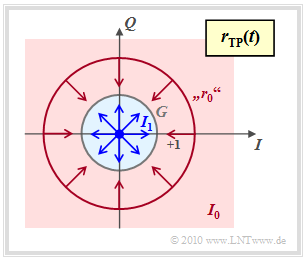
Zur Berechnung der Symbolfehlerwahrscheinlichkeit bei inkohärenter Demodulation gehen wir von folgender Grafik aus. Dargestellt ist das Empfangssignal im äquivalenten Tiefpassbereich in der komplexen Ebene.
- Der Punkt $\boldsymbol{s_1}=0$ führt im Empfangsignal wieder zu $\boldsymbol{r_1}=0$.
- Dagegen kann $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ auf jedem Punkt eines Kreises mit Radius $1$ liegen, da die Phase $\phi$ unbekannt ist.
- Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun zweidimensional zu interpretieren, wie durch die Pfeile in der Grafik angedeutet.
- Die Entscheidungsregion $I_1$ für das Symbol $\boldsymbol{s_1}$ ist der blau gefüllte Kreis mit Radius $G$, wobei der richtige Wert von $G$ noch zu bestimmen ist.
- Liegt der Empfangswert $\boldsymbol{r}$ außerhalb dieses Kreises also im rot hinterlegten Gebiet $I_0$, so fällt die Entscheidung zugunsten von $\boldsymbol{s_0}$.
$\rm Rayleigh–Anteil$
Unter Berücksichtigung des AWGN–Rauschens gilt $\boldsymbol{r_1}=\boldsymbol{s_1} + \boldsymbol{n_1}$. Die Rauschkomponente $\boldsymbol{n_1}$ besitzt eine Rayleighverteilung $($Betrag der beiden mittelwertfreien Gaußkomponenten für $I$ und $Q)$.
Deren bedingte WDF lautet mit der rotationssymmetrischen Rauschkomponente $\eta$ mit $\sigma=\sigma_{\rm AWGN}$ :
- $$f_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1})=\frac{\eta}{\sigma^2}\cdot {\rm e}^{-\eta^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma^2) } = f_{\rm Rayleigh}(\eta) .$$
Damit erhält man für die bedingte Wahrscheinlichkeit
- $${\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1}) = \int_{G}^{\infty}f_{\rm Rayleigh}(\eta) \,{\rm d} \eta \hspace{0.05cm},$$
und mit dem Faktor $1/2$ wegen der gleichwahrscheinlichen Sendesymbole die Verbundwahrscheinlichkeit:
- $${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) = 1/2 \cdot {\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1})= 1/2 \cdot \int_{G}^{\infty}f_{\rm Rayleigh}(\eta) \,{\rm d} \eta \hspace{0.05cm}.$$
$\rm Rice–Anteil$
Die Rauschkomponente $\boldsymbol{n_0}$ besitzt eine Riceverteilung $($Betrag der Gaußkomponenten mit Mittelwerten $m_x$ und $m_y)$ ⇒ Konstante $C=\sqrt{m_x^2 + m_y^2}$
$($Anmerkung: Im Applet wird die Konstante $C$ mit $C_{\rm Rice}$ bezeichnet$)$.
- $$f_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) = f_{\rm Rice}(\eta) \hspace{1.4cm}{\rm mit} \hspace{1.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$
Damit ergibt sich für die zweite Verbundwahrscheinlichkeit:
- $${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) = 1/2 \cdot \int_{0}^{G}f_{\rm Rice}(\eta) \,{\rm d} \eta \hspace{0.05cm}.$$
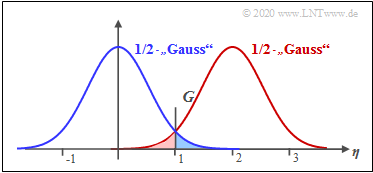
$\text{Beispiel 2:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_{\rm AWGN} = 0.5$ und $C_{\rm Rice} = 2$. Die Entscheidungsgrenze liegt bei $G \approx 1.25$. Man erkennt aus dieser Darstellung:
- Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. Wie im Beispiel 1 für den kohärenten Fall gilt auch hier:
- $$p_{\rm S} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) + {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}).$$
- Die blau markierte Fläche gibt die Verbundwahrscheinlichkeit ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 2.2\%$ an. Diese berechnet sich als das Integral über die halbe Rayleigh–WDF im Bereich von $G$ bis $\infty$.
- Die rot markierte Fläche gibt die Verbundwahrscheinlichkeit ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 2.4\%$ an. Diese berechnet sich als das Integral über die halbe Rice–WDF im Bereich von $0$ bis $G$.
- Somit erhält man $p_{\rm S} \approx 4.6\%$. Anzumerken ist, dass die roten und blauen Flächen nicht gleich sind und dass sich die optimale Entscheidungsgrenze $G_{\rm opt}$ sich aus dem Schnittpunkt der beiden Kurven ergibt.
- Die optimale Entscheidungsgrenze $G_{\rm opt}$ ergibt sich als der Schnittpunkt von blauer und roter Kurve.
Versuchsdurchführung
- Wählen Sie die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe. Die Nummer „$0$” entspricht einem „Reset”: Einstellung wie beim Programmstart.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”.
- Interpretieren Sie stets die Grafiken und die numerischen Ergebnisse. Die Symbole $s_0$ (einstellbar) und ${s}_{1}\equiv 0$ seien gleichwahrscheinlich.
- Aus Platzgründen verwenden wir bei den folgenden Fragen und Musterlösungen teilweise auch $\sigma = \sigma_{\rm AWGN}$ und $C = C_{\rm Rice}$.
(1) Wir betrachten die kohärente Demodulation mit $\sigma_{\rm AWGN} = 0.5$ und $s_0 = 2$. Was ist der kleinstmögliche Wert für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$?
- Bei kohärenter Demodulation setzt sich die WDF des Empfangssignals aus zwei „halben” Gaußfunktionen um $s_0 = 2$ $($rot$)$ und $s_1 = 0$ $($blau$)$ zusammen.
- Der minimale $p_{\rm S}$–Wert ergibt sich hier mit $G=1$ sowie $\Delta G = s_{0} -G= G-s_1 = 1$ zu $p_{\rm S}= {\rm Q} ( \Delta G/\sigma )={\rm Q} ( 1/0.5 )= {\rm Q} ( 2 )\approx 2.28 \%.$
- Mit $G=1$ werden beide Symbole gleich verfälscht. Die blaue Fläche ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1})$ ist gleich der roten Fläche ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0})$. Deren Summe ergibt $p_{\rm S}$.
- Mit $G=0.5$ ist zwar die rote Fläche nahezu Null. Trotzdem ist $p_{\rm S}\approx 8\%$ (Summe beider Flächen) mehr als doppelt so groß als mit $G_{\rm opt}=1$.
(2) Nun gelte $\sigma = 0.75$. Mit welchem $s_0$–Wert ergibt sich bei optimalem $G$ die gleiche Fehlerwahrscheinlichkeit wie in $(1)$? Wie groß ist dann der Quotient $E_{\rm S}/N_0$?
- Allgemein gilt $p_{\rm S}= {\rm Q}\big ( (s_0/2) / \sigma \big )$. Erhöht man $\sigma$ von $0.5$ auf $0.75$, dann muss auch $s_0$ erhöht werden ⇒ $s_0 = 3$ ⇒ $p_{\rm S}= {\rm Q} ( 1.5/ 0.75 )= {\rm Q} ( 2 )$.
- Außer $p_{\rm S}= {\rm Q}\big ( (s_0/2) / \sigma \big )$ gilt aber auch: $p_{\rm S}= {\rm Q} ( \sqrt{E_{\rm S}/N_0} )$. Daraus folgt: $p_{\rm S}= {\rm Q}(2) ={\rm Q} ( \sqrt{E_{\rm S}/N_0})$ ⇒ $\sqrt{E_{\rm S}/N_0}= 2$ ⇒ $E_{\rm S}/N_0= 4$.
- Zur Kontrolle: $E_{\rm S}=s_0^2/2 \cdot T, \ N_0=2T \cdot \sigma^2$ ⇒ $E_{\rm S}/N_0 =s_0^2/(4 \cdot \sigma^2)= 3^2/(4 \cdot 0.75^2)=4$. Das gleiche $E_{\rm S}/N_0 =4$ ergibt sich für die Aufgabe (1).
(3) Nun betrachten wir die inkohärente Demodulation mit $\sigma_{\rm AWGN} = 0.75$, $C_{\rm Rice} = 2.25$ und $G=2$. Wie groß ist die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$?
- Bei inkohärenter Demodulation setzt sich die WDF des Empfangssignals aus einer „halben” Rayleighfunktion $($blau$)$ und einer „halben” Ricefunktion $($rot$)$ zusammen.
- ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 1.43\%$ gibt die Anteile der blauen Kurve oberhalb von $G =2$ an, und ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 15.18\%$ die Anteile der roten Kurve unterhalb von $G =2$.
- Mit $G=2$ ergibt sich für die Symbolfehlerwahrscheinlichkeit die Summe $p_{\rm S}\approx 16.61\%$ , und mit $G_{\rm opt}=1.58$ ein geringfügig besserer Wert: $p_{\rm S}\approx 12.25\%$.
(4) Es sei $X$ allgemein eine Rayleigh–Zufallsgröße und $Y$ eine Rice–Zufallsgröße, jeweils mit obigen Parametern. Wie groß sind ${\rm Pr}(X\le 2)$ und ${\rm Pr}(Y\le 2)$ ?
- Es gilt ${\rm Pr}(Y\le 2) = 2 \cdot {\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 30.36\%$, da im Programm die Rice–WDF mit dem Faktor $1/2$ dargestellt ist.
- In gleicher Weise gilt ${\rm Pr}(X> 2) = 2 \cdot {\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 2.86\%$ ⇒ ${\rm Pr}(X \le 2)= 1-0.0286 = 97.14\%$.
(5) Wir betrachten die Werte $\sigma_{\rm AWGN} = 0.75$, $C_{\rm Rice} = 2.25$ und $G=G_{\rm opt}=1.58$. Wie ändert sich $p_{\rm S}$, wenn man „Rice” bestmöglich durch „Gauß” ersetzt?
- Nach der exakten Berechnung ergibt sich mit der optimalen Schwelle $G_{\rm opt}=1.58$: ${\rm Pr}(\boldsymbol{r_0} \cap \boldsymbol{s_1}) \approx 5.44\%$, ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 6.81\%$ ⇒ $p_{\rm S}\approx 12.25\%$.
- Mit der Gaußnäherung wird bei gleichem $G$ der erste Term nicht verändert. Der zweite Term erhöht sich auf ${\rm Pr}(\boldsymbol{r_1} \cap \boldsymbol{s_0}) \approx 9.29\%$ ⇒ $p_{\rm S}\approx 14.73\%$.
- Die neue Optimierung des Schwellenwerts $G$ unter Berücksichtigung der Gaußnäherung führt auf $G_{\rm opt}=1.53$ und $p_{\rm S}\approx 14.67\%$.
- Die Parameter der Gaußverteilung sind dabei wie folgt einzustellen: Mittelwert $m_{\rm Gauß}= C_{\rm Rice}=2.25$, Streuung $\sigma_{\rm Gauß}= \sigma_{\rm AWGN}=0.75$.
(6) Wie ändern sich die Ergebnisse gegenüber $(5)$ mit $\sigma_{\rm AWGN} = 0.5$, $C_{\rm Rice} = 1.5$ bzw. mit $\sigma_{\rm AWGN} = 1$, $C_{\rm Rice} = 3$, jeweils mit $G=G_{\rm opt}$?
- Bei optimaler Entscheidungsgrenze ergeben sich stets gleiche Wahrscheinlichkeiten, sowohl für die exakte Riceverteilung als auch mit der Gaußnäherung.
- Bei allen drei Parametersätzen gilt $E_{\rm S}/N_0= 2.25$. Dies lässt vermuten: die Ergebnisse bei inkohärenter Demodulation hängen allein von dieser Kenngröße ab.
(7) Die Einstellung sei weiterhin „inkohärent mit Näherung”. Es gelte stets $C_{\rm Rice} = 3$, $G=G_{\rm opt}$. Variierern Sie die AWGN–Streuung im Bereich $0.5 \le \sigma \le 1$.
Interpretieren Sie den relativen Fehler „Falsch minus Richtig/Richtig” in Abhängigkeit der Kenngröße $E_{\rm S}/N_0$.
- Mit $\sigma =0.5$ ⇒ $E_{\rm S}/N_0 = 9$ erhält man $p_{\rm S}^{\ \rm exakt}\approx 0.32\%$ und $p_{\rm S}^{\ \rm Näherung}\approx 0.38\%$. Der absolute Fehler beträgt $0.06\%$ und der relative Fehler $18.75\%$.
- Mit $\sigma =1$ ⇒ $E_{\rm S}/N_0 = 2.25$ erhält man $p_{\rm S}^{\ \rm exakt}\approx 12.25\%$ und $p_{\rm S}^{\ \rm Näherung}\approx 14.67\%$. Der absolute Fehler beträgt $2.42\%$ und der relative Fehler $19.75\%$.
- Fazit: Die Gaußnäherung wird mit größerem $E_{\rm S}/N_0$ immer besser. Diese Aussage erkennt man am absoluten Fehler deutlicher als am relativen Fehler.
(8) Wiederholen Sie den letzten Versuch nun mit der Einstellung „kohärent” sowie $s_0 = 3$, $G=G_{\rm opt}$. Welches Fazit erlaubt der Vergleich mit (7)?
- Der Vergleich von $(7)$ und $(8)$ zeigt: Für jedes $E_{\rm S}/N_0$ ergibt sich bei inkohärenter Demodulation eine größere Symbolfehlerwahrscheinlichkeit.
- Für $E_{\rm S}/N_0= 9$ ergibt sich $p_{\rm S}^{\ \rm kohärent}\approx 0.13\%$ und $p_{\rm S}^{\ \rm inkohärent}\approx 0.32\%$. Und für $E_{\rm S}/N_0= 2.25$ erhält man $p_{\rm S}^{\ \rm kohärent}\approx 6.68\%$ und $p_{\rm S}^{\ \rm inkohärent}\approx 12.25\%$.
- Die einfachere Realisierung des inkohärenten Demodulators (keine Taktsynchronisierung) bewirkt einen Qualitätsverlust ⇒ größere Fehlerwahrscheinlichkeit.
Zur Handhabung des Applets
(A) Auswahl:
- Kohärent,
- inkohärent,
- inkohärent mit Näherung.
(B) Parametereingabe:
- $\sigma_{\rm AWGN}$,
- $s_0$,
- $E_{\rm S}/N_0$,
- $G_{\rm opt}$
(C) Numerischer Ausgabebereich der Wahrscheinlichkeiten
(D) Grafischer Ausgabebereich der WDF-Anteile
(E) Aufgabenauswahl
(F) Fragen und Lösungen
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2011 von Martin Völkl im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
- 2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5/JS” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
- Diese Umsetzung wurde von der Fakultät Elektrotechnik & Informationstechnik der TU München durch "Studienzuschüsse" finanziell unterstützt. Wir bedanken uns.