Diskrete Fouriertransformation und Inverse
!!! Diese App wird gerade entwickelt. Entwicklungsstufe 0. Hat mit dem angekündigten Thema noch nichts zu tun!!!
Inhaltsverzeichnis
Programmbeschreibung
Das Applet verdeutlicht die Eigenschaften zweidimensionaler Gaußscher Zufallsgrößen $XY\hspace{-0.1cm}$, gekennzeichnet durch die Standardabweichungen (Streuungen) $\sigma_X$ und $\sigma_Y$ ihrer beiden Komponenten sowie den Korrelationskoeffizienten $\rho_{XY}$ zwischen diesen. Die Komponenten werden als mittelwertfrei vorausgesetzt: $m_X = m_Y = 0$.
Das Applet zeigt
- die zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{XY}(x, \hspace{0.1cm}y)$ in dreidimensionaler Darstellung sowie in Form von Höhenlinien,
- die zugehörige Randwahrscheinlichkeitsdichtefunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{X}(x)$ der Zufallsgröße $X$ als blaue Kurve; ebenso $f_{Y}(y)$ für die zweite Zufallsgröße,
- die zweidimensionale Verteilungsfunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{XY}(x, \hspace{0.1cm}y)$ als 3D-Plot,
- die Verteilungsfunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{X}(x)$ der Zufallsgröße $X$; ebenso $F_{Y}(y)$ als rote Kurve.
Das Applet verwendet das Framework Plot.ly
Theoretischer Hintergrund
Diskrete Fouriertransformation
Aus dem herkömmlichen „ersten Fourierintegral”
- $$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion
- $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind.
Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor:
- Die $N$ Zeitbereichskoeffizienten seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Die $N$ Frequenzbereichskoeffizienten seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1:
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abkürzend wird für den von $N$ abhängigen komplexen Drehfaktor geschrieben:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
$\text{Definition:}$
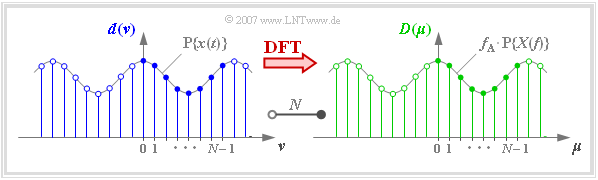
Unter dem Begriff Diskrete Fouriertransformation (kurz DFT) versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
In der Grafik erkennt man an einem Beispiel
- die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung,
- die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.
Inverse Diskrete Fouriertransformation
Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das „zweite Fourierintegral”
- $$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in diskretisierter Form: $d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$
$\text{Definition:}$
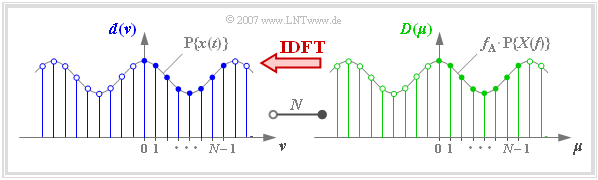
Unter dem Begriff Inverse Diskrete Fouriertransformation (kurz IDFT) versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$
- $$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$
Ein Vergleich zwischen DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind:
- Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen.
- Bei der IDFT entfällt die Division durch $N$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Bei der Aufgabenbeschreibung verwenden wir $\rho$ anstelle von $\rho_{XY}$.
- Für die „1D-WDF” gilt: $f_{X}(x) = \sqrt{1/(2\pi \cdot \sigma_X^2)} \cdot {\rm e}^{-x^2/(2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sigma_X^2)}$.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Neue Einstellung: $\text{DFT von Signal (a): Gleichsignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen FT?
- Im Zeitbereich sind alle $d(\nu) =1$. Dann sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(0)] =1$.
- Dies entspricht bei der herkömmlichen (zeitkontinuierlichen) Fouriertransformation: $x(t) = A\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = A \cdot \delta(f=0)$ mit $A=1$.
(2) Gehen Sie vom erhaltenen $D(\mu)$–Feld aus und verschieben Sie alle Koeffizienten um eine Stelle nach unten. Welche Zeitfunktion liefert die $\rm IDFT$?
- Nun sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Das Zeitbereichsergebnis ist eine komplexe Exonentialfunktion.
- Der Realteil des $d(\nu)$–Feldes zeigt einen Cosinus und der Imaginärteil eine Sinusfunktion. Bei beiden Funktionen erkennt man jeweils eine Periode.
(3) Ergänzen Sie das aktuelle $D(\mu)$–Feld um den Koeffizienten ${\rm Im}\big [D(1)] =1$. Welche Unterschiede erkennt man gegenüber (2) im Zeitbereich?
- Zum einen erkennt man nun bei Realteil und Imaginärteil eine Phasenverschiebung um zwei Stützwerte. Dies entspricht der Phase $\varphi = 45^\circ$.
- Zudem wurden die Amplituden von Real– und Imaginärteil jeweils um den Faktor $\sqrt{2}$ vergrößert.
(4) Setzen Sie das $D(\mu)$–Feld auf Null mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Durch welchen zusätzlichen $D(\mu)$–Koeffizienten erhält man ein reelles $d(\nu)$–Feld?
- Durch Probieren oder Nachdenken erkennt man, dass auch ${\rm Re}\big [D(15)] =1$ gesetzt werden muss. Dann beschreibt das $d(\nu)$–Feld einen Cosinus.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = 2 \cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = \delta(f -f_0)+\delta(f +f_0)$.
- Das Feld $D(1)$ steht für die Frequenz $f_0$ und aufgrund der Periodizät mit $N=16$ wird die Frequenz $-f_0$ durch $D(15) = D(-1)$ ausgedrückt.
(5) Mit welchem $D(\mu)$–Feld erhält man nach der $\rm IDFT$ im $d(\nu)$–Feld eine reelle Cosinusfunktion mit der Amplitude $A=1$?
- Die Diskrete Fouriertransformation ist ebenso wie die herkömmliche Fouriertransformation linear ⇒ $D(1) = D(15)=0.5$.
(6) Neue Einstellung: $\text{DFT von Signal (e): Cosinussignal}$ und anschließende Signalverschiebungen. Was bewirken diese Verschiebungen im Frequenzbereich?
- Eine Verschiebung im Zeitbereich verändert das Cosinussignal zu einer „Harmonischen Schwingung” mit beliebiger Phase.
- Das $D(\mu)$–Feld ist weiterhin Null bis auf $D(1)$ und $D(15)$. Die Beträge $|D(1)|$ und $|D(15)|$ bleiben ebenfalls gleich.
- Die alleinige Veränderung betrifft die Phase, also die unterschiedliche Aufteilung der Beträge auf Real– und Imaginärteil.
(7) Neue Einstellung: $\text{DFT von Signal (f): Sinussignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen FT?
- Das Sinussignal ergibt sich aus dem Cosinussignal durch vier Zeitverschiebungen. Deshalb gelten alle Aussagen von (6) weiterhin.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = {\rm j}/2 \cdot \big [\delta(f +f_0)-\delta(f -f_0)\big ]$.
- Der Koeffizient $D(1)$ ⇒ $($Frequenz: $+f_0)$ ist imaginär und hat den Imaginärteil $-0.5$. Entsprechend gilt ${\rm Im}\big [D(15)] =+0.5$ ⇒ $($Frequenz: $-f_0)$.
(8) Neue Einstellung: $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$. Interpretieren Sie das Ergebnis im Vergleich zur Aufgabe (5).
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (2f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -2 f_0)+0.5 \cdot \delta(f +2f_0)$.
- Für die Frequenz $2f_0$ steht das Feld $D(2)$ und für die Frequenz $-2f_0$ aufgrund der Periodizät das Feld $D(14) = D(-2)$ : $D(2) = D(14) = 0.5$.
(9) Untersuchen Sie nun den Fall $\text{DFT von Sinussignal (zwei Perioden)}$. Welche Einstellung müssen Sie vornehmen? Interpretieren Sie das Ergebnis.
- Zum gewünschten Signal kommt man von $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$ mit zwei Verschiebungen. Bei (7): Vier Verschiebungen.
- Das DFT–Ergebnis lautet dementsprechend: ${\rm Im}\big [D(2)] =-0.5$ und ${\rm Im}\big [D(14)] =+0.5$.
(10) Neue Einstellung: $\text{DFT von (h) Alternierende Zeitkoeffizienten}$. Interpretieren Sie das DFT–Ergebnis.
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (8f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -8 f_0)+0.5 \cdot \delta(f +8f_0)$.
- $8f_0$ ist die höchste mit $N=16$ in der DFT darstellbare Frequenz. Pro Periodendauer gibt es nur zwei Abtastwerte, nämlich $+1$ und $-1$.
- Unterschied zur Teilaufgabe (5): Aus $D(1) =0.5$ wird nun $D(8) =0.5$. Ebenso verschiebt sich $D(15) =0.5$ auf $D(8) =0.5$. Endergebnis: $D(8) =1$.
(11) Welche Unterschiede erhält man mit den beiden Einstellungen $\text{IDFT von Spektrum (C)}$ sowie $\text{DFT von Signal (c)}$ ?
- Im ersten Fall ⇒ ${\rm Re}\big [D(\mu=1)] = 1$ ergibt sich im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit positivem Vorzeichen.
- Im zweiten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen.
- Für ${\rm Re}\big [d(\nu=15)] = 1$ würde sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit positivem Vorzeichen ergeben.
(12) Neue Einstellung: $\text{DFT von Signal (k) Dreieckimpuls}$. Interpretieren Sie die $d(\nu)$–Belegung und das DFT–Ergebnis.
- Wählen Sie die Betragsdarstellung. $x(t)$ ist symmetrisch um $t=0$ und erstreckt sich von $-T/2$ bis $+T/2$. Es gilt $T_{\rm A} = T/16$. $d(\nu)$–Belegung:
- $d(0)=x(0)= 1$, $d(1)=x(T_{\rm A})= 0.875$, ... , $d(8)=x(8T_{\rm A})= 0$, $d(9)=x(-7T_{\rm A})= 0.125$, ..., $d(15)=x(-T_{\rm A})= 0.875$.
- Im Frequenzbereich: Erst Gleichanteil ⇒ $D(0)$, dann positive Frequenzen ⇒ $D(1) ,\text{ ... },D(8)$, dann negative Frequenzen (gespiegelt) ⇒ $D(9), \text{ ... },D(15)$.
Zur Handhabung des Applets
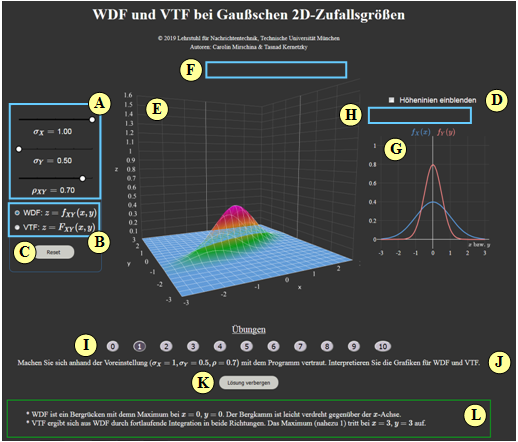
(A) Parametereingabe per Slider: $\sigma_X$, $\sigma_Y$ und $\rho$
(B) Auswahl: Darstellung von WDF oder VTF
(C) Reset: Einstellung wie beim Programmstart
(D) Höhenlinien darstellen anstelle von „1D-WDF”
(E) Darstellungsbereich für „2D-WDF”
(F) Manipulation der 3D-Grafik (Zoom, Drehen, ...)
(G) Darstellungsbereich für „1D-WDF” bzw. „Höhenlinien”
(H) Manipulation der 2D-Grafik („1D-WDF”)
( I ) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
(K) Bereich für die Versuchsdurchführung: Musterlösung einblenden
( L) Bereich für die Versuchsdurchführung: Musterlösung
Werte–Ausgabe über Maussteuerung (sowohl bei 2D als auch bei 3D)
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.