Optimale Empfängerstrategien
Betrachtetes Szenario im Kapitel 3.7
Alle bisher beschriebenen Digitalempfänger treffen stets symbolweise Entscheidungen. Werden dagegen mehrere Symbole gleichzeitig entschieden, so können bei der Detektion statistische Bindungen zwischen den Empfangssignalabtastwerten berücksichtigt werden, was eine geringere Fehlerwahrscheinlichkeit zur Folge hat – allerdings auf Kosten einer zusätzlichen Laufzeit.
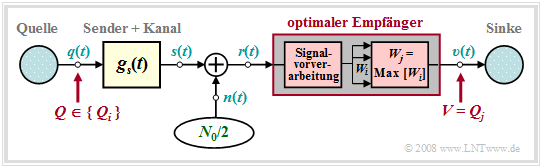
In diesem – teilweise auch im nächsten Kapitel – wird von folgendem Übertragungsmodell ausgegangen:
Gegenüber den letzten Kapiteln 3.5 und 3.6 ergeben sich folgende Unterschiede:
- Q ∈ {Qi} mit i = 0, ... , M–1 bezeichnet eine zeitlich begrenzte Quellensymbolfolge 〈qν〉, deren Symbole vom optimalen Empfänger gemeinsam entschieden werden sollen.
- Beschreibt Q eine Folge von N redundanzfreien Binärsymbolen, so ist M = 2N zu setzen. Dagegen gibt M bei symbolweiser Entscheidung die Stufenzahl der digitalen Quelle an.
- Im obigen Modell werden eventuelle Kanalverzerrungen dem Sender hinzugefügt und sind somit bereits im Grundimpuls gs(t) und im Signal s(t) enthalten. Diese Maßnahme dient lediglich einer einfacheren Darstellung und stellt keine Einschränkung dar.
- Der optimale Empfänger sucht unter Kenntnis des aktuell anliegenden Empfangssignals r(t) aus der Menge {Q0, ... , QM–1} der möglichen Quellensymbolfolgen die am wahrscheinlichsten gesendete Folge {Qj} und gibt diese als Sinkensymbolfolge V aus.
- Vor dem eigentlichen Entscheidungsalgorithmus muss durch eine geeignete Signalvorverarbeitung aus dem Empfangssignal r(t) für jede mögliche Folge Qi ein Zahlenwert Wi abgeleitet werden. Je größer Wi ist, desto größer ist die Rückschlusswahrscheinlichkeit, dass Qi gesendet wurde.
- Die Signalvorverarbeitung muss für die erforderliche Rauschleistungsbegrenzung und – bei starken Kanalverzerrungen – für eine ausreichende Vorentzerrung der entstandenen Impulsinterferenzen sorgen. Außerdem beinhaltet die Vorverarbeitung auch die Abtastung zur Zeitdiskretisierung.
MAP– und Maximum–Likelihood–Entscheidungsregel (1)
Man bezeichnet den (uneingeschränkt) optimalen Empfänger als MAP–Empfänger, wobei „MAP” für „Maximum–a–posteriori” steht.
Die Rückschlusswahrscheinlichkeit Pr(Qi|r(t)) gibt an, mit welcher Wahrscheinlichkeit die Folge Qi gesendet wurde, wenn das Empfangssignal r(t) am Entscheider anliegt. Mit dem Satz von Bayes kann diese Wahrscheinlichkeit wie folgt berechnet werden:
\[{\rm Pr}(Q_i \hspace{0.05cm}|\hspace{0.05cm} r(t)) = \frac{ {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \cdot {\rm Pr}(Q_i)}{{\rm Pr}(r(t))} \hspace{0.05cm}.\]
Die MAP–Entscheidungsregel lässt sich somit wie folgt umformulieren bzw. vereinfachen. Man setze die Sinkensymbolfolge V = Qj, falls für alle i ≠ j gilt:
\[\frac{ {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_j) \cdot {\rm Pr}(Q_j)}{{\rm Pr}(r(t))} > \frac{ {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \cdot {\rm Pr}(Q_i)}{{\rm Pr}(r(t))}\]
\[\Rightarrow \hspace{0.3cm} {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_j) \cdot {\rm Pr}(Q_j)> {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \cdot {\rm Pr}(Q_i) \hspace{0.05cm}.\]
Eine weitere Vereinfachung dieser MAP–Entscheidungsregel führt zum ML–Empfänger, wobei „ML” für „Maximum–Likelihood” steht.
\[{\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_j) > {\rm Pr}( r(t)\hspace{0.05cm}|\hspace{0.05cm} Q_i) \hspace{0.05cm}.\]
Ein Vergleich dieser beiden Definitionen zeigt, dass bei gleichwahrscheinlichen Quellensymbolen der ML– und der MAP–Empfänger gleiche Entscheidungsregeln befolgen und somit vollkommen äquivalent sind. Bei nicht gleichwahrscheinlichen Symbolen ist der ML– dem MAP–Empfänger unterlegen, da er für die Detektion nicht alle zur Verfügung stehenden Informationen nutzt.