Aufgabe 1.7Z: BARBARA-Generator

• Zurück zum Buch

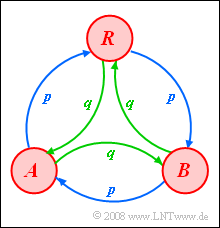
Betrachtet wird hier ein ternärer Zufallsgenerator mit den Symbolen $A$, $B$ und $R$, der durch eine homogene und stationäre Markovkette erster Ordnung beschrieben werden kann.

Die Übergangswahrscheinlichkeiten können dem skizzierten Markovdiagramm entnommen werden. Für die Teilaufgaben a) bis c) soll stets $p = 1/4$ gelten.

Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 1.4.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Die Werte von $p > 0$ und $q < 1$ sind weitgehend frei wählbar.
	Für die Übergangswahrscheinlichkeiten muss gelten: $p + q = 1$.
	Alle Symbole haben gleiche ergodische Wahrscheinlichkeiten.
	Es gilt hier: $Pr(A) = 1/2, Pr(B) = 1/3, Pr(R) = 1/6$.

2

Wie groß sind die bedingten Wahrscheinlichkeiten $p_A$, $p_B$ und $p_R$, dass zu den Zeiten $ν+1, ... , ν+7$ „BARBARA” ausgegeben wird, wenn man sich zum Zeitpunkt ν im Zustand $A$, $B$ bzw. $R$ befindet? Es gelte $p = 1/4$.

$p_A$ = $* 10^{}$ ^

$p_B$ =

$p_R$ = $* 10^{}$ ^

3

Wie groß ist die Wahrscheinlichkeit insgesamt, dass der Generator zu sieben aufeinanderfolgenden Zeitpunkten BARBARA ausgibt $(p = 1/4)$?

$Pr(BARBARA)$ = $* 10^{}$ ^

4

Wie ist der Parameter $p$ zu wählen, damit $Pr(BARBARA)$ möglichst groß wird? Welche Wahrscheinlichkeit ergibt sich damit für BARBARA?

$p$ =

$Pr(BARBARA)$ =

Musterlösung

Musterlösung

a)

b)

c)

d)

e)

f)

g)