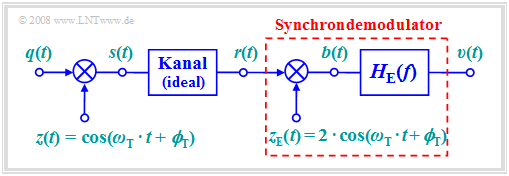
Synchrondemodulation

Blockschaltbild und Zeitbereichsdarstellung

Eine Modulation am Sender macht nur Sinn, wenn es möglich ist, diese Signalumsetzung am Empfänger wieder rückgängig zu machen und zwar möglichst ohne Informationsverlust.

Bei jeder Form von Amplitudenmodulation (sei es ZSB oder ESB, mit oder ohne Träger) erfüllt der so genannte Synchrondemodulator diese Aufgabe. Zu obigem Blockschaltbild ist Folgendes anzumerken:

Zur Modulation wird beispielhaft ZSB–AM ohne Träger (Modulationsgrad $m → ∞$ ) betrachtet. Synchrondemodulation ist aber auch anwendbar, wenn der Träger in $s(t)$ enthalten ist.
Der Kanal sei ideal und die Störungen vernachlässigbar, so dass das Empfangssignal $r(t)$ identisch mit dem Sendesignal $s(t)$ ist:

$r(t) = s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.$

Im Empfänger wird dieses Signal zunächst mit dem empfängerseitigen Trägersignal

$z_{\rm E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \phi_{\rm T})$

multipliziert, das bis auf den Faktor 2 identisch mit dem sendeseitigen Träger

$z(t)$ ist.

Das Ergebnis der Multiplikation ist das Signal

$\begin{align*}b(t) & = r(t) \cdot z_{\rm E}(t) = 2 \cdot q(t) \cdot \cos^2(\omega_{\rm T} \cdot t + \phi_{\rm T})= \\ & = q(t) + q(t) \cdot \cos(2 \cdot \omega_{\rm T} \cdot t + 2\cdot \phi_{\rm T})\hspace{0.05cm}.\end{align*}$

Hierbei ist die trigonometrische Umformung

$\cos²(α) = 1/2 · (1 + \cos(2α))$ berücksichtigt.

Der zweite Term liegt im Bereich um die doppelte Trägerfrequenz. Ist $f_{\rm T} > B_{\rm NF}$ , was in der Praxis stets zutrifft, so kann dieser Anteil durch einen geeignet dimensionierten Tiefpass $H_{\rm E}(f)$ unterdrückt werden, und man erhält $υ(t) = q(t)$ .