Aufgabe 3.3Z: Rechteck- und Diracimpuls
Wir betrachten hier eine Vielzahl von symmetrischen Rechteckfunktionen $x_k(t)$. Die einzelnen Rechtecke unterscheiden sich durch unterschiedliche Amplituden (Höhen)
- $$A_k = k \cdot A$$
und unterschiedliche Impulsdauern (Breiten)
- $$T_k = T/k.$$
Hierbei sei $k$ ein beliebiger positiver Wert.
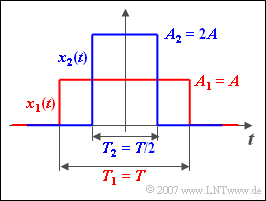
- Der im Bild rot dargestellte Rechteckimpuls $x_1(t)$ hat die Amplitude $A_1 = {A} = 2 \,\text{V}$ und die Dauer $T_1 = {T} = 500 \,µ\text{s}$.
- Der blau gezeichnete Impuls $x_2(t)$ ist halb so breit ⇒ $T_2 =250 \,µ\text{s}$, aber doppelt so hoch ⇒ $A_2 = 4 \text{ V}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Sonderfälle impulsartiger Signale.
- Sie können Ihre Ergebnisse anhand der beiden interaktiven Applets Impulse und Spektren sowie Frequenzgang und Impulsantwort überprüfen.
Fragebogen
Musterlösung
- Der Spektralwert bei der Frequenz $f = 0$ ist nach dem ersten Fourierintegral stets gleich der Fläche unter der Zeitfunktion:
- $$X( f ) = \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm{e}}^{ - {\rm{j2\pi }}ft} \hspace{0.1cm} {\rm d}t \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \;X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t )}\hspace{0.1cm} {\rm d}t.$$
- Im vorliegenden Fall ist die Impulsfläche stets $A \cdot T = 10^{–3} \,\text{Vs} = 1\, \text{mV/Hz}$.
- Wegen $T_1 = 500 \,\mu\text{s}$ weist das Spektrum $X_1(f)$ Nulldurchgänge im Abstand $f_1 = 1/T_1 = 2 \,\text{kHz}$ auf.
(2) Richtig sind die Lösungsvorschläge 1 und 3:
- Aufgrund gleicher Impulsflächen wird der Spektralwert bei der Frequenz $f = 0$ nicht verändert.
- Die äquidistanten Nulldurchgänge treten nun im Abstand $f_2 = 1/T_2 = 4 \,\text{kHz}$ auf.
(3) Nullstellen gibt es bei Vielfachen von $f_{10} = 1/T_{10} = 20 \,\text{kHz}$, und die Spektralfunktion lautet:
- $$X_{10} ( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}f/f_{10} } ).$$
Bei der Frequenz $f = 2 \,\text{kHz}$ ist das Argument der si-Funktion gleich $\pi/10$ (oder $18^{\circ}$):
- $$X_{10} ( {f = 2\;{\rm{kHz}}}) = 10^{ - 3} \;{\rm{V/Hz}} \cdot \frac{{\sin ( {18^\circ } )}}{{{\rm{\pi /10}}}} \hspace{0.15 cm}\underline{= 0.984 \;{\rm{mV/Hz}}}{\rm{.}}$$
(4) Im Grenzfall $k \rightarrow \infty$ geht der dann unendlich hohe und unendlich schmale Rechteckimpuls in den Diracimpuls über. Dessen Spektrum ist für alle Frequenzen konstant. Damit gilt auch bei der Frequenz $f = 2 \,\text{kHz}$ der Spektralwert $X_{\infty}(f = 2 \,\text{kHz})\underline{=1 \text{mV/Hz}}$.