Aufgabe 2.3: QAM–Signalraumbelegung
Bei ADSL (Asymmetric Digital Subscriber Line) sind verschiedene Übertragungsverfahren anwendbar. Sowohl bei QAM als auch bei CAP und DMT findet dabei eine Signalraumzuordnung statt.
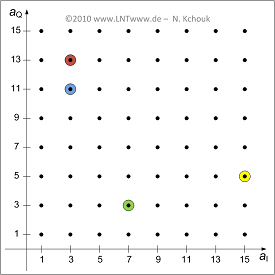
Die Grafik zeigt den ersten Quadranten der betrachteten Signalraumzuordnung. Auf die farblich markierten Punkte wird in der Aufgabe Bezug genommen. Anzumerken ist:
- Die Inphase– und Quadraturkoeffizienten $(a_{\rm I}, a_{\rm Q})$ können hierbei jeweils die Werte $1, 3, ... , 15$ annehmen. In anderen Quadranten sind auch die negativen Werte $–1, –3, ... , –15$ möglich.
- Jeweils $b \rm Bit$ werden zu einem Signalraumpunkt zusammengefasst, der durch die Koordinaten $a_{\rm I}$ und $a_{\rm Q}$ gekennzeichnet wird.
- Wird eine Bitfolge $(q_{b–1}, q_{b–2}, ... , q_{0})$ übertragen, so bezeichnen die MSB (Most Significant Bits) $q_{b–1}$ und $q_{b–2}$ die Vorzeichen von $a_{\rm I}$ und $a_{\rm Q}$, und damit auch den Quadranten.
- Ist $q_{b–1} = 0$, so ist $a_{\rm I}$ positiv. Dagegen weist $q_{b–1} = 1$ auf ein negatives $a_{\rm I}$ hin. Der gleiche Zusammenhang besteht zwischen $q_{b–2}$ und $a_{\rm Q}$.
- Der Inphase–Anteil $a_{\rm I}$ ergibt sich als Dezimalwert der Binärzahl $(q_{b–1}, q_{b–3}, ... , q_{1}, 1)$. Negative Zahlen werden durch das Zweierkomplement dargestellt.
- Der Quadratur–Anteil $a_{\rm Q}$ ergibt sich als Dezimalwert der Binärzahl $(q_{b–2}, q_{b–4}, ... , q_{0}, 1)$. Negative Zahlen werden auch hier durch das Zweierkomplement dargestellt.
Ziel dieser Aufgabe ist es, gegebene Bitfolgen dem richtigen Signalraumpunkt zuzuordnen. Die umgekehrte Zuordnung wird ebenfalls demonstriert.
Hinweis:
Die Aufgabe gehört zum Themengebiet von Kapitel xDSL als Übertragungstechnik.
Fragebogen
Musterlösung
(2) Es muss $2^b = 256$ gelten. Daraus folgt: $\underline{b = 8}$.
(3) Die $\underline{ {\rm MSB} \ \boldsymbol{00}}$ zeigen an, dass $a_{\rm I}$ und $a_{\rm Q}$ positiv sind und markieren somit den hier betrachteten ersten Quadranten. Entsprechend gilt: $\boldsymbol{10}: 2.$ Quadrant, $\boldsymbol{11}: 3$. Quadrant, $\boldsymbol{01}: 4$. Quadrant.
(4) Entsprechend der Angabe ist der Inphasenanteil negativ $(q_{7} = \boldsymbol{1})$. Aus $\boldsymbol{10011}_{\rm binär} = 19_{\rm dez} ergibt sich das Zweierkomplement 19 – 32 = –13. Der Quadraturanteil ergibt sich aus $\boldsymbol{01011}_{\rm binär} = 11:$
- $$\underline{a_{\rm I} = -13,\hspace{0.2cm}a_{\rm Q} = +11} \hspace{0.05cm}.$$
(5)