Mehrwegeempfang beim Mobilfunk
Zeitinvariante Beschreibung des Zweiwegekanals (1)
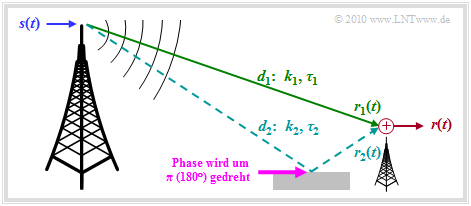
Wir gehen von dem in der Grafik dargestellten Szenario aus. Dabei wird vorausgesetzt:
- Sender und Empfänger sind ruhend. Dann ist sowohl die Kanal–Übertragungsfunktion als auch die Impulsantwort zeitunabhängig. Für alle Zeiten t gilt H(f, t) = H(f) und h(τ, t) = h(τ).
- Ein Zweiwegekanal: Das Sendesignal s(t) erreicht den Empfänger auf direktem Pfad mit der Weglänge d1 und es gibt ein Echo aufgrund des reflektierenden Erdbodens (Distanz d2).
Somit gilt für das Empfangssignal:
r(t)=r1(t)+r2(t)=k1⋅s(t−τ1)+k2⋅s(t−τ2),
wobei die folgenden Aussagen zu beachten sind:
- Das über den Direktpfad empfangene Signal r1(t) ist gegenüber dem Sendesignal s(t) um den Faktor k1 gedämpft und um die Laufzeit τ1 verzögert.
- Der Dämpfungsfaktor k1 wird mit dem Pfadverlustmodell berechnet. k1 ist um so kleiner und der Verlust um so größer, je größer die Sendefrequenz fS, die Distanz d1 und der Exponent γ sind.
- Die Laufzeit τ1 = d1/c nimmt proportional mit der Wegelänge d1 zu. Beispielsweise ergibt sich für die Distanz d1 = 3 km und der Lichtgeschwindigkeit c = 3 · 108 m/s die Verzögerung τ1 = 10 μs.
- Wegen der größeren Weglänge (d2 > d1) weist der zweite Pfad eine größere Dämpfung auf ⇒ |k2| < |k1| und dementsprechend auch eine größere Laufzeit τ2 > τ1.
- Außerdem ist zu berücksichtigen, dass die Reflexion an Gebäuden oder dem Erdboden zu einer Phasendrehung um π (180°) führt. Damit wird der Faktor k2 negativ.
Die Beschreibung wird auf der nächsten Seite fortgesetzt. Das negative Vorzeichen von k2 wird dabei außer Acht gelassen.
Hinweis: Die hier behandelte Thematik wird in folgendem Interaktionsmodul behandelt:
Auswirkungen von Mehrwegeempfang Please add link and do not upload flash videos.
Zeitinvariante Beschreibung des Zweiwegekanals (2)
Für die Frequenzselektivität haben Pfadverlust (gekennzeichnet durch k1) und Grundlaufzeit τ1 keine Bedeutung. Entscheidend sind hier Pfaddverlustunterschiede und Laufzeitdifferenzen. Wir beschreiben nun den Zweiwegekanal mit den neuen Kenngrößen k0 = |k2| / |k1| und τ0 = τ2 – τ1 wie folgt:
r(t)=r1(t)+k0⋅r1(t−τ0)
mitr1(t)=k1⋅s(t−τ1).
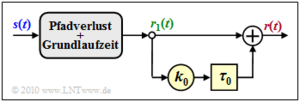
Die Grafik veranschaulicht die Gleichung.
Mit der Vereinfachung k1 = 1, τ1 = 0 ⇒ r1(t) = s(t) erhält man:
r(t)=s(t)+k0⋅s(t−τ0).
Aus diesem vereinfachten Modell (ohne den grau hinterlegten Block in der Grafik) lassen sich wichtige Beschreibungsgrößen einfach berechnen:
- Wendet man den Verschiebungssatz an, so kommt man zur Übertragungsfunktion
- H(f)=R(f)/S(f)=1+k0⋅exp[−j⋅2πf⋅τ0].
- Durch Fourierrücktransformation erhält man dann die Impulsantwort
- h(τ)=1+k0⋅δ(τ−τ0).
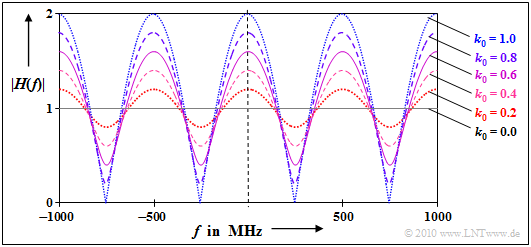
Die Grafik zeigt den Betrag der Übertragungsfunktion im Bereich zwischen ±1000 kHz. Man erkennt aus dieser Darstellung:
- Die Übertragungsfunktion H(f) und auch deren Betrag ist periodisch mit 1/τ0 = 500 kHz. Diese Frequenzperiode ist hier gleichzeitig die sogenannte Kohärenzbandbreite.
- Die Schwankungen um den Mittelwert |H(f)| = 1 sind um so stärker, je größer der (relative) Beitrag k0 des Nebenpfades (also das Echo) ist.