Aufgabe 5.1Z: Abtastung harmonischer Schwingungen
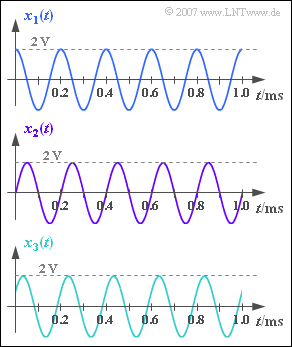
Wir betrachten drei harmonische Schwingungen mit gleicher Frequenz und gleicher Amplitude:
- $$x_1(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_2(t) = A \cdot \sin (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_3(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - 60^{\circ}) \hspace{0.05cm}.$$
Die Schwingungsparameter $f_0$ und $A$ können Sie der Grafik entnehnen.
Angenommen wird, dass die Signale äquidistant zu den Zeitpunkten $\nu \cdot T_{\rm A}$ abgetastet werden, wobei die Parameterwerte $T_{\rm A} = 80 \ \mu \text{s}$ und $T_{\rm A} = 100 \ \mu \text{s}$ analysiert werden sollen.
Die Signalrekonstruktion beim Empfänger erfolgt durch einen Tiefpass $H(f)$, der aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ das Signal $y(t)$ formt. Es gelte:
- $$H(f) = \left\{ \begin{array}{c} 1 \\ 0.5 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_{\rm G} \hspace{0.05cm}, \\ |f| = f_{\rm G} \hspace{0.05cm}, \\ |f| > f_{\rm G} \hspace{0.05cm}, \\ \end{array}$$
Hierbei gibt $f_{\rm G}$ die Grenzfrequenz des rechteckförmigen Tiefpassfilters an. Für diese soll gelten:
- $$f_{\rm G} = \frac{1}{ 2 \cdot T_{\rm A}}\hspace{0.05cm}.$$
Das Abtasttheorem ist erfüllt, wenn $y(t) = x(t)$ gilt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zeitdiskrete Signaldarstellung.
- Zu der hier behandelten Thematik gibt es ein interaktives Applet: Abtastung periodischer Signale & Signalrekonstruktion
Fragebogen
Musterlösung
(2) Richtig sindalle Löungsvorschläge:
- Die Abtastrate ist hier $f_{\rm A} = 1/T_{\rm A} = 12.5 \ \text{kHz}$.
- Dieser Wert ist größer als $2 \cdot f_0 = 10 \ \text{kHz}$.
- Damit ist das Abtasttheorem unabhängig von der Phase erfüllt, und es gilt stets $y(t) = x(t)$.
(3) Die Abtastrate beträgt nun $f_{\rm A} = 2 \cdot f_0 = 10 \ \text{kHz}$. Nur im Sonderfall des Cosinussignals ist nun das Abtasttheorem erfüllt und es gilt:
$y_1(t) = x_1(t)$ ⇒ $A_1 \; \underline{=2 \ \text{V}}$ und $\varphi_1 \; \underline{= 0}.$
Dieses Ergebnis soll nun noch mathematisch hergeleitet werden, wobei im Hinblick auf die noch anstehenden Teilaufgaben bereits auch eine Phase $\varphi$ im Eingangssignal berücksichtigt wird:
- $$x(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - \varphi) \hspace{0.05cm}.$$
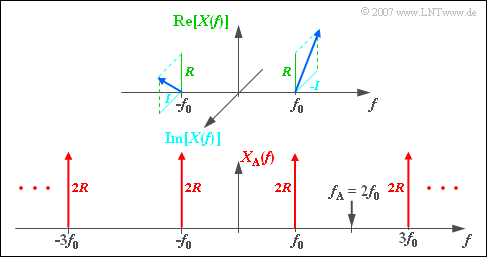
Dann gilt für die Spektralfunktion, die in der oberen Grafik skizziert ist:
- $$X(f) = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f+ f_{\rm 0} ) + {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
Mit den Abkürzungen
- $$R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi) \hspace{0.5cm}{\rm und} \hspace{0.5cm}I ={A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin(\varphi)$$
kann hierfür auch geschrieben werden:
- $$X(f) = (R + {\rm j} \cdot I) \cdot \delta (f+ f_{\rm 0} ) + (R - {\rm j} \cdot I) \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
Das Spektrum des mit $f_{\rm A} = 2f_0$ abgetasteten Signals $x_{\rm A}(t)$ lautet somit:
- $$X_{\rm A}(f) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )= \sum_{\mu = - \infty }^{+\infty} X (f- 2\mu \cdot f_{\rm 0} )\hspace{0.05cm}.$$
- Die untere Grafik zeigt, dass $X_{\rm A}(f)$ aus Diracfunktionen bei $\pm f_0$, $\pm 3f_0$, $\pm 5f_0$, usw. besteht.
- Alle Gewichte sind rein reell und gleich $2 \cdot R$.
- Die Imaginärteile des periodisch fortgesetzten Spektrums heben sich auf.
Berücksichtigt man weiter den rechteckförmigen Tiefpass, dessen Grenzfrequenz exakt bei $f_{\rm G} = f_0$ liegt, sowie $H(f_{\rm G}) = 0.5$, so erhält man für das Spektrum nach der Signalrekonstruktion:
- $$Y(f) = R \cdot \delta (f+ f_{\rm 0} ) + R \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}, \hspace{0.5cm} R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi)\hspace{0.05cm}.$$
Die Fourierrücktransformation führt auf
- $$y(t) = A \cdot \cos (\varphi)\cdot \cos (2 \pi \cdot f_0 \cdot t ) \hspace{0.05cm}.$$
Es ergibt sich also unabhängig von der Eingangsphase $\varphi$ ein cosinusförmiger Verlauf. Ist $\varphi = 0$ wie beim Signal $x_1(t)$, so ist auch die Amplitude des Ausgangssignals gleich $A$.
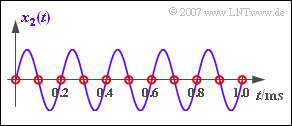
(4) Das Sinussignal hat die Phase $90^\circ$. Daraus folgt direkt $y_2(t) = 0$ ⇒ Amplitude $\underline{A_2 = 0}$.
Dieses Ergebnis wird verständlich, wenn man sich die Abtastwerte in der Grafik betrachtet. Alle Abtastwerte (rote Kreise) sind $0$, so dass auch nach dem Filter kein Signal vorhanden sein kann.
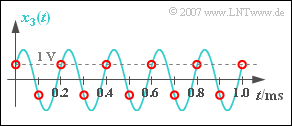
(5) Trotz $\varphi = 60^\circ$ gilt $\varphi_3 = 0$ ⇒ das rekonstruierte Signal $y_3(t)$ ist ebenfalls cosinusförmig. Die Amplitude ist gleich
- $$A_3 = A \cdot \cos (60^{\circ})= {A}/{2} \hspace{0.15 cm}\underline{= 1\,{\rm V}} \hspace{0.05cm}.$$
Wenn Sie die rot eingezeichneten Abtastwerte in der Grafik betrachten, so werden Sie zugeben, dass Sie als „Signalrekonstrukteur” keine andere Entscheidung treffen würden als der Tiefpass, da Sie ja den türkisfarbenen Verlauf nicht kennen.