Aufgabe 3.1Z: Dreieckförmige WDF

• Zurück zum Buch

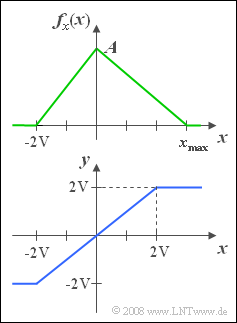
Wir betrachten eine kontinuierliche Zufallsgröße $x$ mit der oben skizzierten WDF. Der Minimalwert des Signals ist $x_{min} = -2\hspace{0.05cm} {\rm V}$. Dagegen ist der maximale Wert $x_{max}$ ein freier Parameter, der Werte zwischen $2\hspace{0.05cm}\rm V$ und $4\hspace{0.05cm} \rm V$ annehmen kann.

Die Zufallsgröße $x$ soll hier als der Momentanwert eines Zufallssignals aufgefasst werden. Gibt man dieses Signal $x(t)$ auf einen Amplitudenbegrenzer mit der Kennlinie (siehe untere Skizze) $$y(t)=\left\{\begin{array}{*{4}{c}} -2\hspace{0.05cm} {\rm V} & {\rm falls}\hspace{0.1cm} x(t)<-2\hspace{0.05cm} {\rm V} , \\ x(t) & {\rm falls}\hspace{0.1cm}-2\hspace{0.05cm} {\rm V} \le x(t)\le +2\hspace{0.05cm} {\rm V}, \\ +2\hspace{0.05cm} {\rm V} & {\rm falls}\hspace{0.1cm} {\it x}({\it t})>+2\hspace{0.05cm} {\rm V}, \\\end{array}\right.$$

so entsteht das Signal $y(t)$ bzw. die neue Zufallsgröße $y$, die in den beiden letzten Teilfragen (5) und (6) betrachtet wird.

Für die Teilaufgaben (1) und (2) gelte $x_{\rm max} = 2\hspace{0.05cm} {\rm V} $; für alle weiteren Teilaufgaben ist $x_{\rm max} = 4\hspace{0.05cm} {\rm V} $ zu setzen.

Hinweise:

• Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichtefunktion.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Eine Zusammenfassung der hier behandelten Thematik bietet das folgende Lernvideo:
  

Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion

Fragebogen

1

Es sei $x_{\rm max} = 2\hspace{0.05cm} {\rm V}$. Berechnen Sie den Parameter $A = f_x(0)$.

$x_{\rm max} = 2\hspace{0.05cm} {\rm V}$:   $A \ =$ $\ \rm 1/V$

2

Mit welcher Wahrscheinlichkeit ist $|x(t)|$ kleiner als $x_{\rm max}/2$?

$x_{\rm max} = 2\hspace{0.05cm} {\rm V}$:   ${\rm Pr}(|x| < 2\hspace{0.05cm} {\rm V}) \ = $

3

Nun gelte $x_{\rm max} = 4\hspace{0.05cm} {\rm V}$. Wie groß ist die Wahrscheinlichkeit, dass $x$ zwischen $1\hspace{0.05cm} {\rm V}$ und $3\hspace{0.05cm} {\rm V}$ liegt?

$x_{\rm max} = 4\hspace{0.05cm} {\rm V}$:   ${\rm Pr}(1\hspace{0.05cm} {\rm V} < x <3\hspace{0.05cm} {\rm V}) \ =$

4

Wie groß ist die Wahrscheinlichkeit, dass $x$ genau gleich $2\hspace{0.05cm} {\rm V}$ ist?

$x_{\rm max} = 4\hspace{0.05cm} {\rm V}$:   ${\rm Pr}(x =2\hspace{0.05cm} {\rm V})\ =$

5

Es sei weiterhin $x_{\rm max} = 4\hspace{0.05cm} {\rm V}$. Welche der nachfolgenden Aussagen sind zutreffend?

	$y$ ist eine kontinuierliche Zufallsgröße.
	$y$ ist eine diskrete Zufallsgröße.
	$y$ ist eine gemischt kontinuierlich-diskrete Zufallsgröße.

6

Wie groß ist die Wahrscheinlichkeit, dass $y$ genau gleich $2\hspace{0.05cm} {\rm V}$ ist?

$x_{\rm max} = 4\hspace{0.05cm} {\rm V}$:   ${\rm Pr}(y =2\hspace{0.05cm} {\rm V})\ =$

Musterlösung

Musterlösung

(1)  Die Fläche unter der WDF muss stets den Wert $1$ ergeben. Daraus folgt: $${A}/{ 2}\cdot {4\hspace{0.5cm}V}=1\hspace{0.5cm}\Rightarrow\hspace{0.5cm} A \hspace{0.15cm}\underline{=\rm 0.5\;{1}/{V}}.$$

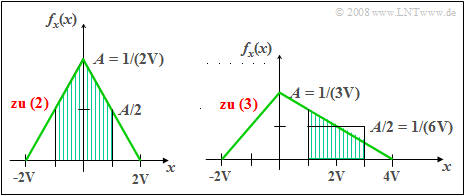
(2)  Mit $x_{\rm max} = 2\hspace{0.05cm} {\rm V}$ ergibt sich die WDF nach der linken Grafik. Die Schraffierung markiert die gesuchte Wahrscheinlichkeit und man erhält durch einfache geometrische Überlegungen: $${\rm Pr}(|x|<\rm 1\hspace{0.05cm} V)\hspace{0.15cm}\underline{=\rm 0.75}.$$

(3)  Mit $x_{\rm max} = 4\hspace{0.05cm} {\rm V}$ erhält man die rechts dargestellte WDF und den Maximalwert $A = 1/(3\hspace{0.05cm} {\rm V})$. Die schraffierte Fläche gibt wieder die gesuchte Wahrscheinlichkeit an, die man zum Beispiel über das flächengleiche Rechteck bestimmen kann: $${\rm Pr}(1\hspace{0.05cm} {\rm V}< x<3\hspace{0.05cm} {\rm V})=\rm \frac{1}{6\hspace{0.05cm} {\rm V}}\cdot 2\hspace{0.05cm} {\rm V}=\hspace{0.15cm}\underline{0.333}.$$

(4)  Diese Wahrscheinlichkeit ist definitionsgemäß gleich null ${\rm Pr}(x =2\hspace{0.05cm} {\rm V}) \;\underline {= 0}$, da $x$ eine kontinuierliche Zufallsgröße darstellt.

(5)  Nur die letzte Aussage der vorgegebenen Antworten ist zutreffend:

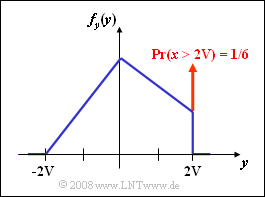
Die WDF $f_y(y)$ beinhaltet einen kontinuierlichen Anteil, aber auch eine Diracfunktion an der Stelle $y = 2\hspace{0.05cm} {\rm V}$ mit dem Gewicht ${\rm Pr}(x >2\hspace{0.05cm} {\rm V})$ .

(6)  Nebenstehend ist die Wahrscheinlichkeitsdichte der Zufallsgröße $y$ dargestellt. Aus der oberen rechten Abbildung zur Teilaufgabe (3) erkennt man den Zusammenhang: $${\rm Pr}( y=2\hspace{0.05cm} {\rm V})) = {\rm Pr}( x> 2\hspace{0.05cm} {\rm V})) = \frac{1}{2}\cdot\frac{1}{6\hspace{0.05cm} {\rm V}}\cdot2{\hspace{0.05cm} {\rm V}} = \hspace{-0.15cm}{1}/{6}\hspace{0.15cm}\underline{=0.167}.$$