Aufgabe 1.3: Entropienäherungen
Aus LNTwww
Version vom 24. November 2016, 16:23 Uhr von Markus (Diskussion | Beiträge)
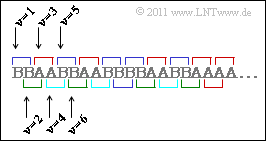
- Die Grafik zeigt vier Symbolfolgen 〈qν〉 mit jeweiliger Länge N = 60. Die Quellensymbole sind jeweils A und B. Daraus folgt direkt, dass für den Entscheidungsgehalt aller betrachteten Quellen H0 = 1 bit/Symbol gilt. Die Symbole A und B treten mit den Wahrscheinlichkeiten pA und pB auf.
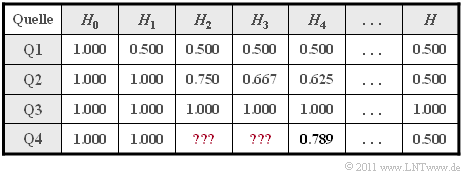
- Die folgende Tabelle zeigt neben H0 die Entropienäherungen
- H1, basierend auf pA und pB (Spalte 2),
- H2, basierend auf Zweiertupel (Spalte 3),
- H3, basierend auf Dreiertupel (Spalte 4),
- H4, basierend auf Vierertupel (Spalte 5),
- die tatsächliche Quellenentropie H, die sich aus Hk durch den Grenzübergang für k → ∞ ergibt (letzte Spalte).
- Zwischen diesen Entropien bestehen folgende Größenrelationen:
- $$H \le ... \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
- Nicht bekannt ist die Zuordnung zwischen den Quellen Q1, Q2, Q3, Q4 und den in der Grafik gezeigten gezeigten Symbolfolgen (Schwarz, Blau, Rot, Grün). Es ist lediglich bekannt, dass die Quelle Q4 einen Wiederholungscode beinhaltet. Zu bestimmen sind für diese Nachrichtenquelle schließlich noch die Entropienäherungen H2 und H3.
- Für die Quelle Q4 sind nur H1 = 1 bit/Symbol (⇒ A und B gleichwahrscheinlich), die Näherung H4 ≈ 0.789 bit/Symbol und der Entropie–Endwert H = 0.5 bit/Symbol angegeben. Letzterer aufgrund der Tatsache, dass bei der entsprechenden Symbolfolge jedes zweite Symbol keinerlei Information lierfert.
- Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 1.2. Für die k–te Entropienäherung gilt bei Binärquellen (M = 2) mit der Verbundwahrscheinlichkeit pi(k) eines k–Tupels:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{2^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_i^{(k)}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- 1. Es handelt sich um die Quelle Q3, da die Symbole gleichwahrscheinlich sind ⇒ H1 = H0 und keine statistischen Bindungen zwischen den Symbolen bestehen ⇒ H = .... = H2 = H1.
- 2. Man erkennt hier, dass A sehr viel häufiger auftritt als B, so dass H1 < H0 gelten muss. Entsprechend der Tabelle erfüllt nur die Quelle Q1 diese Bedingung. Aus H1 = 0.5 bit/Symbol kann man die Symbolwahrscheinlichkeiten pA≈ 0.89 und pB ≈ 0.11 ermitteln.
- 3. Durch Ausschlussverfahren kommt man zum Ergebnis Q2: Die Quelle Q1 gehört zur schwarzen Folge, Q3 zur blauen und Q4 zum Wiederholungscode und damit offensichtlich zur grünen Symbolfolge. Die rote Symbolfolge weist folgende Eigenschaften auf:
- Wegen H1 = H0 sind die Symbole gleichwahrscheinlich: pA = pB = 0.5.
- Wegen H < H1 bestehen statistische Bindungen innerhalb der Folge. Diese erkennt man daran, dass es mehr Übergänge zwischen A und B als bei statistischer Unabhängigkeit gibt.
- 4. Bei der grünen Symbolfolge (Quelle Q4) sind die Symbole A und B gleichwahrscheinlich:
- $$p_{\rm A} = p_{\rm B} = 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_1 = 1\,{\rm bit/Symbol} \hspace{0.05cm}.$$
- Zur Berechnung von H2 müssen Zweiertupel betrachtet und daraus die Verbundwahrscheinlichkeiten pAA, pAB, pBA und pBB berechnet werden. Aus der Skizze erkennt man:
- Die Kombinationen AB und BA sind nur dann möglich, wenn ein Tupel bei geradzahligem ν beginnt. Für die Verbundwahrscheinlichkeiten pAB und pBA gilt dann:
- $$p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}(\nu {\rm \hspace{0.15cm}ist\hspace{0.15cm}gerade}) \cdot {\rm Pr}( q_{\nu} = \mathbf{A}) \cdot {\rm Pr}(q_{\nu+1} = \mathbf{B}\hspace{0.05cm} | q_{\nu} = \mathbf{A}) = \\ \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{8} = p_{\rm BA} \hspace{0.05cm}.$$
- Dagegen gelten für die beiden weiteren Kombinationen AA und BB:
- $$p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}(\nu {\rm \hspace{0.15cm}ist\hspace{0.15cm}ungerade,\hspace{0.15cm}zum\hspace{0.15cm}Beispiel\hspace{0.15cm}1}) \cdot {\rm Pr}( q_1 = \mathbf{A}) \cdot {\rm Pr}(q_{2} = \mathbf{A}\hspace{0.05cm} | q_{1} = \mathbf{A}) + \\ \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(\nu {\rm \hspace{0.15cm}ist\hspace{0.15cm}gerade,\hspace{0.15cm}zum\hspace{0.15cm}Beispiel\hspace{0.15cm}2}) \cdot {\rm Pr}( q_{2} = \mathbf{A}) \cdot {\rm Pr}(q_{3} = \mathbf{A}\hspace{0.05cm} | q_{2} = \mathbf{A}) = \\ \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{2} \cdot \frac{1}{2} \cdot 1+ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{8} = p_{\rm BB} \hspace{0.05cm}.$$
- Damit ergibt sich für die Entropienäherung:
- $$H_2 \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{2} \cdot \left [ 2 \cdot \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}\frac {8}{3} + 2 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] =\\ = \hspace{0.1cm} \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) - \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(3) + \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) =\\ \hspace{0.1cm} = \hspace{0.1cm} 1.5 -0.375 \cdot 1.585 \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
- 5. Nach ähnlichem Vorgehen kommt man bei Dreiertupeln zu den Verbundwahrscheinlichkeiten
- $$p_{\rm AAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBB} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm ABA} = p_{\rm BAB} = 0 \hspace{0.05cm},\\ p_{\rm AAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABB} = p_{\rm BBA} = p_{\rm BAA} = 1/8$$
- und daraus zur Entropienäherung
- $$H_3 = \frac{1}{3} \cdot \left [ 2 \cdot \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm}(4) + 4 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{2.5}{3} \hspace{0.15cm} \underline {= 0.833 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
- Zur Berechnung von H4 ergeben sich folgende 16 Wahrscheinlichkeiten:
- $$p_{\rm AAAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBBB} = 3/16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm AABB} = p_{\rm BBAA} = 2/16 \hspace{0.05cm},\\ p_{\rm AAAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABBA} = p_{\rm ABBB} = p_{\rm BBBA} = p_{\rm BAAB} = p_{\rm BAAA}= 1/16 \hspace{0.05cm},\\ p_{\rm AABA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABAA} = p_{\rm ABAB} = p_{\rm BBAB} = p_{\rm BABB} = p_{\rm BABA}= 0\hspace{0.05cm}.$$
- Daraus folgt:
- $$H_4 \hspace{0.2cm} = \hspace{0.2cm} \frac{1}{4} \cdot \left [ 2 \cdot \frac{3}{16} \cdot {\rm log}_2\hspace{0.1cm}\frac{16}{3} + 2 \cdot \frac{1}{8} \cdot{\rm log}_2\hspace{0.1cm}(8) + 6 \cdot \frac{1}{16} \cdot {\rm log}_2\hspace{0.1cm}(16)\right ] =\\ \hspace{0.1cm} = \hspace{0.2cm} \left [ 6 \cdot {\rm log}_2\hspace{0.01cm}(16) - 6 \cdot {\rm log}_2\hspace{0.01cm}(3) + 4 \cdot {\rm log}_2\hspace{0.01cm}(8) + 6 \cdot {\rm log}_2\hspace{0.01cm}(16)\right ]/32 {= 0.789 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
- Man erkennt, dass auch die Näherung H4 = 0.789 bit/Symbol noch weit vom tatsächlichen Entropiewert H = 0.5 bit/Symbol abweicht.
- Hinweis: Der Wiederholungscode kann offensichtlich nicht durch eine Markovquelle modelliert werden. Wäre Q4 eine Markovquelle, so müsste nämlich gelten:
- $$H = 2 \cdot H_2 - H_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_2 = 1/2 \cdot (H+H_1) = 1/2 \cdot (0.5+1) = 0.75 \,{\rm bit/Symbol}\hspace{0.05cm}.$$