Aufgabe 3.7: PN–Modulation
Aus LNTwww
Version vom 17. August 2020, 13:02 Uhr von Guenter (Diskussion | Beiträge)
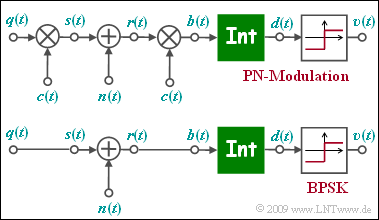
Die obere Grafik zeigt das Ersatzschaltbild der PN–Modulation $($englisch: Direct Sequence Spread Spectrum, abgekürzt $\rm DS–SS)$ im äquivalenten Tiefpass–Bereich, wobei $n(t)$ für AWGN–Rauschen steht.
Darunter skizziert ist das Tiefpass–Modell der binären Phasenmodulation, kurz $\rm BPSK$.
- Das Tiefpass–Sendesignal $s(t)$ ist hier nur aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal $q(t) ∈ \{+1, –1\}$ mit Rechteckdauer $T$ gesetzt.
- Die Funktion des Integrators kann wie folgt geschrieben werden:
- $$d (\nu T) = \frac{1}{T} \cdot \int_{(\nu -1 )T }^{\nu T} \hspace{-0.03cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$
- Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem $±1$–Spreizsignal $c(t)$ bei Sender und Empfänger, wobei von diesem Signal $c(t)$ lediglich der Spreizgrad $J$ bekannt ist.
- Für die Lösung dieser Aufgabe ist die Angabe der spezifischen Spreizfolge $($M–Sequenz oder Walsh–Funktion$)$ nicht von Bedeutung.
Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
auch für die PN–Modulation gültig ist, beziehungsweise wie die angegebene Gleichung zu modifizieren wäre.
Hinweise:
- Die Aufgabe gehört zum Kapitel Die Charakteristika von UMTS.
- Das bei UMTS eingesetzte CDMA–Verfahren firmiert auch unter der Bezeichnung „PN–Modulation”.
- Die in dieser Aufgabe verwendete Nomenklatur richtet sich zum Teil auch nach dem Abschnitt PN–Modulation im Buch „Modulationsverfahren”.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 3:
- Es handelt sich hier um einen optimalen Empfänger.
- Ohne Rauschen ist das Signal $b(t)$ innerhalb eines jeden Bits konstant gleich $+1$ oder $-1$.
- Aus der angegebenen Gleichung für den Integrator
- $$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.03cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t$$
- folgt, dass $d(\nu T)$ nur die Werte $±1$ annehmen kann.
(2) Richtig ist wieder der Lösungsvorschlag 3:
- Im rauschfreien Fall ⇒ $n(t) = 0$ kann auf die zweifache Multiplikation mit $c(t) ∈ \{+1, -1\}$ ⇒ $c(t)^{2} = 1$ verzichtet werden, so dass das obere Modell mit dem unteren Modell identisch ist.
(3) Zutreffend ist der Lösungsvorschlag 1:
- Da beide Modelle im rauschfreien Fall identisch sind, muss nur das Rauschsignal angepasst werden: $n'(t) = n(t) \cdot c(t)$.
- Die Lösungsvorschläge 2 und 3 sind dagegen nicht zutreffend: Die Integration muss auch weiterhin über $T = J \cdot T_{c}$ erfolgen $($nicht über $J \cdot T)$ und die PN–Modulation verringert das AWGN–Rauschen nicht.
(4) Richtig ist der Lösungsvorschlag 3:
- Die für BPSK und AWGN–Kanal gültige Gleichung
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$
- ist somit auch bei der PN–Modulation anwendbar und zwar unabhängig vom Spreizfaktor $J$ und von der spezifischen Spreizfolge.
- Bei AWGN–Rauschen wird die Fehlerwahrscheinlichkeit durch Bandspreizung weder vergrößert noch verkleinert.