Aufgabe 4.5: Nichtlineare Quantisierung

PCM-System mit Kompandierung

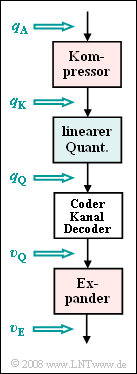
Zur Untersuchung der "nichtlinearen Quantisierung" gehen wir vom skizzierten Systemmodell aus.

Den Einfluss des Kanals und der PCM–Codierung bzw. –Decodierung lassen wir außer Acht.
Somit gilt stets $v_{\rm Q}(ν · T_{\rm A}) = q_{\rm Q}(ν · T_{\rm A})$, wobei im Weiteren auf die Zeitangabe $ν · T_{\rm A}$ verzichtet wird.

Durch den Vergleich von jeweils einer Ausgangsgröße mit einer Eingangsgröße kann man analysieren: Den Einfluss

des Kompressors ⇒ $q_{\rm K}(q_{\rm A})$,
des linearen Quantisierers ⇒ $q_{\rm Q}(q_{\rm K})$,
des nichtlinearen Quantisierers ⇒ $q_{\rm Q}(q_{\rm A})$,
des Expanders ⇒ $v_{\rm E}(v_{\rm Q})$ sowie
des Gesamtsystems ⇒ $v_{\rm E}(q_{\rm A})$.

Dabei wird von folgenden Voraussetzungen ausgegangen:

Alle Abtastwerte $q_{\rm A}$ liegen im Wertebereich $±1$ vor.
Der (lineare) Quantisierer arbeitet mit $M = 256$ Quantisierungsstufen, die mit $μ = 0$ bis $μ = 255$ gekennzeichnet werden.
Zur Kompression wird die sogenannte "13–Segment–Kennlinie" verwendet.

Das bedeutet:

Im Bereich $|q_{\rm A}| ≤ 1/64$ gilt $q_{\rm K} = q_{\rm A}$.
Für $q_{\rm A} > 1/64$ ergeben sich mit $k = 1$, ... , $6$ folgende sechs weitere Bereiche der Kompressorkennlinie:
⇒ Bereich $k\hspace{0.3cm}{\rm (falls}\hspace{0.3cm} 2^{k-7}< q_{\rm A} \le 2^{k-6}) \hspace{0.05cm}$ ⇒ $q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + {k}/{8}.$
Weitere sechs Bereiche gibt es für die negativen $q_{\rm A}$–Werte mit $k = -1$, ... , $-6$, die punktsymmetrisch zum Ursprung liegen. Diese werden in dieser Aufgabe jedoch nicht weiter betrachtet.

Hinweise:

Die Aufgabe gehört zum Kapitel "Pulscodemodulation".
Bezug genommen wird insbesondere auf die Seite Kompression und Expandierung.

Fragebogen

$q_{\rm K} \ = \ $

$\mu \ = \ $

$q_{\rm Q} \ = \ $

$v_{\rm E} \ = \ $

	Die Kennlinie $q_{\rm Q}(q_{\rm A})$ approximiert die Kompressorkennlinie in Stufen.
	Die Kennlinie $q_{\rm Q}(q_{\rm A})$ approximiert die Winkelhalbierende in Stufen.
	Die Stufenbreite ist in allen Segmenten $($außer für $k = 0)$ gleich groß.
	Die Stufenhöhe ist in allen Segmenten $($außer für $k = 0)$ gleich groß.

	Die Kennlinie $v_{\rm E}(q_{\rm A})$ approximiert die Kompressorkennlinie in Stufen.
	Die Kennlinie $v_{\rm E}(q_{\rm A})$ approximiert die Winkelhalbierende in Stufen.
	Die Stufenbreite ist in allen Segmenten $($außer für $k = 0)$ gleich groß.
	Die Stufenhöhe ist in allen Segmenten $($außer für $k = 0)$ gleich groß.

Musterlösung

(1) Der Abtastwert $q_{\rm A} = 0.4$ gehört zum Segment $k = 5$, das den Bereich $1/4 < q_{\rm A} ≤ 1/2$ abdeckt. Aus der angegebenen Gleichung folgt daraus mit $k = 5$:

$$q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + {k}/{8}={1}/{2}\cdot 0.4 + {5}/{8} \hspace{0.15cm}\underline {= 0.825}\hspace{0.05cm}.$$

(2) Der Eingangswert des linearen Quantisierers ist nun $q_{\rm K} = 0.825$, so dass folgende Rechnung zutrifft:

$${105}/{128} < q_{\rm K} = 0.825 \le {106}/{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 105 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 105\hspace{0.15cm}\underline { = 233} \hspace{0.05cm}.$$

(3) Gemäß der Angabenseite wird das Quantisierungsintervall $μ = 128 + m$ durch den Wert $q_{\rm Q} = 1/256 + m/128$ repräsentiert. Mit $m = 105$ folgt daraus:

$$q_{\rm Q} = \frac{1}{256} + \frac{105}{128} \hspace{0.15cm}\underline {\approx 0.824} \hspace{0.05cm}.$$

(4) Entsprechend der Musterlösung zur Teilaufgabe (3) gilt mit dem Eingangswert $q_{\rm A} = 0.04$:

$$ \frac{1}{32} < q_{\rm A} \le \frac{1}{16}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} k = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} q_{\rm K} = 2^2 \cdot 0.04 + \frac{2}{8}= 0.41$$

$$\Rightarrow \hspace{0.3cm}\frac{52}{128} < q_{\rm K} = 0.41 \le \frac{53}{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 52 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 52 = 180\hspace{0.3cm} \Rightarrow \hspace{0.3cm}q_{\rm Q} = \frac{1}{256} + \frac{52}{128} \hspace{0.15cm}\underline {= 0.41} \hspace{0.05cm}.$$

Kennlinien von Kompressor (blau) und Expander (grün)

(5) Wir suchen die Lösung in mehreren Schritten:

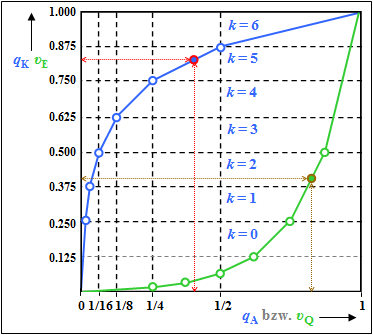
Beim Kompressor hat $q_{\rm A} = 0.4$ zum Ausgangswert $q_{\rm K} = 0.825$ geführt und nach der Quantisierung zum Wert $q_{\rm Q} = 0.824$ – siehe Teilaufgaben (1) und (3). Beachten Sie die roten Markierungen in der Grafik.
Die Grafik zeigt, dass sich damit empfängerseitig aus $v_{\rm Q} = 0.824$ näherungsweise wieder der Wert $v_{\rm E} ≈ 0.4$ ergibt ⇒ braune Markierungen in der Grafik.

Aufgrund der Quantisierung ist dies jedoch nur eine Näherung. Exakt gilt:

$$ v_{\rm E} = 0.25 + \frac{0.824-0.750}{0.875-0.750} \cdot 0.25 \hspace{0.15cm}\underline {= 0.398} \hspace{0.05cm}.$$

Dieser Rechengang ist anhand der Grafik nachvollziehbar. Obwohl die Expanderkennlinie $v_E(υ_{\rm Q})$ gleich der Umkehrfunktion der Kompressorkennlinie $q_K(q_{\rm A})$ ist, ergibt sich ein Fehler, da die Eingangsgröße $v_{\rm Q}$ des Expanders wertdiskret ist (Einfluss der Quantisierung).

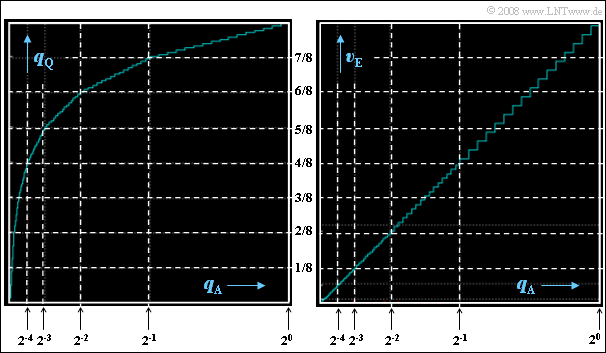
(6) Richtig sind die Aussagen 1 und 4, wie anhand der folgenden linken Grafik nachgeprüft werden kann:

13–Segment–Kennlinien: links: $q_{\rm Q}(q_{\rm A})$, rechts: $v_{\rm E}(q_{\rm A})$

Die Breite der einzelnen Stufen ist in jedem Segment unterschiedlich.
Im äußersten Segment $(k = 6)$ beträgt die Stufenbreite $0.5/16 = 1/32$, im nächsten Segment $(k = 5)$ nur mehr $0.25/16 = 1/64$.
Die Stufenbreiten in den weiteren Segmenten sind $1/128 \ (k = 4)$, $1/256 \ (k = 3)$, $1/512\ (k = 2)$ und $1/1024 \ (k = 1)$.
Der innerste Bereich von $-1/64$ bis $+1/64$ wird in $64$ Stufen unterteilt, woraus sich die Stufenbreite $1/2048$ ergibt.
Die Stufenhöhe ist dagegen in den Segmenten $k ≠ 0$ konstant gleich $1/8$ geteilt durch $16 = 1/128$ und im mittleren Segment gleich $1/256$.

(7) Richtig ist hier nur die zweite Aussage:

Durch den Expander verläuft die Quantisierung nun entlang der Winkelhalbierenden.
In jedem Segment sind Stufenbreite und Stufenhöhe konstant.
Wie die rechte Grafik zeigt, sind aber im nächstinneren Segment die Breite und die Höhe nur mehr halb so groß.