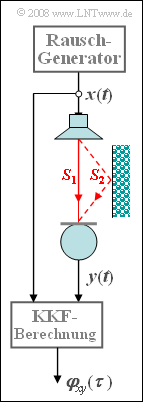
Aufgabe 4.14Z: Auffinden von Echos
Zur Messung akustischer Echos in Räumen – zum Beispiel bedingt durch Reflexionen an einer Wand – kann die nebenstehende Anordnung verwendet werden.
- Der Rauschgenerator erzeugt ein „im relevanten Frequenzbereich Weißes Rauschen” $x(t)$ mit Leistungsdichte $N_0 = 10^{-6} \hspace{0.08cm} \rm W/Hz$.
- Dieses ist bandbegrenzt auf $B_x = 20 \hspace{0.08cm} \rm kHz$ und wird auf einen Lautsprecher gegeben.
- Die gesamte Messeinrichtung ist für den Widerstandswert $R = 50 \hspace{0.08cm} \rm \Omega$ ausgelegt.
Das vom Mikrofon aufgenommene Signal ist im allgemeinsten Fall wie folgt beschreibbar:
- $$y(t) = \sum_{\mu = 1}^M \alpha_\mu \cdot x ( t - t_\mu ) .$$
Hierbei bezeichnen $\alpha_\mu$ Dämpfungsfaktoren und $t_\mu$ Laufzeiten.
Hinweise:
- Die Aufgabe gehört zum Kapitel Kreuzkorrelationsfunktion und Kreuzleistungsdichte.
- Benutzen Sie für numerische Berechnungen die Parameterwerte
- $$\alpha_1 = 0.5, \hspace{0.2cm}t_1 = 200 \,{\rm ms}, \hspace{0.2cm} \alpha_2 = 0.1, \hspace{0.2cm}t_2 = 250 \,{\rm ms}.$$
Fragebogen
Musterlösung
- $$\varphi_x (\tau) = {N_0}/{2} \cdot 2 B_x \cdot {\rm si} (2 \pi B_x \tau) = 0.02 \hspace {0.08cm}{\rm W} \cdot {\rm si} (2 \pi B_x \tau).$$
- Umgerechnet von $R = 50 \hspace{0.08cm} \rm \Omega$ auf $R = 1 \hspace{0.08cm} \rm \Omega$ erhält man somit (Multiplikation mit $R = 50 \hspace{0.08cm} \rm \Omega$):
- $$\varphi_x (\tau) = 0.02 \hspace {0.05cm}{\rm VA} \cdot 50 \hspace {0.05cm}{\rm V/A}\cdot {\rm si} (2 \pi B_x \tau)= 1 \hspace {0.05cm}{\rm V}^2 \cdot {\rm si} (2 \pi B_x \tau).$$
- Der Effektivwert ist die Wurzel aus dem AKF-Wert bei $\tau = 0$:
- $$\sigma_x \hspace{0.15cm}\underline{= 1 \hspace {0.08cm}{\rm V}}.$$
(2) Für die Kreuzkorrelationsfunktion (KKF) gilt im vorliegenden Fall:
- $$\varphi_{xy} (\tau) = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)} = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}\big [ \alpha_1 \cdot x(t- t_1+ \tau)\hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot x(t- t_2+ \tau)\big] } . $$
- Nach Aufspaltung der Mittelwertbildung auf die beiden Terme erhält man hieraus:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_1+ \tau)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_2+ \tau)} .$$
- Unter Verwendung der AKF $\varphi_x(\tau)$ kann hierfür auch geschrieben werden:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot {\varphi_{x}(\tau- t_1)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2\cdot {\varphi_{x}(\tau- t_2)} = 1 \hspace {0.08cm}{\rm V}^2 \cdot \left[ \alpha_1 \cdot {\rm si} (2 \pi B_x (\tau - t_1)) + \alpha_2 \cdot {\rm si} (2 \pi B_x (\tau - t_2)) \right].$$
- Die si-Funktion weist äquidistante Nulldurchgänge bei allen Vielfachen von $1/(2B_x) = 25 \hspace{0.08cm} µ s$ auf, jeweils bezogen auf deren Mittellagen bei $t_1 = 200 \hspace{0.08cm} {\rm ms}$ bzw. $t_2 = 250 \hspace{0.08cm} {\rm ms}$.
- Daraus ergeben sich die KKF-Werte zu:
- $$\varphi_{xy} (\tau = 0) \hspace{0.15cm}\underline{= 0},\hspace{0.5cm}\varphi_{xy} (\tau = t_1)= \alpha_1 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.5\,{\rm V}^2} ,\hspace{0.5cm} \varphi_{xy} (\tau = t_2)= \alpha_2 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.1\,{\rm V}^2} .$$
(3) Das Kreuzleistungsdichtespektrum (KLDS) ist die Fouriertransformierte der KKF, ebenso wie das Leistungsdichtespektrum (LDS) die Fouriertransformierte der AKF angibt. Für dieses gilt:
- $${\it \Phi}_{xy} (f) = \alpha_1 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_2}. $$
- Außerhalb des Bereichs $|f| \le B_x$ ist das LDS ${\it \Phi}_{x}(f)$ – und dementsprechend auch das KLDS ${\it \Phi}_{xy}(f)$ – identisch $0$.
- Innerhalb dieses Intervalls gilt dagegen ${\it \Phi}_{x}(f) = N_0/2$. Daraus folgt in diesem Bereich:
- $${\it \Phi}_{xy} (f) = {N_0}/{2} \left( \alpha_1 \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\rm e}^{-{\rm j}2 \pi f t_2} \right). $$
- Es ist ersichtlich, dass ${\it \Phi}_{xy}(f)$ im Gegensatz zu ${\it \Phi}_{x}(f)$ eine komplexe Funktion ist. Bei $f = 0$ gilt:
- $${\it \Phi}_{xy} (f = 0) = {N_0}/{2} \left( \alpha_1 \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \right) = 0.3 \cdot 10^{-6}\hspace{0.05cm}{\rm W/Hz} \hspace{0.15cm}\underline{= 15 \cdot 10^{-6}\hspace{0.07cm}{\rm V^2/Hz}} . $$
(4) Richtig sind die Lösungsvorschläge 1 und 3:
- Die Fouriertransformierte einer diracförmigen AKF führt zu einem für alle Frequenzen $f$ konstanten LDS, das heißt tatsächlich zu „ echt Weißem Rauschen”.
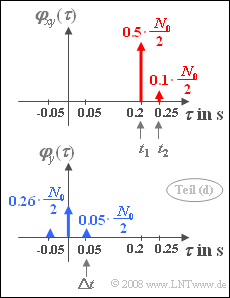
- Dieses besitzt eine unendlich große Leistung, und für die KKF kann dann entsprechend der oberen Grafik geschrieben werden:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot { N_0}/{2} \cdot {\rm \delta}( \tau - t_1) \hspace {0.1cm}+ \hspace {0.1cm} \alpha_2 \cdot { N_0}/{2} \cdot {\rm \delta}( \tau - t_2) .$$
- Im Frequenzbereich ist für $|f| \le B_x$ tatsächlich kein Unterschied gegenüber der Teilaufgabe (3) feststellbar.
- Da nun aber echt weißes Rauschen vorliegt, ist aber hier das KLDS nicht auf diesen Bereich beschränkt.
(5) Für die AKF des echobehafteten Signals gilt: $\varphi_{y} (\tau) = \overline {y(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)}$. Diese AKF $\varphi_{y} (\tau)$ lässt sich demzufolge als die folgende Summe darstellen:
- $$\alpha_1^2 \cdot \overline {x(t - t_1) \cdot x(t - t_1+ \tau)} \hspace{0.03cm} + \hspace{0.03cm} \alpha_1\hspace{0.02cm}\alpha_2 \cdot \overline {x(t - t_1) \cdot x(t - t_2+ \tau)} + \hspace{0.05cm} \alpha_2\hspace{0.02cm}\alpha_1 \cdot \overline {x(t - t_2) \cdot x(t - t_1+ \tau)}\hspace{0.03cm} + \hspace{0.03cm} \alpha_2^2 \cdot \overline {x(t - t_2) \cdot x(t - t_2+ \tau)}. $$
Für den ersten und den letzten Mittelwert gilt:
- $$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + \tau)} =\varphi_x(\tau).$$
Dagegen erhält man für den zweiten und den dritten Mittelwert mit $\Delta t = t_2 - t_1= 50 \ \rm ms$:
- $$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_1- t_2+ \tau)} =\varphi_x(\tau - \Delta t),$$
- $$\overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_2- t_1+ \tau)} =\varphi_x(\tau + \Delta t).$$
Insgesamt ergibt sich somit wieder eine symmetrische AKF, wie in der unteren Grafik dargestellt:
- $$\varphi_{y} (\tau) = {N_0}/{2} \cdot \left[ ( \alpha_1^2 \hspace{0.1cm} + \hspace{0.1cm} \alpha_2^2 ) \cdot {\rm \delta} (\tau) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau - \Delta t) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau + \Delta t) \right].$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{y} (\tau = 0 ) \hspace{0.15cm}\underline{= 0.13 \cdot 10^{-6}\, {\rm W/Hz}}, \hspace{0.3cm}\varphi_{y} (\tau = \Delta t )\hspace{0.15cm}\underline{ = 0.025 \cdot 10^{-6}\, {\rm W/Hz}}.$$