Leistungsdichtespektrum (LDS)
Inhaltsverzeichnis
Theorem von Wiener-Chintchine
Im Weiteren beschränken wir uns auf ergodische Prozesse. Wie im letzten Kapitel gezeigt wurde, gelten dann die folgenden Aussagen:
- Jede einzelne Musterfunktion $x_i(t)$ ist repräsentativ für den gesamten Zufallsprozess $\{x_i(t)\}$.
- Alle Zeitmittelwerte sind somit identisch mit den dazugehörigen Scharmittelwerten.
- Die Autokorrelationsfunktion, die allgemein von den beiden Zeitparametern $t_1$ und $t_2$ beeinflusst wird, hängt nur noch von der Zeitdifferenz $τ = t_2 – t_1$ ab:
- $$\varphi_x(t_1,t_2)={\rm E}[x(t_{\rm 1})\cdot x(t_{\rm 2})] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$
Die Autokorrelationsfunktion liefert quantitative Aussagen über die (linearen) statistischen Bindungen innerhalb des ergodischen Prozesses $\{x_i(t)\}$ im Zeitbereich. Die äquivalente Beschreibungsgröße im Frequenzbereich ist die spektrale Leistungsdichte, häufig auch als „Leistungsdichtespektrum” bezeichnet.
$\text{Definition:}$ Das Leistungsdichtespektrum (LDS) eines ergodischen Zufallsprozesses $\{x_i(t)\}$ ist die Fouriertransformierte der Autokorrelationsfunktion (AKF): $${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\pi} f \tau} {\rm d} \tau. $$ Diesen Funktionalzusammenhang nennt man das Theorem von Wiener und Chintchine.
Ebenso kann die AKF als Fourierrücktransformierte des LDS berechnet werden (siehe Seite Fourierrücktransformation im Buch „Signaldarstellung”):
- $$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{{\rm j\pi} f \tau} {\rm d} f.$$
- Die beiden Gleichungen sind nur dann direkt anwendbar, wenn der Zufallsprozess weder einen Gleichanteil noch periodische Anteile beinhaltet.
- Andernfalls muss man nach den Angaben entsprechend der Seite Spektrale Leistungsdichte mit Gleichsignalkomponente vorgehen.
Physikalische Interpretation und Messung
Das folgende Bild zeigt eine Anordnung zur (näherungsweisen) messtechnischen Bestimmung des Leistungsdichtespektrums ${\it \Phi}_x(f)$.
Hierzu ist folgendes anzumerken:
- Das Zufallssignal $x(t)$ wird auf ein (möglichst) rechteckförmiges und (möglichst) schmalbandiges Filter mit Mittenfrequenz $f$ und Bandbreite $Δf$ gegeben, wobei $Δf$ entsprechend der gewünschten Frequenzauflösung hinreichend klein gewählt werden muss.
- Das entsprechende Ausgangssignal $x_f(t)$ wird quadriert und anschließend der Mittelwert über eine hinreichend lange Messdauer $T_{\rm M}$ gebildet. Damit erhält man die Leistung von $x_f(t)$ bzw. die Leistungsanteile von $x(t)$ im Spektralbereich von $f - Δf/2$ bis $f + Δf/2$:
- $$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f(t)^2 \hspace{0.1cm}\rm d \it t.$$
- Die Division durch $Δf$ führt von der spektralen Leistung zur spektralen Leistungsdichte:
- $${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} {\rm bzw.} \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$
- Hierbei bezeichnet ${\it \Phi}_{x+}(f) = 2 · {\it \Phi}_x(f)$ das einseitige, nur für positive Frequenzen definierte LDS. Für negative Frequenzen ist ${\it \Phi}_{x+}(f) = 0$. Im Gegensatz dazu gilt für das üblicherweise verwendete zweiseitige LDS: ${\it \Phi}_x(–f) = {\it \Phi}_x(f)$.
- Während die Leistung $P_{x_f}$ mit kleiner werdender Bandbreite $Δf$ gegen Null tendiert, bleibt die spektrale Leistungsdichte ab einem hinreichend kleinen Wert von $Δf$ nahezu konstant. Für die exakte Bestimmung von ${\it \Phi}_x(f)$ sind zwei Grenzübergänge notwendig:
- $${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$
$\text{Fazit:}$ Aus dieser physikalischen Interpretation folgt weiter, dass das Leistungsdichtespektrum stets reell ist und nie negativ werden kann. Die gesamte Signalleistung von $x(t)$ erhält man dann durch Integration über alle Spektralanteile:
- $$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$
Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite
Alle im Buch „Signaldarstellung” für deterministische Signale hergeleiteten Gesetzmäßigkeiten der Fouriertransformation können auch auf die
Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) eines Zufallsprozesses angewendet werden. Aufgrund der spezifischen Eigenschaften
- von Autokorrelationsfunktion (stets reell und gerade) und
- Leistungsdichtespektrum (stets reell, gerade und nicht-negativ)
liefern allerdings nicht alle Gesetze sinnvolle Ergebnisse.
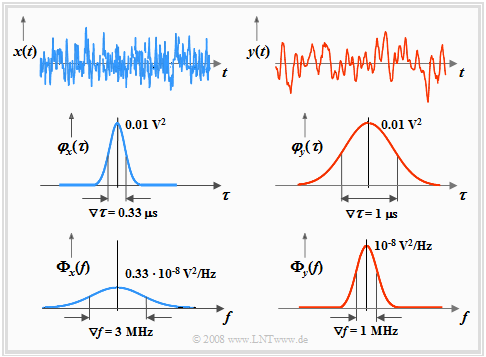
Wir betrachten nun wie im Abschnitt Interpretation der Autokorrelationsfunktion zwei unterschiedliche ergodische Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ anhand
- der beiden Mustersignale $x(t)$ bzw. $y(t)$ ⇒ obere Skizze,
- der beiden Autokorrelationsfunktionen $φ_x(τ)$ bzw. $φ_y(τ)$ ⇒ mittlere Skizze,
- der beiden Leistungsdichtespektren ${\it \Phi}_x(f)$ bzw. ${\it \Phi}_y(f)$ ⇒ untere Skizze.
Anhand dieser Grafiken sind folgende Aussagen möglich:
- Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ besitzen gleiche Leistung:
- $${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$
- Das aus der klassischen (deterministischen) Systemtheorie bekannte Reziprozitätsgesetz von Zeitdauer und Bandbreite gilt hier ebenfalls: Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt.
- Als Beschreibungsgröße verwenden wir hier die äquivalente LDS-Bandbreite $∇f$ (man spricht Nabla-f), ähnlich definiert wie die äquivalente AKF-Dauer $∇τ$ im Kapitel Interpretation der Autokorrelationsfunktion:
- $${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$
- Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang:
- $${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$
$\text{Beispiel 1:}$ Wir gehen von der obigen Grafik aus:
- Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ und $∇f_x = 3 \hspace{0.08cm} \rm MHz$.
- Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y = 1 \hspace{0.08cm} \rm µs$.
- Die äquivalente LDS-Bandbreite beträgt somit nur mehr $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$.
$\text{Allgemein gilt:}$ Das Produkt aus äquivalenter AKF-Dauer ${ {\rm \nabla} \tau_x}$ und äquivalenter LDS-Bandbreite $ { {\rm \nabla} f_x}$ ist gleich $1$:
- $${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$
$\text{Beweis:}$ Entsprechend den obigen Definitionen gilt:
- $${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it \Phi}_x(f = {\rm 0)} }{ \varphi_x(\tau = \rm 0)},$$
- $${ {\rm \nabla} f_x} = \frac {1}{ {\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{ {\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)} }{ {\it \Phi}_x(f = \rm 0)}.$$
Das Produkt ist somit gleich $1$:
$\text{Beispiel 2:}$ Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte Weiße Rauschen dar:
- Dieses beinhaltet alle Spektralanteile (bis ins Unendliche).
- Die äquivalente LDS-Bandbreite $∇f$ ist unendlich groß.
Das hier angegebene Gesetz besagt, dass damit für die äquivalente AKF-Dauer $∇τ = 0$ gelten muss ⇒ das weiße Rauschen besitzt eine diracförmige AKF.
Mehr zu dieser Thematik finden Sie im dreiteiligen Lernvideo Der AWGN-Kanal, insbesondere im zweiten Teil.
Leistungsdichtespektrum mit Gleichsignalkomponente
Wir gehen zunächst von einem gleichsignalfreien Zufallsprozess $\{x_i(t)\}$ aus. Weiterhin setzen wir voraus, dass der Prozess auch keine periodischen Anteile beinhaltet.
Dann gilt:
- Die Autokorrelationsfunktion $φ_x(τ)$ verschwindet für $τ → ∞$.
- Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ – berechenbar als die Fouriertransformierte von $φ_x(τ)$ – ist sowohl wert– als auch zeitkontinuierlich, also ohne diskrete Anteile.
Wir betrachten nun einen zweiten Zufallsprozess $\{y_i(t)\}$, der sich vom Prozess $\{x_i(t)\}$ lediglich durch eine zusätzliche Gleichsignalkomponente $m_y$ unterscheidet:
- $$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$
Die statistischen Beschreibungsgrößen des mittelwertbehafteten Zufallsprozesses $\{y_i(t)\}$ weisen dann folgende Eigenschaften auf:
- Der Grenzwert der AKF für $τ → ∞$ ist nun nicht mehr Null, sondern $m_y^2$. Im gesamten $τ$-Bereich von $–∞$ bis $+∞$ ist die AKF $φ_y(τ)$ um $m_y^2$ größer als $φ_x(τ)$:
- $${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$
- Nach den elementaren Gesetzen der Fouriertransformation führt der konstante AKF-Beitrag im LDS zu einer Diracfunktion $δ(f)$ mit dem Gewicht $m_y^2$:
- $${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$
- Nähere Informationen zur Diracfunktion finden Sie im Kapitel Gleichsignal - Grenzfall eines periodischen Signals des Buches „Signaldarstellung”.
- Weiterhin möchten wir Sie auf das Lernvideo Herleitung und Visualisierung der Diracfunktion hinweisen.
Numerische LDS-Ermittlung
Autokorrelationsfunktion und Leistungsdichtespektrum sind über die Fouriertransformation streng miteinander verknüpft. Dieser Zusammenhang gilt auch bei zeitdiskreter AKF-Darstellung mit dem Abtastoperator ${\rm A} \{ \varphi_x ( \tau ) \} $, also für
- $${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$
Der Übergang vom Zeit– in den Spektralbereich kann mit folgenden Schritten hergeleitet werden:
- Der Abstand $T_{\rm A}$ zweier Abtastwerte ist durch die absolute Bandbreite $B_x$ (maximal auftretende Frequenz innerhalb des Prozesses) über das Abtasttheorem festgelegt:
- $$T_{\rm A}\le\frac{1}{2B_x}.$$
- Die Fouriertransformierte der zeitdiskreten (abgetasteten) AKF ergibt ein mit ${\rm 1}/T_{\rm A}$ periodisches LDS:
- $${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$
$\text{Fazit:}$ Da sowohl $φ_x(τ)$ als auch ${\it \Phi}_x(f)$ gerade und reelle Funktionen sind, gilt der Zusammenhang:
- $${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} k T_{\rm A}).$$
- Das Leistungsdichtespektrum (LDS) des zeitkontinuierlichen Prozesses erhält man aus ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ durch Bandbegrenzung auf den Frequenzbereich $\vert f \vert ≤ 1/(2T_{\rm A})$.
- Im Zeitbereich bedeutet diese Operation eine Interpolation der einzelnen AKF-Abtastwerte mit der ${\rm si}$–Funktion, wobei ${\rm si}(x)$ für $\sin(x)/x$ steht.
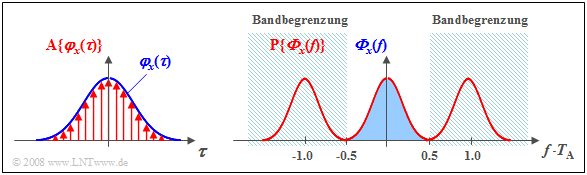
$\text{Beispiel 3:}$ Eine gaußförmige AKF $φ_x(τ)$ wird im Abstand $T_{\rm A}$ abgetastet, wobei das Abtasttheorem erfüllt ist:
- Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{φ_x(τ) \}$ sei ${\rm P} \{ { {\it \Phi}_x} ( f) \}$. Diese mit ${\rm 1}/T_{\rm A}$ periodische Funktion ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ ist dementsprechend unendlich weit ausgedehnt ( roter Kurvenzug ).
- Das LDS ${\it \Phi}_x(f)$ des zeitkontinuierlichen Prozesses $\{x_i(t)\}$ erhält man durch Bandbegrenzung auf den im Bild blau hinterlegten Frequenzbereich $\vert f · T_{\rm A} \vert ≤ 0.5$.
Genauigkeit der numerischen LDS-Berechnung
Für die nachfolgende Analyse gehen wir von folgenden Annahmen aus:
- Die zeitdiskrete AKF $φ_x(k · T_{\rm A})$ wurde aus $N$ Abtastwerten numerisch ermittelt. Wie bereits auf der Seite Genauigkeit der numerischen AKF-Berechnung gezeigt wurde, sind diese Werte fehlerhaft und die Fehler korreliert, wenn $N$ zu klein gewählt wurde.
- Zur Berechnung des periodischen Leistungsdichtespektrums (LDS) verwenden wir nur die AKF-Werte $φ_x(0)$, ... , $φ_x(K · T_{\rm A})$:
- $${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} k T_{\rm A}).$$
$\text{Fazit:}$ Die Genauigkeit der LDS-Berechnung wird im starken Maße durch den Parameter $K$ bestimmt:
- Ist $K$ zu klein gewählt, so werden die eigrntlich vorhandenen AKF-Werte $φ_x(k · T_{\rm A})$ mit $k > K$ nicht berücksichtigt.
- Bei zu großem $K$ werden auch solche AKF-Werte berücksichtigt, die eigentlich Null sein sollten und nur wegen der numerischen AKF-Berechnung endlich sind.
- Diese Werte sind allerdings – bedingt durch ein zu kleines $N$ bei der AKF–Ermittlung – nur Fehler, und beinträchtigen die LDS-Berechnung mehr als dass sie einen brauchbaren Beitrag zum Ergebnis liefern.
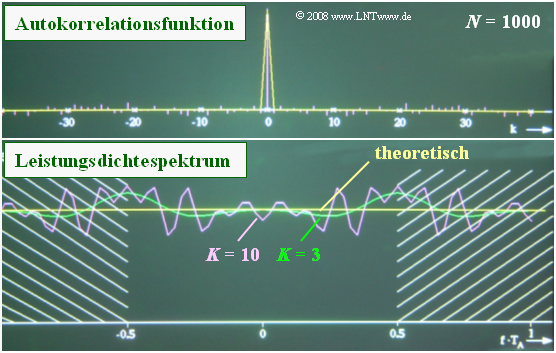
$\text{Beispiel 4:}$ Wir betrachten hier einen mittelwertfreien Prozess mit statistisch unabhängigen Abtastwerten.
- Deshalb sollte nur der AKF–Wert $φ_x(0) = σ_x^2$ von $0$ verschieden ist.
- Ermittelt man aber die AKF numerisch aus lediglich $N = 1000$ Abtastwerten, so erhält man auch für $k ≠ 0$ endliche AKF–Werte.
- Das obere Bild zeigt, dass diese fehlerhaften AKF–Werte bis zu $6\%$ des Maximalwertes betragen können.
- Unten ist das numerisch ermittelte LDS dargestellt. Gelb ist der theoretische Verlauf dargestellt, der für $\vert f · T_{\rm A} \vert ≤ 0.5$ konstant sein sollte.
- Die grüne und die violette Kurve verdeutlichen, wie durch $K = 3$ bzw. $K = 10$ das Ergebnis gegenüber $K = 0$ verfälscht wird.
In diesem Fall (statistisch unabhängige Zufallsgrößen) wächst der Fehler monoton mit steigendem $K$. Bei einer Zufallsgröße mit statistischen Bindungen gibt es dagegen jeweils einen optimalen Wert für $K$.
- Wird dieser zu klein gewählt, so werden signifikante Bindungen nicht berücksichtigt.
- Ein zu großer Wert führt dagegen zu Oszillationen, die nur auf fehlerhafte AKF–Werte zurückzuführen sind.
Aufgaben zum Kapitel
Aufgabe 4.12: LDS eines Binärsignals
Aufgabe 4.12Z: Weißes Rauschen