Aufgabe 3.1: cos² - und Dirac-WDF
Aus LNTwww
Version vom 7. März 2017, 15:30 Uhr von Guenter (Diskussion | Beiträge)
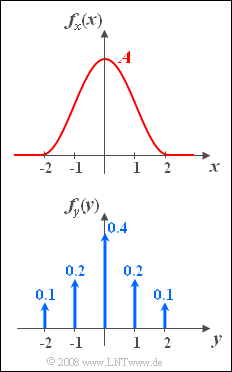
Die Grafik zeigt die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier Zufallsgrößen $x$ und $y$.
- Die WDF der Zufallsgröße $x$ lautet in analytischer Form:
- $$f_x(x)=\left\{\begin{array}{*{4}{c}}A\rm \cdot \rm cos^2(\frac{\pi}{4}\cdot \it x) &\rm f\ddot{u}r\hspace{0.1cm} -2\le \it x\le \rm 2, \\0 & \rm sonst. \\\end{array}\right.$$
- Dagegen besteht die WDF der Zufallsgröße $y$ aus insgesamt fünf Diracfunktionen mit den in der unteren Grafik angegebenen Gewichten.
Betrachtet man diese Zufallsgrößen als Momentanwerte zweier Zufallssignale $x(t)$ und $y(t)$), so ist offensichtlich, dass beide Signale auf den Bereich $\pm 2$ „amplitudenbegrenzt“ sind. Betragsmäßig größere Werte kommen nicht vor.
Hinweise:
- Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichtefunktion.
- Bezug genommen wird aber auch auf das Kapitel Vom Zufallsexperiment zur Zufallsgröße.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Es gilt folgende Gleichung:
- $$\int \rm cos^{\rm 2}(\it ax)\, {\rm d}x=\frac{\it x}{\rm 2}+\frac{\rm 1}{\rm 4 \it a}\cdot \rm sin(\rm 2\it ax).$$
Fragebogen
Musterlösung
- 1. Richtig sind die Aussagen 1, 2 und 4: x ist wertkontinuierlich und y wertdiskret (M = 5). Die WDF liefert keine Aussagen darüber, ob eine Zufallsgröße zeitdiskret oder zeitkontinuierlich ist.
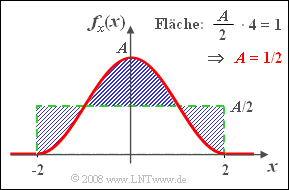
- 2. Die Fläche unter der WDF muss 1 ergeben. Durch einfache geometrische Überlegungen kommt man zum Ergebnis A = 0.5.
- 3. Die Wahrscheinlichkeit, dass die wertkontinuierliche Zufallsgröße x einen festen Wert x0 annimmt, ist stets vernachlässigbar klein ⇒ Pr(x = 0) = 0. Für die wertdiskrete Zufallsgröße y gilt dagegen gemäß der Angabe: Pr(y = 0) = 0.4 (Gewicht der Diracfunktion bei y = 0).
- 4. Wegen Pr(x = 0) und der WDF-Symmetrie ergibt sich Pr(x > 0) = 0.5.
- 5. Da y eine diskrete Zufallsgröße ist, addieren sich die Wahrscheinlichkeiten für y = 1 und y = 2:
- $$\rm Pr(\it y >\rm 0) = \rm Pr(\it y = \rm 1) + \rm Pr(\it y = \rm 2) \hspace{0.15cm}\underline {= 0.3}.$$
- 6. Das Ereignis „| y | < 1” ist hier identisch mit „y = 0”. Damit erhält man:
- $$\rm Pr(|\it y| < \rm 1) = \rm Pr(\it y = \rm 0)\hspace{0.15cm}\underline { = 0.4}.$$
- 7. Die gesuchte Wahrscheinlichkeit ist gleich dem Integral von -1 bis +1 über die WDF der kontinuierlichen Zufallsgröße x. Unter Berücksichtigung der Symmetrie und der angegebenen Gleichung erhält man:
- $$\rm Pr(|\it x|<\rm 1)=\rm 2 \cdot \int_{0}^{1}\frac{1}{2}\cdot cos^2(\frac{\pi}{4}\cdot \it x)\hspace{0.1cm}{\rm d}x=\frac{x}{\rm 2}+\frac{\rm 1}{\pi}\cdot\rm sin(\frac{\pi}{2}\cdot\it x)\Bigg |_{\rm 0}^{\rm 1}=\rm\frac{1}{2} + \frac{1}{\pi} \hspace{0.15cm}\underline{ \approx 0.818}.$$