Aufgaben:Aufgabe 5.5Z: Zum RAKE–Empfänger: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Fehlerwahrscheinlichkeit der PN–Modulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Mul…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1888__Mod_Z_5_5.png|right|]] |
| + | Die Grafik zeigt einen Zweiwegekanal (gelbe Hinterlegung). Die entsprechende Beschreibungsgleichung lautet: | ||
| + | $$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$ | ||
| + | Die Verzögerung auf dem Nebenpfad sei $τ = 1 μs$. Darunter gezeichnet ist die Struktur eines RAKE–Empfängers (grüne Hinterlegung) mit den allgemeinen Koeffizienten $K, h_0, h_1, τ_0$ und $τ_1$. | ||
| + | |||
| + | Der RAKE–Empfänger hat die Aufgabe, die Energie der beiden Signalpfade zu bündeln und dadurch die Entscheidung sicherer zu machen. Die gemeinsame Impulsantwort von Kanal und RAKE–Empfänger kann in der Form | ||
| + | $$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$ | ||
| + | angegeben werden, allerdings nur dann, wenn die RAKE–Koeffizienten $h_0$, $h_1$, $τ_0$ und $τ_1$ geeignet gewählt werden. Der Hauptanteil von $h_{KR}(t)$ soll bei $t = τ$ liegen. | ||
| + | |||
| + | Die Konstante K ist so zu wählen, dass die Amplitude des Hauptpfads $A_1 = 1$ ist: | ||
| + | $$K= \frac{1}{h_0^2 + h_1^2}.$$ | ||
| + | Gesucht sind außer den geeigneten RAKE–Parametern auch die Signale $r(t)$ und $b(t)$, wenn $s(t)$ ein Rechteck der Höhe 1 und der Breite $T = 5 μs$ ist. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf der [http://www.lntwww.de/Modulationsverfahren/Fehlerwahrscheinlichkeit_der_PN%E2%80%93Modulation#Untersuchungen_zum_RAKE.E2.80.93Empf.C3.A4nger_.282.29 Untersuchungen zum RAKE–Empfänger] von [http://www.lntwww.de/Modulationsverfahren/Fehlerwahrscheinlichkeit_der_PN%E2%80%93Modulation Kapitel 5.4]. | ||
| + | |||
Version vom 7. Januar 2017, 18:16 Uhr
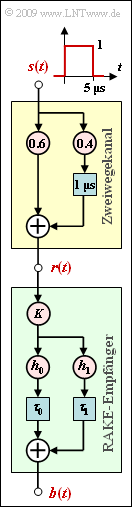
Die Grafik zeigt einen Zweiwegekanal (gelbe Hinterlegung). Die entsprechende Beschreibungsgleichung lautet: $$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$ Die Verzögerung auf dem Nebenpfad sei $τ = 1 μs$. Darunter gezeichnet ist die Struktur eines RAKE–Empfängers (grüne Hinterlegung) mit den allgemeinen Koeffizienten $K, h_0, h_1, τ_0$ und $τ_1$.
Der RAKE–Empfänger hat die Aufgabe, die Energie der beiden Signalpfade zu bündeln und dadurch die Entscheidung sicherer zu machen. Die gemeinsame Impulsantwort von Kanal und RAKE–Empfänger kann in der Form $$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$ angegeben werden, allerdings nur dann, wenn die RAKE–Koeffizienten $h_0$, $h_1$, $τ_0$ und $τ_1$ geeignet gewählt werden. Der Hauptanteil von $h_{KR}(t)$ soll bei $t = τ$ liegen.
Die Konstante K ist so zu wählen, dass die Amplitude des Hauptpfads $A_1 = 1$ ist: $$K= \frac{1}{h_0^2 + h_1^2}.$$ Gesucht sind außer den geeigneten RAKE–Parametern auch die Signale $r(t)$ und $b(t)$, wenn $s(t)$ ein Rechteck der Höhe 1 und der Breite $T = 5 μs$ ist.
Hinweis: Die Aufgabe bezieht sich auf der Untersuchungen zum RAKE–Empfänger von Kapitel 5.4.
Fragebogen
Musterlösung