Digitalsignalübertragung/Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 136: | Zeile 136: | ||
*NRZ–Rechtecke mit Amplitude <i>s</i><sub>0</sub>, AWGN–Rauschen mit <i>N</i><sub>0</sub>, wobei | *NRZ–Rechtecke mit Amplitude <i>s</i><sub>0</sub>, AWGN–Rauschen mit <i>N</i><sub>0</sub>, wobei | ||
| − | ::<math></math> | + | ::<math>10 \cdot {\rm lg}\hspace{0.1cm} \frac{s_0^2 \cdot T}{N_0}\approx |
| − | + | 13\,{\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | |
| + | \frac{N_0}{s_0^2 \cdot T} = 0.05\hspace{0.05cm}.</math> | ||
| − | * | + | *Gaußförmiges Empfangsfilter mit Grenzfrequenz <i>f</i><sub>G</sub> · <i>T</i> = 0.4: |
| + | ::<math>\sigma_d^2 = \frac{(N_0 /T)\cdot (f_{\rm G}\cdot T)}{\sqrt{2}}= \frac{0.05 \cdot | ||
| + | s_0^2\cdot0.4}{\sqrt{2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_d = \sqrt{0.0141}\cdot s_0 | ||
| + | \approx 0.119 \cdot s_0 \hspace{0.05cm}.</math> | ||
| + | *Für die Detektionsgrundimpulswerte gilt: | ||
| + | ::<math>g_0 = g_d(t=0) \approx 0.68 \cdot s_0,</math> | ||
| + | ::<math> g_1 = g_d(t=T) \approx 0.16 \cdot s_0, \hspace{0.2cm} g_{-1} = g_d(t=-T) \approx | ||
| + | 0.16 \cdot s_0\hspace{0.05cm}.</math> | ||
| + | |||
| + | Alle anderen Grundimpulswerte können vernachlässigt werden.<br> | ||
| + | |||
| + | [[Datei:P ID1377 Dig T 3 2 S3 version1.png|Augendiagramm und WDF des Nutzsignals|class=fit]]<br> | ||
| + | |||
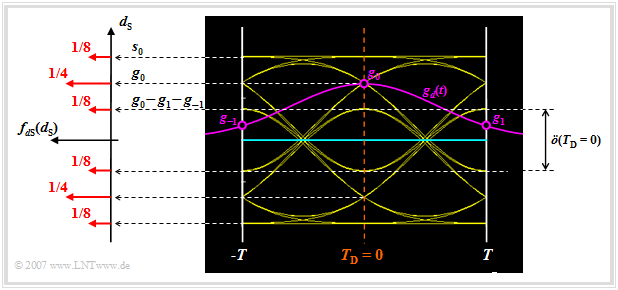
| + | Analysieren wir nun die möglichen Werte für das Detektionsnutzsignal zu den Detektionszeitpunkten: | ||
| + | *Von den insgesamt 32 Augenlinien schneiden vier die Ordinate <i>t</i> = 0 bei <i>g</i><sub>0</sub> + 2 · <i>g</i><sub>1</sub> = <i>s</i><sub>0</sub>. Diese Linien gehören zu den Amplitudenkoeffizienten „ ... , +1, +1, +1, ... ”.<br> | ||
| + | |||
| + | *Die vier Augenlinien, die jeweils die Amplitudenkoeffizienten „ ... , –1, +1, –1, ... ” repräsentieren, ergeben den Detektionsnutzabtastwert <i>d</i><sub>S</sub>(<i>T</i><sub>D</sub> = 0) = <i>g</i><sub>0</sub> – 2 · <i>g</i><sub>1</sub> = 0.36 · <i>s</i><sub>0</sub>.<br> | ||
| + | |||
| + | *Dagegen tritt der Nutzabtastwert <i>d</i><sub>S</sub>(<i>T</i><sub>D</sub> = 0) = <i>g</i><sub>0</sub> = 0.68 · <i>s</i><sub>0</sub> doppelt so häufig auf. Dieser geht auf die Amplitudenkoeffizienten „ ... , +1, +1, –1, ... ” oder „ ... , –1, +1, +1, ... ” zurück.<br> | ||
| + | |||
| + | *Für die 16 Augenlinien, welche die Ordinate <i>t</i> = 0 unterhalb der Entscheiderschwelle <i>E</i> = 0 schneiden, ergeben sich genau spiegelbildliche Verhältnisse.<br><br> | ||
| + | |||
| + | Die Konsequenzen dieser Analyse werden auf der nächsten Seite beschrieben.<br> | ||
== Next == | == Next == | ||
Version vom 24. Dezember 2016, 12:27 Uhr
Inhaltsverzeichnis
Gaußförmiges Empfangsfilter (1)
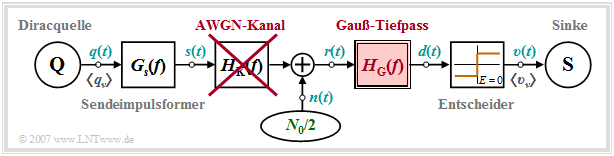
Zur quantitativen Berücksichtigung der Impulsinterferenzen wird folgende Konfiguration angenommen:
- Rechteckförmiger NRZ–Sendegrundimpuls gs(t) mit der Höhe s0 und der Dauer T,
- Gaußförmiges Empfangsfilter mit der Grenzfrequenz fG:
- \[H_{\rm E}(f) = H_{\rm G}(f) = {\rm exp}\left [- \frac{\pi \cdot f^2}{(2f_{\rm G})^2} \right ] \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm}h_{\rm E}(t) = h_{\rm G}(t) = {\rm exp}\left [- \pi \cdot (2 f_{\rm G} t)^2\right ] \hspace{0.05cm}.\]
- AWGN–Kanal, das heißt, es gilt HK(f) = 1 und Φn(f) = N0/2.
Für das gesamte Kapitel 3.2 wird somit von nachfolgendem Blockschaltbild ausgegangen.
Aufgrund der getroffenen Voraussetzungen gilt für den Detektionsgrundimpuls:
\[g_d(t) = g_s(t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot s_0 \cdot \int_{t-T/2}^{t+T/2} {\rm exp}\left [- \pi \cdot (2 \cdot f_{\rm G}\cdot \tau )^2\right ] \,{\rm d} \tau \hspace{0.05cm}.\]
Die Integration führt zu folgendem Ergebnis:
\[g_d(t) = s_0 \cdot \left [ {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \right ]\hspace{0.05cm},\]
\[g_d(t) = {s_0}/{2} \cdot \left [ {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm erfc} \left ( 2 \cdot \sqrt {\pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \right ]\hspace{0.05cm}.\]
Hierbei sind zwei Varianten der komplementären Gaußschen Fehlerfunktion verwendet, nämlich
\[\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm},\hspace{0.5cm} {\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.\]
Das Modul Komplementäre Gaußsche Fehlerfunktion liefert die Zahlenwerte von Q(x) und erfc(x).
Die Rauschleistung am Ausgang des gaußförmigen Empfangsfilters HG(f) ist gleich
\[\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0\cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.\]
Aus diesen beiden Gleichungen erkennt man bereits:
- Je kleiner die Grenzfrequenz fG des Gauß–Tiefpasses ist, desto kleiner ist der Rauscheffektivwert σd und umso besser ist demzufolge das Rauschverhalten.
- Eine kleine Grenzfrequenz führt aber zu einer starken Abweichung des Detektionsgrundimpulses gd(t) von der Rechteckform und damit zu nicht vernachlässigbaren Impulsinterferenzen.
Gaußförmiges Empfangsfilter (2)
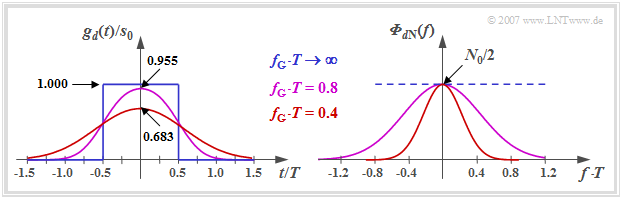
Die nachfolgend linke Grafik zeigt den Detektionsgrundimpuls gd(t) am Ausgang eines Gaußtiefpasses mit der Grenzfrequenz fG, wenn am Eingang ein NRZ–Rechteckimpuls (blauer Kurvenverlauf) anliegt.
Man erkennt aus dieser Darstellung:
- Der Gaußtiefpass HG(f) bewirkt, dass der Dektionsimpuls gd(t) gegenüber dem Sendeimpuls gs(t) verkleinert und verbreitert wird. Man spricht von Zeitdispersion.
- Diese Impulsverformung ist umso stärker, je kleiner die Grenzfrequenz fG ist. Beispielsweise wird mit fG · T = 0.4 (rote Kurve) das Impulsmaximum bereits auf etwa 68% herabgesetzt.
- Im Grenzfall fG · T → ∞ hat der Gaußtiefpass keine Wirkung ⇒ gd(t) = gs(t). Allerdings ist in diesem Fall keinerlei Rauschbegrenzung wirksam, wie aus dem rechten Bild hervorgeht.
Die Grafik auf der folgenden Seite zeigt das Detektionssignal d(t) nach dem Gaußtiefpass (vor dem Entscheider) für zwei verschiedene Grenzfrequenzen:
- Der obere Signalverlauf gilt für die (normierte) Grenzfrequenz fE · T = 0.8.
- Für den unteren Signalverlauf ist die Grenzfrequenz nur halb so groß: fE · T = 0.4.
Dargestellt sind in beiden Diagrammen gleichermaßen:
- der Anteil dS(t) ohne Berücksichtigung des Rauschens (blau),
- das gesamte Detektionssignal d(t) inklusive der Rauschkomponente (gelb),
- das Sendesignal s(t) als Referenzsignal (grün gepunktet).
Leider sind die verschiedenen Signalverläufe dieses Bildschirmabzugs sehr schwer zu erkennen, besonders in der PDF–Version. Die Bildbeschreibung folgt auf der nächsten Seite.
Gaußförmiges Empfangsfilter (3)
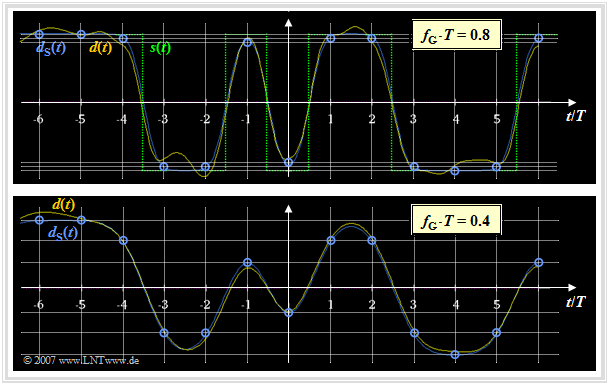
Die Grafik zeigt das Detektionssignal d(t) nach dem Gaußtiefpass (also vor dem Entscheider) für zwei verschiedene (normierte) Grenzfrequenzen, nämlich fG · T = 0.8 und fG · T = 0.4.
Durch einen Vergleich dieser Bilder lassen sich folgende Aussagen verifizieren:
- Mit der Grenzfrequenz fG · T = 0.8 (obere Grafik) ergeben sich zu den Detektionszeitpunkten (bei Vielfachen von T) nur geringfügige Impulsinterferenzen. Durch den Gaußtiefpass werden hier in erster Linie die Ecken des Sendesignals s(t) abgerundet.
- Dagegen sind im unteren Bild (fG · T = 0.4) die Auswirkungen der Impulsinterferenzen deutlich zu erkennen. Zu den Detektionszeitpunkten νT kann das blau dargestellte Detektionsnutzsignal dS(t) sechs verschiedene Werte annehmen (eingezeichnete Rasterlinien).
- Der Rauschanteil dN(t) – erkennbar als Differenz zwischen der gelben und der blauen Kurve – ist mit fG · T = 0.8 im statistischen Mittel größer als mit fG · T = 0.4.
- Dieses Ergebnis kann mit der der rechten Grafik auf der letzten Seite erklärt werden, die das Leistungsdichtespektrum der Rauschkomponente dN(t) zeigt:
- \[{\it \Phi}_{d{\rm N}}(f) = {N_0}/{2} \cdot |H_{\rm G}(f)|^2 = {N_0}/{2} \cdot {\rm exp}\left [- \frac{2\pi f^2}{(2f_{\rm G})^2} \right ] .\]
Das Integral über ΦdN(f) – also die Rauschleistung σd2 – ist für
fG · T = 0.8 (violette Kurve) doppelt so groß als mit der kleineren Grenzfrequenz fG · T = 0.4 (rote Kurve).
Definition und Aussagen des Augendiagramms
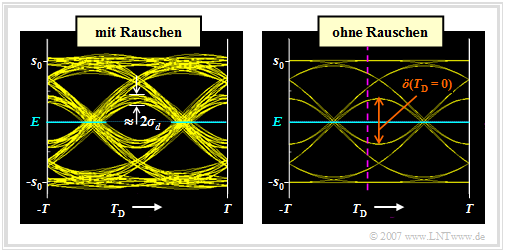
Der oben dargelegte Sachverhalt lässt sich auch am Augendiagramm erklären. Wir gehen von einem redundanzfreien binären bipolaren NRZ–Rechtecksignal s(t) und dem Gaußtiefpass mit fG · T = 0.4 aus. Dargestellt sind die Augendiagramme nach dem Gaußtiefpass, links mit Berücksichtigung des Rauschens ⇒ Signal d(t) und rechts ohne Berücksichtigung des Rauschens ⇒ Signal dS(t).
Dieses Diagramm hat eine gewisse Ähnlichkeit mit einem Auge, was zu seiner Namensgebung geführt hat. Diese Darstellung erlaubt wichtige Aussagen über die Qualität eines digitalen Übertragungssystems:
- Nur das Augendiagramm des Signals d(t) kann messtechnisch auf einem Oszilloskop dargestellt werden, das mit dem Taktsignal getriggert wird. Aus diesem Augendiagramm (linke Grafik) kann beispielsweise der Rauscheffektivwert σd abgelesen – besser gesagt: abgeschätzt – werden.
- Das Augendiagramm ohne Rauschen (rechte Grafik) bezieht sich auf das Detektionsnutzsignal dS(t) und kann nur mittels einer Rechnersimulation ermittelt werden. Für ein realisiertes System ist dieses Augendiagramm nicht darstellbar, da der Rauschanteil dN(t) nicht eliminiert werden kann.
- Bei beiden Diagrammen wurden jeweils 2048 Augenlinien gezeichnet. In der rechten Grafik sind jedoch nur 25 = 32 Augenlinien unterscheidbar, da der vorliegende Detektionsgrundimpuls gd(t) auf den Zeitbereich | t | ≤ 2T beschränkt ist (siehe frühere Grafik mit fG · T = 0.4, rote Kurve).
- Die inneren Augenlinien bestimmen die vertikale Augenöffnung ö(TD). Je kleiner diese ist, desto größer ist der Einfluss von Impulsinterferenzen. Bei einem (impulsinterferenzfreien) Nyquistsystem ist die vertikale Augenöffnung maximal. Normiert auf die Sendeamplitude gilt hier ö(TD)/s0 = 2.
- Bei symmetrischem Grundimpuls ist der Detektionszeitpunkt TD = 0 optimal. Mit einem anderen Wert (z.B. TD = – T/10) wäre ö(TD)/s0 etwas kleiner und damit die Fehlerwahrscheinlichkeit deutlich größer. Dieser Fall ist in der Grafik durch die violett–gestrichelte Vertikale angedeutet.
Mittlere Fehlerwahrscheinlichkeit (1)
Wir gehen wie bei den bisherigen Grafiken im Kapitel 3.2 von folgenden Voraussetzungen aus:
- NRZ–Rechtecke mit Amplitude s0, AWGN–Rauschen mit N0, wobei
- \[10 \cdot {\rm lg}\hspace{0.1cm} \frac{s_0^2 \cdot T}{N_0}\approx 13\,{\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{N_0}{s_0^2 \cdot T} = 0.05\hspace{0.05cm}.\]
- Gaußförmiges Empfangsfilter mit Grenzfrequenz fG · T = 0.4:
- \[\sigma_d^2 = \frac{(N_0 /T)\cdot (f_{\rm G}\cdot T)}{\sqrt{2}}= \frac{0.05 \cdot s_0^2\cdot0.4}{\sqrt{2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_d = \sqrt{0.0141}\cdot s_0 \approx 0.119 \cdot s_0 \hspace{0.05cm}.\]
- Für die Detektionsgrundimpulswerte gilt:
- \[g_0 = g_d(t=0) \approx 0.68 \cdot s_0,\]
- \[ g_1 = g_d(t=T) \approx 0.16 \cdot s_0, \hspace{0.2cm} g_{-1} = g_d(t=-T) \approx 0.16 \cdot s_0\hspace{0.05cm}.\]
Alle anderen Grundimpulswerte können vernachlässigt werden.
Analysieren wir nun die möglichen Werte für das Detektionsnutzsignal zu den Detektionszeitpunkten:
- Von den insgesamt 32 Augenlinien schneiden vier die Ordinate t = 0 bei g0 + 2 · g1 = s0. Diese Linien gehören zu den Amplitudenkoeffizienten „ ... , +1, +1, +1, ... ”.
- Die vier Augenlinien, die jeweils die Amplitudenkoeffizienten „ ... , –1, +1, –1, ... ” repräsentieren, ergeben den Detektionsnutzabtastwert dS(TD = 0) = g0 – 2 · g1 = 0.36 · s0.
- Dagegen tritt der Nutzabtastwert dS(TD = 0) = g0 = 0.68 · s0 doppelt so häufig auf. Dieser geht auf die Amplitudenkoeffizienten „ ... , +1, +1, –1, ... ” oder „ ... , –1, +1, +1, ... ” zurück.
- Für die 16 Augenlinien, welche die Ordinate t = 0 unterhalb der Entscheiderschwelle E = 0 schneiden, ergeben sich genau spiegelbildliche Verhältnisse.
Die Konsequenzen dieser Analyse werden auf der nächsten Seite beschrieben.
Next
[[Datei:||class=fit]]