Digitalsignalübertragung/Lineare digitale Modulation – Kohärente Demodulation: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 177: | Zeile 177: | ||
[[Aufgaben:1.9 BPSK und 4-QAM|A1.9 BPSK und 4-QAM]] | [[Aufgaben:1.9 BPSK und 4-QAM|A1.9 BPSK und 4-QAM]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Version vom 20. Dezember 2016, 17:42 Uhr
Inhaltsverzeichnis
- 1 Gemeinsames Blockschaltbild für ASK und BPSK
- 2 Fehlerwahrscheinlichkeit des optimalen BPSK–Systems (1)
- 3 Fehlerwahrscheinlichkeit des optimalen BPSK–Systems (2)
- 4 Fehlerwahrscheinlichkeit des optimalen ASK–Systems
- 5 Fehlerwahrscheinlichkeit bei 4–QAM und 4–PSK (1)
- 6 Fehlerwahrscheinlichkeit bei 4–QAM und 4–PSK (2)
- 7 Phasenversatz zwischen Sender und Empfänger
- 8 Basisbandmodell für ASK und BPSK (1)
- 9 Basisbandmodell für ASK und BPSK (2)
- 10 Aufgaben
Gemeinsames Blockschaltbild für ASK und BPSK
Im Kapitel 4.2 des Buches „Modulationsverfahren” wurden die digitalen Trägerfrequenzsysteme ASK (Amplitude Shift Keying) und BPSK (Binary Phase Shift Keying) bereits ausführlich beschrieben. In diesem Kapitel wird nun die Fehlerwahrscheinlichkeit dieser Systeme berechnet, wobei von dem folgenden gemeinsamen Blockschaltbild ausgegangen wird:
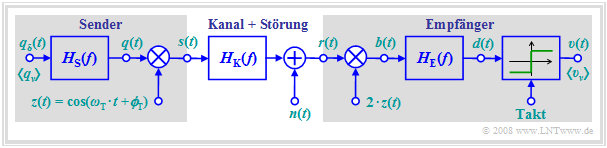
Wie im Kapitel 4.2 des Buches „Modulationsverfahren” gelten auch hier folgende Voraussetzungen:
- Die Demodulation geschieht stets kohärent. Das heißt: Beim Empfänger wird ein Trägersignal mit gleicher Frequenz wie beim Sender zugesetzt, aber mit doppelter Amplitude. Der Phasenversatz sei zunächst ΔϕT = 0.
- Bei BPSK wird von den bipolaren Amplitudenkoeffizienten aν ∈ {–1, +1} ausgegangen und die Entscheiderschwelle liegt bei E = 0. Dagegen gilt bei ASK aν ∈ {0, 1}. Die Entscheiderschwelle E ist für diesen unipolaren Fall bestmöglich zu wählen.
- Wir betrachten stets den AWGN–Kanal, das heißt, dass für den Kanalfrequenzgang HK(f) = 1 gilt und n(t) weißes Gaußsches Rauschen mit der (einseitigen) Rauschleistungsdichte N0 darstellt.
- Die Entzerrung linearer Kanalverzerrungen – also der Fall HK(f) ≠ const. – ist in gleicher Weise möglich wie bei der Basisbandübertragung. Hierzu sei auf das Kapitel 3.3 verwiesen.
Fehlerwahrscheinlichkeit des optimalen BPSK–Systems (1)
Wir gehen zunächst von einem bipolaren rechteckförmigen Quellensignal q(t) mit der Amplitude ±s0 aus. Dessen normiertes Spektrum lautet: HS(f) = si(πfT). Ebenso wie bei der Basisbandübertragung ergibt sich die kleinstmögliche Bitfehlerwahrscheinlichkeit für das Empfangsfilter HE(f) = HS∗(f) = si(πfT).
Die Signalverläufe des BPSK–Systems mit Matched–Filter–Empfänger zeigen:
- Das Detektionsnutzsignal dS(t) – also ohne Rauschanteil – ist zu allen Detektionszeitpunkten νT stets ±s0, wobei das Vorzeichen durch die Amplitudenkoeffizienten aν festgelegt sind.
- Wie beim vergleichbaren Basisbandsystem beträgt die Fehlerwahrscheinlichkeit <nobr>pB = Q(s0/σd),</nobr> wobei Q(x) das komplementäre Gaußsche Fehlerintergral Please add link bezeichnet.
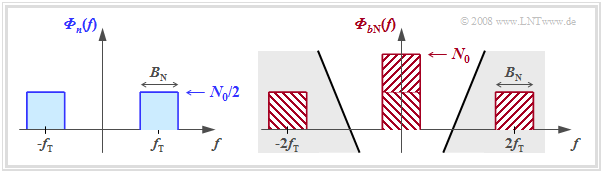
- Unterschiedlich zum Basisbandsystem ist jedoch die Rauschleistung. Der Rauschanteil bN(t) ergibt sich durch die Multiplikation des Bandpassrauschens n(t) mit dem Träger 2 · cos(2π fT t) und besitzt die Rauschleistungsdichte
- \[{{\it \Phi}_{b{\rm N}}(f)}={{\it \Phi}_{n}(f)}\star \left[ 1^2 \cdot \delta ( f - f_{\rm T})+ 1^2 \cdot \delta ( f + f_{\rm T})\right].\]
- Die nachfolgende Grafik verdeutlicht diese Gleichung am Beispiel von bandbegrenztem weißen Rauschen mit der Bandbreite Bn. Während Φn(f = fT) gleich N0/2 gilt, ist ΦbN(f = 0) = N0. Die Anteile um ±2fT werden durch das nachfolgende Empfangsfilter HE(f) eliminiert und spielen für die weiteren Betrachtungen keine Rolle.
- Bei echt weißem Rauschen gilt mit dem Grenzübergang Bn → ∞ \[{{\it \Phi}_{n}(f)}={N_0}/{2}, \hspace{0.3cm}{{\it
\Phi}_{b{\rm N}}(f)}={N_0}.\]
Fehlerwahrscheinlichkeit des optimalen BPSK–Systems (2)
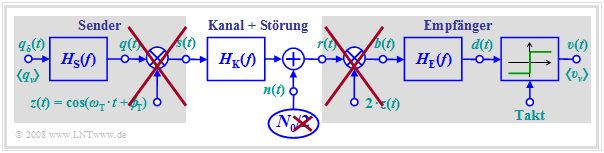
Die gerade durchgeführten Betrachtungen zeigen, dass man zur Berechnung der Fehlerwahrscheinlichkeit des BPSK–Systems auf die beiden Multiplikationen mit z(t) und 2 · z(t) verzichten kann, wenn man die Rauschleistung verdoppelt.
Damit ergibt sich für die Rauschleistung vor dem Entscheider bei AWGN–Rauschen:\[{\sigma_d}^2 = N_0 \cdot \int_{-\infty}^{+\infty} {\rm
si}^2(\pi \hspace{0.01cm} f \hspace{0.05cm} T_{\rm B}) \,{\rm d} f
= {N_0}/{T_{\rm B}},\]
also der doppelte Wert als bei der Basisbandübertragung. Hinweis: Um später einen Vergleich mit der QAM zu ermöglichen, wurde hier die Symboldauer T durch die Bitdauer TB ersetzt. Bei BPSK (und auch bei ASK) sind T und TB gleich.
Damit lautet die BPSK–Fehlerwahrscheinlichkeit mit den zwei üblichen Gaußschen Fehlerfunktionen: Please add link:\[p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{N_0 }}\hspace{0.1cm} \right
) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{2 \cdot N_0 }}\hspace{0.1cm} \right
).\]
Berücksichtigt man weiter, dass die bei BPSK aufgewandte Energie pro Bit
\(E_{\rm B} = {1}/{2}\cdot s_0^2 \cdot T_{\rm B}\)
beträgt, so kann diese Gleichung wie folgt umgeformt werden:\[p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right
) ={1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right
).\]
Es ergibt sich somit genau die gleiche Formel wie bei der Basisbandübertragung, bei der jedoch für die „Energie pro Bit” EB = s02 · TB zu verwenden war und nicht wie hier EB = 1/2 · s02 · TB.
Anmerkung: Diese letzte Gleichung gilt nicht nur bei Rechteck–Quellensignal
⇒ HS(f) = si(πft), sondern für jedes beliebige HS(f), solange
- das Empfangsfilter HE(f) = HS∗(f) exakt an den Sender angepasst ist,
- das Produkt HS(f) · HE(f) das erste Nyquistkriterium erfüllt.
Fehlerwahrscheinlichkeit des optimalen ASK–Systems
Wir betrachten nun ein ASK–System bei gleichen Voraussetzungen wie das BPSK–System. Hier sind alle Detektionsnutzsignalwerte dS(νT) entweder 0 oder s0, ist dementsprechend der Abstand von der Schwelle E = s0/2 jeweils s0/2, ist der Rauscheffektivwert σd genau so groß wie bei BPSK, ist die Energie pro Bit nur halb so groß wie bei BPSK:\[E_{\rm B} = {1}/{4}\cdot s_0^2 \cdot T_{\rm B}.\]
Damit lauten die entsprechenden Gleichungen für die Bitfehlerwahrscheinlichkeit:\[p_{\rm B} = {\rm Q}\left ( \frac{s_0/2}{\sigma_d } \right
)= {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T_{\rm B}}{4 \cdot N_0 }} \hspace{0.1cm}\right
),\]
\[p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right
) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right
).\]
Die Grafik zeigt die Fehlerwahrscheinlichkeiten von ASK und BPSK abhängig vom Quotienten EB/N0.
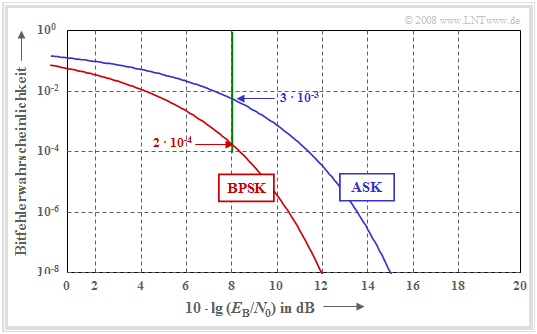
Man erkennt aus dieser doppelt–logarithmischer Darstellung:
- Die ASK–Kurve liegt um 3 dB rechts von der BPSK–Kurve. Für die Fehlerwahrscheinlichkeit 10–8 benötigt man bei BPSK etwa 10 · lg (EB/N0) = 12 dB, bei ASK dagegen ca. 15 dB.
- Der Systemvergleich bei dem festen Abszissenwert 10 · lg (EB/N0) = 8 dB liefert die beiden Bitfehlerwahrscheinlichkeiten 2 · 10–4 (für BPSK) bzw. 6 · 10–3 (für ASK).
Fehlerwahrscheinlichkeit bei 4–QAM und 4–PSK (1)
Im Kapitel 4.3 des Buches „Modulationsverfahren” wurde die Quadraturamplitudenmodulation (QAM) ausführlich beschrieben. Dem Blockschaltbild ist zu entnehmen:
- Die 4–QAM kann durch zwei zueinander orthogonale BPSK–Systeme mit Cosinus– bzw. Minus–Sinus–Träger dargestellt werden.
- Das binäre Quellensignal q(t) mit der Bitdauer TB ⇒ Bitrate RB wird in zwei Teilsignale qI(t) und qQ(t) mit jeweils halber Rate aufgespaltet (Seriell–Parallel–Wandlung). Die Symboldauer von qI(t) bzw. qQ(t) beträgt jeweils T = 2 · TB, die Symbolrate jeweils RB/2.
- Die Amplituden der beiden orthogonalen Trägersignale sind um den Faktor „Wurzel aus 2” kleiner gewählt als bei der BPSK, so dass die Hüllkurve des Sendesignals s(t) wiederum s0 beträgt.
Die Fehlerwahrscheinlichkeit der QAM ist die gleiche wie die der zwei orthogonalen BPSK–Systemen. Wegen der kleineren Signalamplitude und der niedrigeren Symbolrate gilt:
\[p_{\rm B} = {\rm Q}\left ( \frac{s_0/\sqrt{2}}{\sigma_d } \right
) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\sigma_d}^2 = \frac{N_0 }{2 \cdot T_{\rm B}}\]
\[\Rightarrow \hspace{0.3cm}p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{s_0^2 }{2} \cdot \frac{2 \cdot T_{\rm B} }{N_0}}\hspace{0.1cm}\right
)= {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right
).\]
Das heißt: Obwohl mit der 4–QAM gegenüber der BPSK die doppelte Informationsmenge übertragen werden kann, ergibt sich in Abhängigkeit von EB/N0 die genau gleiche Bitfehlerwahrscheinlichkeit. Berücksichtigt ist hierbei, dass auch bei der 4–QAM für die mittlere Energie pro Bit gilt:\[E_{\rm B} = {1}/{2}\cdot s_0^2 \cdot T_{\rm B}.\]
Da sich die quaternäre Phasenmodulation (4–PSK) von der 4–QAM nur um eine Phasenverdrehung von 45° unterscheidet, ergibt sich auch für diese bei Berücksichtigung geeigneter Entscheidungsgebiete die gleiche Fehlerwahrscheinlichkeit.
Fehlerwahrscheinlichkeit bei 4–QAM und 4–PSK (2)
Die obere Grafik zeigt die Phasendiagramme der BPSK mit Cosinus– bzw. Minus–Sinusträger, jeweils für 10 · lg EB/N0 = 6 dB. Hinweis: In der linken (bzw. rechten) Grafik erkennt man Bitfehler durch gelbe Kreuze rechts (bzw. oberhalb) der Entscheiderschwelle. Zur besseren Kenntlichmachung sind Bitfehler durch Kreise hervorgehoben, zum Beispiel gelbe Punkte rechts bzw. oberhalb der Schwelle.
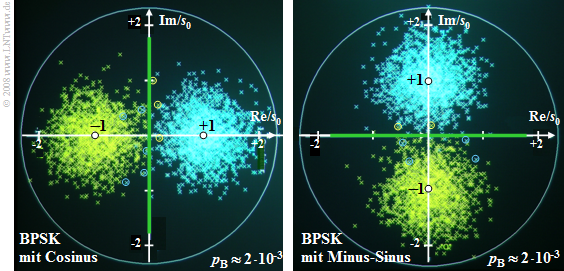
Der Abstand der Nutzabtastwerte ohne Rauschen (markiert durch die weißen Punkte) von der jeweiligen Entscheiderschwelle (grün markiert) beträgt jeweils s0. Die Varianz der Detektionsabtastwerte – erkennbar an den Punktwolken – ist gleich
\[{\sigma_d}^2 = \frac{N_0 }{ T_{\rm B}}= \frac{s_0^2/2 }{ E_{\rm
B}/N_0},\hspace{0.3cm}{\rm wegen}\hspace{0.2cm}E_{\rm B} = {1}/{2}\cdot s_0^2 \cdot T_{\rm
B}.\]
Mit 10 · lg EB/N0 = 6 dB ⇒ EB/N0 = 100.6 ≈ 4 ergibt sich daraus:\[{{\sigma_d}^2 }/{ {s_0}^2}= [{ 2 \cdot 10^{0.6}}]^{-1}
\approx 0.125\hspace{0.3cm}\Rightarrow \hspace{0.3cm}
{{\sigma_d} }/{ {s_0}}\approx 0.35\]
\(\Rightarrow \hspace{0.5cm}p_{\rm B} = {\rm Q}\left ( s_0/{\sigma_d } \right
)= {\rm Q}\left ( \sqrt{2 \cdot 10^{0.6}} \hspace{0.08cm}\right )
= {\rm Q}(2.8) \approx 2 \cdot 10^{-3}.\)
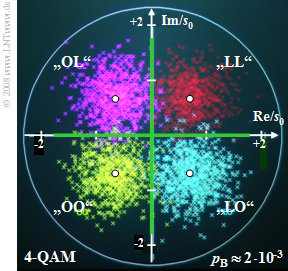
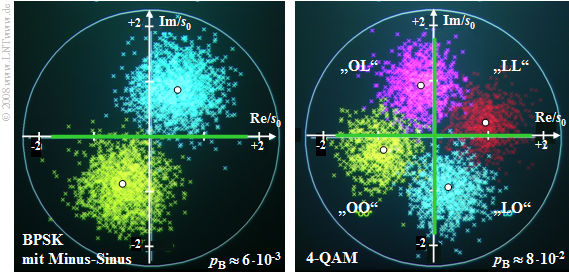
Das untere Bild gilt für die 4–QAM, die man als zwei orthogonale BPSK–Systeme mit Cosinus– und Minus–Sinusträger auffassen kann.
- Der Abstand der nunmehr vier Nutzabtastwerte ohne Rauschen (markiert durch weiße Punkte) vom Ursprung ist wieder s0.
- Der Abstand zu den Entscheiderschwellen ist nun allerdings um den Faktor „Wurzel aus 2” geringer als bei BPSK, aber auch der Rauscheffektivwert σd ist um den gleichen Faktor kleiner.
- Die Bitfehlerwahrscheinlichkeit für 4–QAM und BPSK ist somit exakt gleich: pB = 2 · 10–3.
Phasenversatz zwischen Sender und Empfänger
Voraussetzung für die Gültigkeit der bisherigen Gleichungen ist eine strenge Synchronität zwischen den bei Sender und Empfänger zugesetzten Trägersignalen. Nun wird ein Phasenversatz ΔϕT zwischen den beiden Trägersignalen angenommen, während weiterhin von Frequenzsynchronität ausgegangen wird.
Die Grafik zeigt die Phasendiagramme für ΔϕT = 30°. Man erkennt:
- Sowohl bei BPSK (links) als auch bei der 4–QAM (rechts) bewirkt ein Phasenversatz um ΔϕT eine Drehung des Phasendiagramms.
- Bei BPSK bewirkt der Phasenversatz ein um cos(ΔϕT) kleineres Nutzsignal. Den gleichen Effekt haben wir bereits beim Synchrondemodulator eines analogen Übertragungssystems festgestellt.
- Demzufolge wird auch der Abstand des Detektionsnutzsignals von der Entscheiderschwelle um den gleichen Faktor geringer, was zu einer höheren Fehlerwahrscheinlichkeit führt:\[p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\cdot \cos({\rm \Delta} \phi_{\rm T})\right
) .\]
Mit den hier zugrundeliegenden Zahlenwerten (10 · lg EB/N0 = 6 dB, ΔϕT = 30°) erhöht sich die Fehlerwahrscheinlichkeit der BPSK von 0.2% auf etwa 0.6%. Dagegen wird bei der 4–QAM (rechtes Diagramm) die Fehlerwahrscheinlichkeit mit ϕT = 30° nahezu um den Faktor 40 größer (pB ≈ 8%). Allgemein gilt hier für die 4–QAM, falls |ΔϕT| < 45°, wie in Aufgabe A1.9 gezeigt werden soll:\[p_{\rm B} = \frac{1}{2} \cdot {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\cdot
\frac{\cos(45^\circ)}{\cos(45^\circ+{\rm \Delta} \phi_{\rm
T})}\right) + \frac{1}{2} \cdot {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\cdot
\frac{\cos(45^\circ)}{\cos(45^\circ-{\rm \Delta} \phi_{\rm
T})}\right)
.\]
Fazit: Obwohl man mit der 4–QAM über den gleichen Kanal die doppelte Information wie bei BPSK übertragen kann, weisen bei idealen Bedingungen beide Systeme die gleiche Übertragungsqualität (Fehlerwahrscheinlichkeit) auf. Bei nicht idealen Bedingungen – zum Beispiel einem Phasenversatz – steigt allerdings die Fehlerwahrscheinlichkeit der 4–QAM sehr viel stärker an als bei der BPSK.
Basisbandmodell für ASK und BPSK (1)
Die Grafik zeigt oben nochmals das Gesamtblockschaltbild eines Trägerfrequenzsystems mit kohärenter Demodulation, das für ASK (unipolare Amplitudenkoeffizienten) und BPSK (bipolare Koeffizienten) in gleicher Weise gültig ist. Durch die Multiplikation mit dem Trägersignal z(t) wird das Spektrum Q(f) des Quellensignals – und dementsprechend auch das Leistungsdichtespektrum Φq(f) – um die Trägerfrequenz ±fT beidseitig verschoben. Nach dem Kanal wird diese Verschiebung durch den Synchrondemodulator wieder rückgängig gemacht.
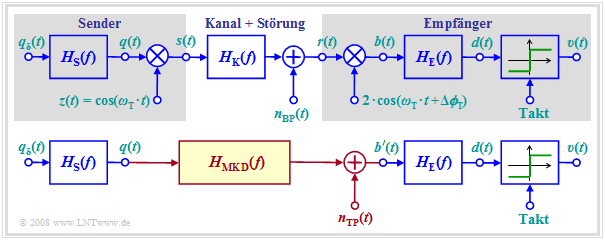
Geht man vom äquivalenten Basisbandmodell entsprechend der unteren Grafik aus, so lässt sich die Berechnung der Signale nach dem Demodulator vereinfachen:
- Man kürzt quasi den Einfluss von Modulator und Demodulator und ersetzt den Bandpasskanal mit dem Frequenzgang HK(f) durch eine geeignete Tiefpass–Übertragungsfunktion HMKD(f), wobei der Index für „Modulator–Kanal– Demodulator” steht.
- Unter Berücksichtigung einer Phasendifferenz ΔϕT zwischen den Trägersignalen von Sender und Empfänger erhält man für die resultierende Übertragungsfunktion:
- \[H_{\rm MKD}(f) = \frac{1}{2} \cdot \left [ {\rm e}^{\hspace{0.04cm}-{\rm j} \hspace{0.04cm}\cdot \hspace{0.04cm}{\rm \Delta} \phi_{\rm T}} \cdot H_{\rm K}(f-f_{\rm T}) +{\rm e}^{\hspace{0.04cm}{\rm j} \hspace{0.04cm}\cdot \hspace{0.04cm}{\rm \Delta} \phi_{\rm T}} \cdot H_{\rm K}(f+f_{\rm T})\right ] .\]
- Bei einem reellen und um die Trägerfrequenz fT symmetrischen Kanalfrequenzgang HK(f) – also falls HK(fT – f) = HK(fT + f) gilt – kann man diese Gleichung wie folgt vereinfachen:
- \[H_{\rm MKD}(f) = \frac{\cos({\rm \Delta} \phi_{\rm T})}{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] .\]
Die Bitfehlerwahrscheinlichkeiten von ASK und BPSK können somit auch mit dem einfacheren Basisbandmodell berechnet werden, und zwar auch dann, wenn ein verzerrender Kanal HK(f) vorliegt. Zu beachten ist, dass auch das Rauschsignal n(t) in den Tiefpassbereich transformiert werden muss. Bei weißem Rauschen muss hierzu Φn(f) = N0/2 durch Φn,TP (f) = N0 ersetzt werden.
Basisbandmodell für ASK und BPSK (2)
Die Grafik verdeutlicht das Basisbandmodell anhand der Amplitudenspektren, wobei vereinfachend
- ein gaußförmiges Q(f),
- BPSK–Modulation,
- ein rechteckförmiger Bandpasskanal HK(f),
- phasensynchrone Demodulation, und
- ein ebenfalls rechteckförmiges Empfangsfilter HE(f) mit ΔfE > ΔfK
vorausgesetzt werden.
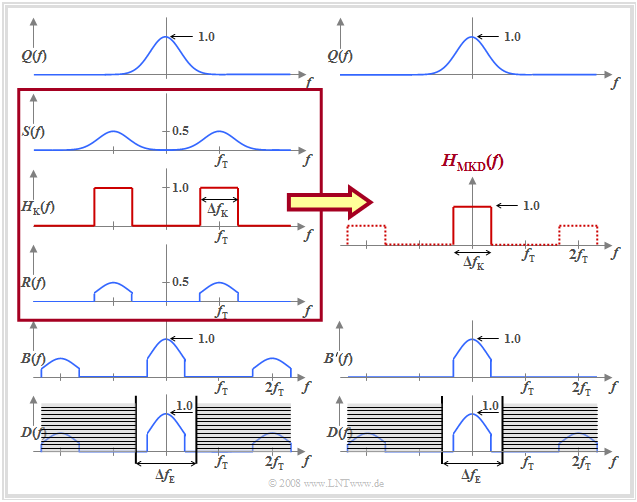
Man erkennt:
- Das Spektrum D(f) wird durch das äquivalente Basisbandmodell richtig wiedergegeben, obwohl sich die Spektren B(f) bzw. B'(f) um die doppelte Trägerfrequenz unterscheiden.
- Die resultierende Übertragungsfunktion HMKD(f) berücksichtigt auch die Bandbegrenzung durch den Kanal, der in diesem Beispiel als rechteckförmig um die Trägerfrequenz angenommen wurde.
Aufgaben
Zusatzaufgaben:1.8 BPSK-Fehlerwahrscheinlichkei