Digitalsignalübertragung/Eigenschaften von Nyquistsystemen: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 27: | Zeile 27: | ||
T}\right)</math><br> | T}\right)</math><br> | ||
mit trapezförmigem Spektrum und dem Rolloff–Faktor <i>r</i> = 0.5 zugrunde liegt. Dieser wurde bereits im [http://www.lntwww.de/Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation Kapitel 3] des Buches „Signaldarstellung” behandelt.{{end}} | mit trapezförmigem Spektrum und dem Rolloff–Faktor <i>r</i> = 0.5 zugrunde liegt. Dieser wurde bereits im [http://www.lntwww.de/Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation Kapitel 3] des Buches „Signaldarstellung” behandelt.{{end}} | ||
| + | |||
| + | |||
| + | == Erstes Nyquistkriterium im Frequenzbereich == | ||
| + | <br> | ||
| + | Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.<br> | ||
| + | Erstes Nyquistkriterium: Erfüllt das Spektrum <i>G<sub>d</sub></i>(<i>f</i>) des Detektionsgrundimpulses die Bedingung<br> | ||
| + | <math>\sum_{k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= | ||
| + | g_0 \cdot T = {\rm const.} \hspace{0.05cm}, </math><br> | ||
| + | so ist <i>g<sub>d</sub></i>(<i>t</i>) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten | ||
| + | <i>νT</i> (<i>ν</i> ≠ 0) und der Amplitude <i>g<sub>d</sub></i>(<i>t</i> = 0) = <i>g</i><sub>0</sub>. <i>Hinweis</i>: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.<br> | ||
| + | Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum<br> | ||
| + | <math>G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\ | ||
| + | 0 \\ \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm{f\ddot{u}r}} | ||
| + | \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} | ||
| + | |f| < {1}/({2T})\hspace{0.05cm}, \\ | ||
| + | |f| > {1}/({2T}) \hspace{0.1cm} \\ | ||
| + | \end{array}</math><br> | ||
| + | erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls <i>g</i><sub>1</sub>(<i>t</i>) = <i>g</i><sub>0</sub> · si(π<i>t</i>/<i>T</i>) klingt sehr langsam ab, nämlich asymptotisch mit 1/<i>t</i>.<br> | ||
| + | [[Datei:P_ID1273__Dig_T_1_3_S2_v1.png|Zur Verdeutlichung des ersten Nyquistkriteriums|class=fit]]<br> | ||
| + | Der rechts oben dargestellte Realteil des Spektrums <i>G</i><sub>2</sub>(<i>f</i>) wurde aus dem Rechteckspektrum <i>G</i><sub>1</sub>(<i>f</i>) durch Verschiebung von Teilstücken um 1/<i>T</i> nach rechts oder links konstruiert. Wegen <br> | ||
| + | <math>\sum_{k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f - | ||
| + | \frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm}, | ||
| + | \hspace{1cm}\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f - | ||
| + | \frac{k}{T} \right)\right]= 0</math><br> | ||
| + | handelt es sich bei <i>G</i><sub>2</sub>(<i>f</i>) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/<i>T</i> auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses <i>g</i><sub>2</sub>(<i>t</i>) ist allerdings sehr kompliziert. | ||
{{Display}} | {{Display}} | ||
Version vom 21. November 2016, 14:46 Uhr
Erstes Nyquistkriterium im Zeitbereich
Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals
\(d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)\)
zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls gd(t)
- auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
- äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.
Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal dN(t) als vernachlässigbar klein angenommen.
- \[g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\]
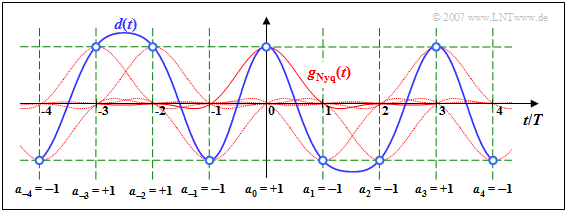
Zu den Detektionszeitpunkten gilt d(νT) = aν · gNyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a0 nicht.
Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls
\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot
t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot
T}\right)\)
Erstes Nyquistkriterium im Frequenzbereich
Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.
Erstes Nyquistkriterium: Erfüllt das Spektrum Gd(f) des Detektionsgrundimpulses die Bedingung
\(\sum_{k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)=
g_0 \cdot T = {\rm const.} \hspace{0.05cm}, \)
so ist gd(t) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten
νT (ν ≠ 0) und der Amplitude gd(t = 0) = g0. Hinweis: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.
Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum
\(G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\
0 \\ \end{array} \right.\quad
\begin{array}{*{1}c} {\rm{f\ddot{u}r}}
\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}
|f| < {1}/({2T})\hspace{0.05cm}, \\
|f| > {1}/({2T}) \hspace{0.1cm} \\
\end{array}\)
erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls g1(t) = g0 · si(πt/T) klingt sehr langsam ab, nämlich asymptotisch mit 1/t.
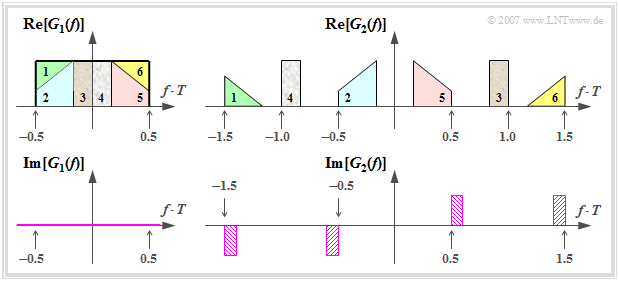
Der rechts oben dargestellte Realteil des Spektrums G2(f) wurde aus dem Rechteckspektrum G1(f) durch Verschiebung von Teilstücken um 1/T nach rechts oder links konstruiert. Wegen
\(\sum_{k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f -
\frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm},
\hspace{1cm}\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f -
\frac{k}{T} \right)\right]= 0\)
handelt es sich bei G2(f) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/T auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses g2(t) ist allerdings sehr kompliziert.