Digitalsignalübertragung/Eigenschaften von Nyquistsystemen: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 21: | Zeile 21: | ||
{{Beispiel}}''':''' Die Grafik zeigt das Detektionssignal <i>d</i>(<i>t</i>) eines solchen Nyquistsystems. Rot gepunktet sind die (gewichteten und verschobenen) Nyquistimpulse <i>a</i><sub>ν</sub> · <i>g</i><sub>Nyq</sub>(<i>t</i> – <i>νT</i>) eingezeichnet. <br> | {{Beispiel}}''':''' Die Grafik zeigt das Detektionssignal <i>d</i>(<i>t</i>) eines solchen Nyquistsystems. Rot gepunktet sind die (gewichteten und verschobenen) Nyquistimpulse <i>a</i><sub>ν</sub> · <i>g</i><sub>Nyq</sub>(<i>t</i> – <i>νT</i>) eingezeichnet. <br> | ||
[[Datei:P_ID1272__Dig_T_1_3_S1_v1.png|Detektionssignal bei Nyquistimpulsformung|class=fit]]<br> | [[Datei:P_ID1272__Dig_T_1_3_S1_v1.png|Detektionssignal bei Nyquistimpulsformung|class=fit]]<br> | ||
| − | Zu den Detektionszeitpunkten gilt <i>d</i>(<i>ν</i><i>T</i>) = <i>a<sub>ν</sub></i> · <i>g</i><sub>Nyq</sub>(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (<i>ν</i> < 0) sowie die Vorläufer der nachfolgenden Impulse (<i>ν</i> > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols <i>a</i><sub>0</sub> nicht.<br> | + | Zu den Detektionszeitpunkten gilt <i>d</i>(<i>ν</i><i>T</i>) = <i>a<sub>ν</sub></i> · <i>g</i><sub>Nyq</sub>(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (<i>ν</i> < 0) sowie die Vorläufer der nachfolgenden Impulse (<i>ν</i> > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols <i>a</i><sub>0</sub> nicht.<br><br> |
Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls | Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls | ||
<math>g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot | <math>g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot | ||
t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot | t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot | ||
T}\right)</math> | T}\right)</math> | ||
| − | mit trapezförmigem Spektrum und dem Rolloff–Faktor <i>r</i> = 0.5 zugrunde liegt. Dieser wurde bereits im [http://www.lntwww.de/Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation Kapitel 3] des Buches „Signaldarstellung” behandelt. | + | mit trapezförmigem Spektrum und dem Rolloff–Faktor <i>r</i> = 0.5 zugrunde liegt. Dieser wurde bereits im [http://www.lntwww.de/Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation Kapitel 3] des Buches „Signaldarstellung” behandelt.{{end}} |
{{Display}} | {{Display}} | ||
Version vom 21. November 2016, 14:22 Uhr
Erstes Nyquistkriterium im Zeitbereich
Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals
\(d(t) = \sum_{(\nu)} a_\nu \cdot g_d ( t - \nu T)\)
zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls gd(t)
- auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
- äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.
Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal dN(t) als vernachlässigbar klein angenommen.
\(g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\)
als Nyquistimpuls gNyq(t), benannt nach dem Physiker Harry Nyquist.
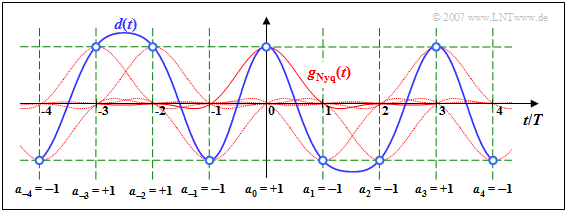
Zu den Detektionszeitpunkten gilt d(νT) = aν · gNyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a0 nicht.
Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls
\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot
t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot
T}\right)\)