Digitalsignalübertragung/Fehlerwahrscheinlichkeit bei Basisbandübertragung: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 11: | Zeile 11: | ||
Die Grafik zeigt ein sehr einfaches, aber allgemeingültiges Modell eines binären Übertragungssystems. | Die Grafik zeigt ein sehr einfaches, aber allgemeingültiges Modell eines binären Übertragungssystems. | ||
| − | [[Datei:P_ID1258__Dig_T_1_2_S1_v1.png|left| | + | [[Datei:P_ID1258__Dig_T_1_2_S1_v1.png|left|1000px]]<br> |
Dieses lässt sich wie folgt charakterisieren: | Dieses lässt sich wie folgt charakterisieren: | ||
*Die Quelle und die Sinke werden durch die beiden Binärfolgen 〈<i>q<sub>ν</sub></i>〉 und 〈<i>υ<sub>ν</sub></i>〉 beschrieben. | *Die Quelle und die Sinke werden durch die beiden Binärfolgen 〈<i>q<sub>ν</sub></i>〉 und 〈<i>υ<sub>ν</sub></i>〉 beschrieben. | ||
Version vom 16. November 2016, 17:59 Uhr
Definition der Bitfehlerwahrscheinlichkeit
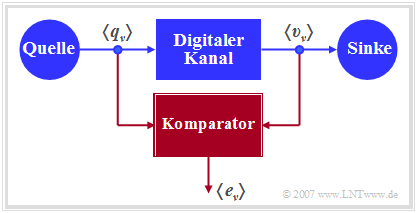
Die Grafik zeigt ein sehr einfaches, aber allgemeingültiges Modell eines binären Übertragungssystems.
Dieses lässt sich wie folgt charakterisieren:
- Die Quelle und die Sinke werden durch die beiden Binärfolgen 〈qν〉 und 〈υν〉 beschrieben.
- Das gesamte Übertragungsystem – bestehend aus Sender, Übertragungskanal inklusive Störungen und Empfänger – wird als „Black Box” mit binärem Ein– und Ausgang betrachtet.
- Dieser „Digitale Kanal” wird allein durch die Fehlerfolge 〈eν〉 charakterisiert. Bei fehlerfreier Übertragung des ν–ten Bits (υν = qν) gilt eν = 0, andernfalls (υν ≠ qν) wird eν = 1 gesetzt.
\(\it p_{\rm B} = \rm E[\rm Pr(\it v_{\nu} \ne q_{\nu})]= \overline {\rm Pr(\it v_{\nu} \ne q_{\nu})} = \lim_{{\it N}\to\infty}\frac{\rm 1}{\it N}\cdot\sum\limits_{\it \nu=\rm 1}^{\it N}\rm \rm Pr(\it v_{\nu} \ne q_{\nu})\hspace{0.05cm}.\)
Diese statistische Größe ist das wichtigste Beurteilungskriterium eines jeden Digitalsystems.
Die Berechnung als Erwartungswert E[…..] gemäß dem ersten Teil der obigen Gleichung entspricht einer Scharmittelung über die Verfälschungswahrscheinlichkeit Pr(υν ≠ qν) des ν–ten Symbols, während die überstreichende Linie im rechten Teil eine Zeitmittelung kennzeichnet. Beide Berechnungsarten führen – unter der gerechtfertigten Annahme ergodischer Prozesse – zum gleichen Ergebnis, wie im Kapitel 4 des Buches „Stochastische Signaltheorie” gezeigt wurde.
Auch aus der Fehlerfolge 〈eν〉 lässt sich die Bitfehlerwahrscheinlichkeit als Erwartungswert bestimmen, wobei zu berücksichtigen ist, dass eν nur die Werte 0 und 1 annehmen kann:\[\it p_{\rm B} = \rm E[\rm Pr(\it e_{\nu}=\rm 1)]= {\rm E}[{\it e_{\nu}}]\hspace{0.05cm}.\] Die obige Definition der Bitfehlerwahrscheinlichkeit gilt unabhängig davon, ob es statistische Bindungen innerhalb der Fehlerfolge 〈eν〉 gibt oder nicht. Je nachdem ist der Aufwand zur Berechnung von pB unterschiedlich groß und bei einer Systemsimulation müssen unterschiedliche digitale Kanalmodelle herangezogen werden. Im Kapitel 5 wird gezeigt, dass das sog. BSC–Modell (Binary Symmetrical Channel) statistisch unabhängige Fehler liefert, während für die Beschreibung von Bündelfehlerkanälen auf die Modelle von Gilbert–Elliott: .: Capacity of Burst–Noise Channel, In: Bell Syst. Techn. J. Vol. 39, 1960, pp. 1253–1266 and McCullough : The Binary Regenerative Channel, In: Bell Syst. Techn. J. (47), 1968 zurückgegriffen werden muss.