Aufgaben:Aufgabe 1.4: Maximum–Likelihood–Entscheidung: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 63: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig ist die <u>Antwort 3</u>: | + | '''(1)''' Richtig ist die <u>Antwort 3</u> ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$: |
| − | *Die Hamming–Distanzen zwischen dem spezifischen Empfangswort $\underline{y} = (1, 0, 0, 0, 1)$ und den vier möglichen Codeworten $\underline{x}_{i}$ ergeben sich wie folgt: | + | *Die Hamming–Distanzen zwischen dem spezifischen Empfangswort $\underline{y} = (1, 0, 0, 0, 1)$ und den vier möglichen Codeworten $\underline{x}_{i}$ ergeben sich wie folgt: |
:$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$ | :$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$ | ||
| − | *Entschieden wird sich für die Folge mit der geringsten Hamming–Distanz $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$. | + | *Entschieden wird sich für die Folge mit der geringsten Hamming–Distanz $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$. |
| − | '''(2)''' Für $\underline{y} = (0, 0, 0, 1, 0)$ sind die <u>Antworten 1 und 2</u> richtig, wie die folgende Rechnung zeigt: | + | '''(2)''' Für $\underline{y} = (0, 0, 0, 1, 0)$ sind die <u>Antworten 1 und 2</u> richtig, wie die folgende Rechnung zeigt: |
:$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$ | :$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$ | ||
| − | '''(3)''' Richtig ist die <u>Antwort 3</u>: | + | '''(3)''' Richtig ist die <u>Antwort 3</u>: |
| − | *Entsprechend der Hamming–Distanz wäre eine Entscheidung zugunsten von $x_{2}$ genau so möglich wie für $x_{3}$, wenn | + | *Entsprechend der Hamming–Distanz wäre eine Entscheidung zugunsten von $x_{2}$ genau so möglich wie für $x_{3}$, wenn $\underline{y} = (1, 0, 1, 1, 1)$ empfangen wird: |
:$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$ | :$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$ | ||
| − | *Der Empfangsvektor $\underline{y}$ unterscheidet sich aber von $x_{2}$ bezüglich des vierten Bits und von $x_{3}$ im zweiten Bit. | + | *Der Empfangsvektor $\underline{y}$ unterscheidet sich aber von $x_{2}$ bezüglich des vierten Bits und von $x_{3}$ im zweiten Bit. |
| − | * Da das vierte Bit unsicherer ist als das zweite, wird er sich für $x_{2}$ entscheiden . | + | * Da das vierte Bit unsicherer ist als das zweite, wird er sich für $x_{2}$ entscheiden . |
| − | '''(4)''' Da es sich hier um einen systematischen Code handelt, ist die Entscheidung für $\underline{z} = (1, 0, 1, 0, 1)$ gleichbedeutend mit der Entscheidung | + | '''(4)''' Da es sich hier um einen systematischen Code handelt, ist die Entscheidung für $\underline{z} = (1, 0, 1, 0, 1)$ gleichbedeutend mit der Entscheidung |
:$$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$ | :$$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$ | ||
| − | *Es ist nicht sicher, dass $\underline{u} = (1, 0)$ tatsächlich gesendet wurde. | + | *Es ist nicht sicher, dass $\underline{u} = (1, 0)$ tatsächlich gesendet wurde. |
| − | *Aber die Wahrscheinlichkeit ist angesichts des Empfangsvektors $\underline{y} = (1, 0, 1, 1, 1)$ hierfür am größten. | + | |
| + | *Aber die Wahrscheinlichkeit ist angesichts des Empfangsvektors $\underline{y} = (1, 0, 1, 1, 1)$ hierfür am größten. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 12. Juni 2022, 15:25 Uhr
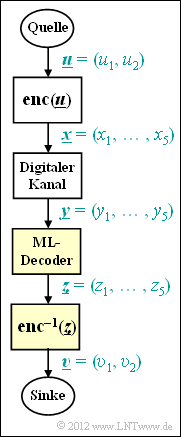
Wir betrachten das digitale Übertragungssystem entsprechend der Grafik. Berücksichtigt sind dabei:
- Ein systematischer $(5, 2)$–Blockcode $\mathcal{C}$ mit den Codeworten
- $$\underline{x}_{0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 0, 0, 0, 0) \hspace{0.05cm},$$ $$\underline{x}_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 1, 0, 1, 0) \hspace{0.05cm},$$ $$\underline{x}_{2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 0, 1, 0, 1) \hspace{0.05cm},$$ $$\underline{x}_{3} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 1, 1, 1, 1) \hspace{0.05cm};$$
- ein digitales (binäres) Kanalmodell, das den Vektor $\underline{x} \in {\rm GF} (2^{5})$ in den Vektor $\underline{y} \in {\rm GF} (2^{5})$ verfälscht;
- ein Maximum–Likelihood–Decoder (kurz: "ML–Decoder") mit der Entscheidungsregel
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}).$$
Hier bezeichnet $d_{\rm H} (\underline{y}, \ \underline{x_{i}})$ die Hamming–Distanz zwischen dem Empfangswort $\underline{y}$ und dem (möglicherweise) gesendeten Codewort $\underline{x_{i}}$.
Hinweis: Die Aufgabe gehört zum Kapitel "Kanalmodelle und Entscheiderstrukturen".
Fragebogen
Musterlösung
(1) Richtig ist die Antwort 3 ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$:
- Die Hamming–Distanzen zwischen dem spezifischen Empfangswort $\underline{y} = (1, 0, 0, 0, 1)$ und den vier möglichen Codeworten $\underline{x}_{i}$ ergeben sich wie folgt:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$
- Entschieden wird sich für die Folge mit der geringsten Hamming–Distanz $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$.
(2) Für $\underline{y} = (0, 0, 0, 1, 0)$ sind die Antworten 1 und 2 richtig, wie die folgende Rechnung zeigt:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$
(3) Richtig ist die Antwort 3:
- Entsprechend der Hamming–Distanz wäre eine Entscheidung zugunsten von $x_{2}$ genau so möglich wie für $x_{3}$, wenn $\underline{y} = (1, 0, 1, 1, 1)$ empfangen wird:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$
- Der Empfangsvektor $\underline{y}$ unterscheidet sich aber von $x_{2}$ bezüglich des vierten Bits und von $x_{3}$ im zweiten Bit.
- Da das vierte Bit unsicherer ist als das zweite, wird er sich für $x_{2}$ entscheiden .
(4) Da es sich hier um einen systematischen Code handelt, ist die Entscheidung für $\underline{z} = (1, 0, 1, 0, 1)$ gleichbedeutend mit der Entscheidung
- $$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$
- Es ist nicht sicher, dass $\underline{u} = (1, 0)$ tatsächlich gesendet wurde.
- Aber die Wahrscheinlichkeit ist angesichts des Empfangsvektors $\underline{y} = (1, 0, 1, 1, 1)$ hierfür am größten.