Aufgaben:Aufgabe 3.6Z: Prüfungskorrektur: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID148__Sto_Z_3_6.png|right|frame| | + | [[Datei:P_ID148__Sto_Z_3_6.png|right|frame|Tabelle für ${\rm \phi}(x)$ und ${\rm Q}(x)$]] |
| − | An einer Prüfung an der TU München haben $1000$ Studentinnen und Studenten teilgenommen. Ab der Note „4.0” gilt die Prüfung als bestanden. Die Prüfungsordnung sieht folgende Noten vor: | + | An einer Prüfung an der TU München haben $1000$ Studentinnen und Studenten teilgenommen. Ab der Note „4.0” gilt die Prüfung als bestanden. Die Prüfungsordnung sieht folgende Noten vor: |
:$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | :$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ | ||
Weiter ist bei der Aufgabe zu berücksichtigen: | Weiter ist bei der Aufgabe zu berücksichtigen: | ||
| − | *Die maximal erreichbare Punktzahl | + | *Die maximal erreichbare Punktzahl beträgt $100$. Der beste Student erreichte $88$ Punkte. |
| − | *Aufgrund der relativ großen Teilnehmerzahl ergibt sich für die erreichte Punktzahl – dies sei die Zufallsgröße $z$ – mit guter Näherung eine [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion|Gaußverteilung]] mit Mittelwert $m_z = 60$ und Streuung (Standardabweichung) $\sigma_z = 10$. | + | *Aufgrund der relativ großen Teilnehmerzahl ergibt sich für die erreichte Punktzahl – dies sei die Zufallsgröße $z$ – mit guter Näherung eine [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion|Gaußverteilung]] mit Mittelwert $m_z = 60$ und Streuung (Standardabweichung) $\sigma_z = 10$. |
| − | *Bei der Korrektur wurden nicht nur ganze | + | *Bei der Korrektur wurden nicht nur ganze Punktzahlen vergeben, sondern auch (beliebige) Zwischenwerte, so dass man die Zufallsgröße $z$ mit guter Näherung als „kontinuierlich” auffassen kann. |
Für die Bewertung werden als Richtlinien vorgegeben: | Für die Bewertung werden als Richtlinien vorgegeben: | ||
| − | *Auch mit sechs Punkten weniger als der Beste (ab $82$ Punkten) soll man „1.0” bekommen. | + | *Auch mit sechs Punkten weniger als der Beste $($also ab $82$ Punkten$)$ soll man „1.0” bekommen. |
| − | *Hat man $46\%$ der Gesamtpunktzahl erreicht, so hat man die Prüfung bestanden. | + | *Hat man $46\%$ der Gesamtpunktzahl erreicht, so hat man die Prüfung bestanden. |
*Die Punkte/Noten-Zuordnung soll linear erfolgen. | *Die Punkte/Noten-Zuordnung soll linear erfolgen. | ||
| Zeile 23: | Zeile 23: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilte Zufallsgrößen]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilte Zufallsgrößen]]. |
| − | *Gerade im Schulbereich wird die „Gaußverteilung” oft als „Normalverteilung” bezeichnet. Dies ist nicht ganz korrekt: | + | *Gerade im Schulbereich wird die „Gaußverteilung” oft als „Normalverteilung” bezeichnet. Dies ist nicht ganz korrekt: |
| − | *Eine normalverteilte Zufallsgröße $z$ hat zwar eine Gaußsche WDF und VTF, jedoch mit Mittelwert $m_z = 0$ und Streuung $\sigma_z = 1$. | + | *Eine normalverteilte Zufallsgröße $z$ hat zwar eine Gaußsche WDF und VTF, jedoch stets mit Mittelwert $m_z = 0$ und Streuung $\sigma_z = 1$. |
| Zeile 45: | Zeile 45: | ||
| − | {Wieviele Teilnehmer werden die Prüfung wohl nicht bestehen? | + | {Wieviele Teilnehmer werden die Prüfung wohl nicht bestehen? Berücksichtigen Sie, dass man $z$ als kontinuierliche Zufallsgröße auffassen kann. |
|type="{}"} | |type="{}"} | ||
$N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } | $N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } | ||
| − | {Legen Sie die Punkte/Noten–Zuordnung fest. Ab wann bekommt man eine „3.0“? | + | {Legen Sie die Punkte/Noten–Zuordnung fest. Ab wann bekommt man eine „3.0“? Wieviele Prüfungsteilnehmer werden diese Note erhalten? |
|type="{}"} | |type="{}"} | ||
$N_\text{3.0} \ = \ $ { 159 3% } | $N_\text{3.0} \ = \ $ { 159 3% } | ||
| − | {Wieviele Teilnehmer erhalten voraussichtlich die Note „2.7“? | + | {Wieviele Teilnehmer erhalten voraussichtlich die Note „2.7“? Begründen Sie, warum genau so viele Prüflinge die Note „3.3“ bekommen werden. |
|type="{}"} | |type="{}"} | ||
$N_\text{2.7} \ = \ $ { 146 3% } | $N_\text{2.7} \ = \ $ { 146 3% } | ||
| − | {Welche Mittelnote wird sich bei dieser Prüfung ergeben? | + | {Welche Mittelnote wird sich bei dieser Prüfung ergeben? Berücksichtigen Sie zur Lösung dieser Teilaufgabe das Ergebnis von Teilaufgabe '''(5)'''. |
|type="{}"} | |type="{}"} | ||
$\rm Mittelnote \ = \ $ { 3 3% } | $\rm Mittelnote \ = \ $ { 3 3% } | ||
Version vom 21. November 2019, 16:30 Uhr
An einer Prüfung an der TU München haben $1000$ Studentinnen und Studenten teilgenommen. Ab der Note „4.0” gilt die Prüfung als bestanden. Die Prüfungsordnung sieht folgende Noten vor:
- $$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$
Weiter ist bei der Aufgabe zu berücksichtigen:
- Die maximal erreichbare Punktzahl beträgt $100$. Der beste Student erreichte $88$ Punkte.
- Aufgrund der relativ großen Teilnehmerzahl ergibt sich für die erreichte Punktzahl – dies sei die Zufallsgröße $z$ – mit guter Näherung eine Gaußverteilung mit Mittelwert $m_z = 60$ und Streuung (Standardabweichung) $\sigma_z = 10$.
- Bei der Korrektur wurden nicht nur ganze Punktzahlen vergeben, sondern auch (beliebige) Zwischenwerte, so dass man die Zufallsgröße $z$ mit guter Näherung als „kontinuierlich” auffassen kann.
Für die Bewertung werden als Richtlinien vorgegeben:
- Auch mit sechs Punkten weniger als der Beste $($also ab $82$ Punkten$)$ soll man „1.0” bekommen.
- Hat man $46\%$ der Gesamtpunktzahl erreicht, so hat man die Prüfung bestanden.
- Die Punkte/Noten-Zuordnung soll linear erfolgen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Gaußverteilte Zufallsgrößen.
- Gerade im Schulbereich wird die „Gaußverteilung” oft als „Normalverteilung” bezeichnet. Dies ist nicht ganz korrekt:
- Eine normalverteilte Zufallsgröße $z$ hat zwar eine Gaußsche WDF und VTF, jedoch stets mit Mittelwert $m_z = 0$ und Streuung $\sigma_z = 1$.
Fragebogen
Musterlösung
- Nach dem zentralen Grenzwertsatz erhält man für die Summe vieler unabhängiger Größen eine Gaußverteilung.
- Im Umkehrschluss ergibt sich bei nur wenigen und dazu noch abhängigen Aufgaben keine Gaußverteilung.
- Eine einzige Ja/Nein-Frage führt zu einer Zweipunktverteilung (0 Punkte oder Maximalpunktzahl).
- Auch bei Einhaltung dieser Gebote wird man bei sehr wenigen Teilnehmern nicht mit einer „Normalverteilung” rechnen können.
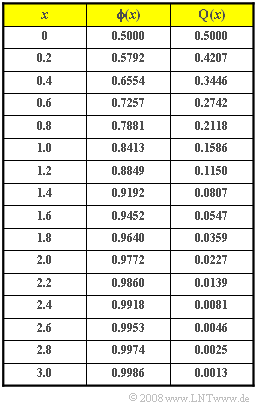
(2) Man bekommt eine „1.0” mit $82$ Punkten oder mehr. Deshalb gilt mit Mittelwert $m_z = 60$ und Streuung $\sigma_z = 10$:
- $$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$
Bei tausend Teilnehmern folgt daraus $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.
(3) Mit weniger als $46$ Punkten hat man die Prüfung nicht bestanden:
- $$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$
Also müssen wohl 81 Studenten nochmals antreten.
(4) Die Punktedifferenz $82 - 46 = 36$ muss auf neun Notenstufen (1.3, ... , 4.0) aufgeteilt werden.
- Jedes Intervall umfasst somit $4$ Punkte.
- Beispielsweise erhält man die Note „, wenn man $58$ bis $62$ Punkte erreicht.
- Die Wahrscheinlichkeit, dass die Punktzahl in diesem Bereich liegt, ergibt sich zu
- $$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$
Unter Ausnutzung der Symmetrie erhält man:
- $$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm Teilnehmer)}.$$
Anmerkungen:
- $z$ ist als kontinuierliche Zufallsgröße aufzufassen. Deshalb ist die Punktzahl $62$ gleichzeitig die obere Grenze für den „3.0”–Bereich als auch die untere Grenze für die Note „2.7” ist.
- Wäre $z$ nur ganzzahlig, so müsste $62$ je nach Stimmung des Korrektors entweder der Note „2.7” oder der Note „3.0” zugeordnet werden.
(5) Analog zur Musterlösung der Teilaufgabe (4) gilt für die Note „2.7”:
- $$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$
Aus Symmetriegründen erhält man für die Note „3.3” den gleichen Wert:
- $$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$
Also erhalten je 146 Teilnehmer die Note „2.7” bzw. „3.3”.
(6) Mit der hier getroffenen Punkte–Noten–Zuordnung sind nicht nur die Punkte um $m_z = 60$ symmetrisch verteilt, sondern auch die Noten um „3.0“. Es gibt
- genau so viele „2.7“ wie „3.3“ (um $±0.3$ von $3.0$ entfernt),
- genau so viele „2.3“ wie „3.7“ ($3.0 ±0.7$), und
- genau so viele „1.0“ wie „5.0“.
Deshalb ergibt sich die $\rm Mittelnote \hspace{0.15cm}\underline{ 3.0}$.