Aufgabe 2.5Z: Reichweite und Bitrate bei ADSL: Unterschied zwischen den Versionen
| Zeile 65: | Zeile 65: | ||
| − | {Welche Reichweite ergäbe sich aus der Faustformel für $R_{\rm ges} = 1 \ \rm Gbit/s$. | + | {Welche Reichweite ergäbe sich aus der angegebenen Faustformel für $R_{\rm ges} = 1 \ \rm Gbit/s$. |
|type="{}"} | |type="{}"} | ||
$l_{\rm max} \ = \ ${ 20 3% } $ \ m$ | $l_{\rm max} \ = \ ${ 20 3% } $ \ m$ | ||
| Zeile 71: | Zeile 71: | ||
{Berechnen Sie die charakteristischen Kabeldämpfungen für die Variante | {Berechnen Sie die charakteristischen Kabeldämpfungen für die Variante | ||
|type="{}"} | |type="{}"} | ||
| − | $\boldsymbol{\rm B:} \ | + | $\boldsymbol{\rm B}\text{:} \hspace{0.4cm} a_{\ast} \ = \ ${ 64.9 3% } $ \ \rm dB$ |
| − | $\boldsymbol{\rm C:} \ | + | $\boldsymbol{\rm C}\text{:} \hspace{0.4cm} a_{\ast} \ = \ ${ 48.2 3% } $ \ \rm dB$ |
| − | $\boldsymbol{\rm D:} \ | + | $\boldsymbol{\rm D}\text{:} \hspace{0.4cm}a_{\ast} \ = \ ${ 56 3% } $ \ \rm dB$ |
| − | $\boldsymbol{\rm E:} \ | + | $\boldsymbol{\rm E}\text{:} \hspace{0.4cm} a_{\ast} \ = \ ${ 40.7 3% } $ \ \rm dB$ |
</quiz> | </quiz> | ||
Version vom 14. Februar 2018, 17:15 Uhr
Die Entwicklung der xDSL–Technik begann 1995 mit dem ersten Standard für ADSL (Asymmetric Digital Subscriber Line). Ab 2006 kam in Deutschland auch das schnellere VDSL (Very High Data Rate Digital Subscriber Line) zum Einsatz.
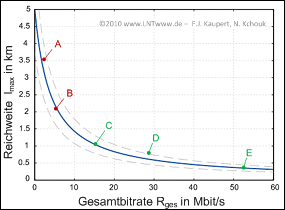
Die Grafik zeigt Fünf Systemvarianten in einem Diagramm, in dem die erreichbare Kabellänge $l_{\rm max}$ in Abhängigkeit der Gesamtbitrate $R_{\rm ges}$ aufgetragen ist:
- $\boldsymbol{\rm A}\text{:} \ \text{ Bitraten} \ 0.2 \ {\rm Mbit/s} + 2 \ {\rm Mbit/s}; \ \text{ Kabellänge } l_{\rm max} \approx 3.5 \ {\rm km},$
- $\boldsymbol{\rm B}\text{:} \ \text{ Bitraten} \ 0.2 \ {\rm Mbit/s} + 6 \ {\rm Mbit/s}; \ \text{ Kabellänge } l_{\rm max} \approx 2 \ {\rm km},$
- $\boldsymbol{\rm C}\text{:} \ \text{ Bitraten} \ 2 \ {\rm Mbit/s} + 13 \ {\rm Mbit/s}; \ \text{ Kabellänge } l_{\rm max} \approx 1 \ {\rm km},$
- $\boldsymbol{\rm D}\text{:} \ \text{ Bitraten} \ 2 \ {\rm Mbit/s} + 26 \ {\rm Mbit/s}; \ \text{ Kabellänge } \ l_{\rm max} \approx 0.8 \ {\rm km},$
- $\boldsymbol{\rm E}\text{:} \ \text{ Bitraten} \ 2 \ {\rm Mbit/s} + 51 \ {\rm Mbit/s}; \ \text{ Kabellänge } l_{\rm max} \approx 0.4 \ {\rm km}.$
Zu dieser Grafik ist weiter anzumerken:
- Alle Angaben gelten für eine Kupfer–Doppelader mit 0.4 mm Durchmesser.
- Eine der hier angegebenen Bitraten bezieht sich auf den Upstream, die andere auf den Downstream. Die Gesamtbitrate ist die Summe der beiden Anteile.
- Welche Bitrate sich auf den Upstream bezieht und welche auf den Downstream, wird in der Teilaufgabe (1) abgefragt.
- Die farbliche Unterscheidung der eingezeichneten Punkte bezieht sich auf die Unterteilung in ADSL und VDSL. Hierauf wird in der Teilaufgabe (2) Bezug genommen.
- Die blau eingezeichnete Kurve zeigt eine Faustformel, die den Zusammenhang zwischen Reichweite und Gesamtbitrate annähert:
- $$l_{\rm max}\,{\rm [in}\,\,{\rm km]} = \frac {20}{4 + R_{\rm ges}\,{\rm [in}\,\,{\rm Mbit/s]}} \hspace{0.05cm}.$$
- Gestrichelt eingezeichnet sind Abweichungen hiervon um $\pm 25\%$.
Häufig charakterisiert man ein leitungsgebundenes Übertragungssystem anhand der Kabeldämpfung bei der halben Bitrate (beachten Sie bitte das „a” bei der Dämpfung):
- $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R_{\rm B}}/{2}) = \alpha_{\rm K}(f = {R_{\rm B}}/{2}) \cdot l\hspace{0.05cm}.$$
Das Dämpfungsmaß (mit „alpha” notiert) ist für eine 0.4 mm Kupfer–Doppelader wie folgt gegeben:
- $$\alpha_{\rm K}(f ) = \left [ 5.1 + 14.3 \cdot \left ({f}/({\rm 1\,MHz})\right )^{0.59} \right ] {\rm dB}/{\rm km} \hspace{0.05cm}.$$
Für den Downlink von Variante $\boldsymbol{\rm A}$ mit $R_{\rm B} = 2 \ \rm Mbit/s$ ergibt sich somit mit $l = l_{\rm max} = 3.5 \ \rm km$:
- $$\alpha_{\rm K}(f = {\rm 1\,MHz}) = \left [ 5.1 + 14.3 \right ] {\rm dB}/{\rm km} = 19.4\,{\rm dB}/{\rm km}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm a}_{\rm \star} = 19.4\,{\rm dB}/{\rm km} \cdot 3.5\,{\rm km} = 67.9\,{\rm dB}\hspace{0.05cm}.$$
Die Werte für die anderen Systemvarianten sollen in der Teilaufgabe (4) ermittelt werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Verfahren zur Senkung der Bitfehlerrate bei DSL.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(2) Richtig ist der zweite Lösungsvorschlag. VDSL bietet höhere Bitraten an. Eine hohe Datenrate ist allerdings nur bei relativ kurzen Leitungslängen möglich.
(3) Die Reichweite eines solchen Gbit/s–Systems über Zweidrahtleitung wäre etwa $20/1000 \ {\rm km} \underline{= 20 \ \rm Meter}$. Betrachten Sie diese Teilaufgabe als akademisch.
(4) Hier ergeben sich folgende charakteristische Kabeldämpfungen. Für
- Variante $\boldsymbol{\rm B} \ (R_{\rm B}/2 = 3 {\rm \ Mbit/s}, \ l_{\rm max} = 2 {\rm \ km}):$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 3^{0.59} \right ] \cdot 2\,{\rm dB}\hspace{0.15cm}\underline{ \approx 64.9\,{\rm dB}}\hspace{0.05cm},$$
- Variante $\boldsymbol{\rm C} \ (R_{\rm B}/2 = 6.5 {\rm \ Mbit/s}, \ l_{\rm max} = 1 {\rm \ km}):$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 6.5^{0.59} \right ] \cdot 1\,{\rm dB} \hspace{0.15cm}\underline{\approx 48.2\,{\rm dB}}\hspace{0.05cm},$$
- Variante $\boldsymbol{\rm D} \ (R_{\rm B}/2 = 13 {\rm \ Mbit/s}, \ l_{\rm max} = 0.8 {\rm \ km}):$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 13^{0.59} \right ] \cdot 0.8\,{\rm dB}\hspace{0.15cm}\underline{ \approx 56\,{\rm dB}}\hspace{0.05cm},$$
- Variante $\boldsymbol{\rm E} \ (R_{\rm B}/2 = 25.5 {\rm \ Mbit/s}, \ l_{\rm max} = 0.4 {\rm \ km}):$
- $${\rm a}_{\rm \star} = \left [ 5.1 + 14.3 \cdot 25.5^{0.59} \right ] \cdot 0.4\,{\rm dB}\hspace{0.15cm}\underline{ \approx 40.7\,{\rm dB}}\hspace{0.05cm}.$$
Die charakteristische Kabeldämpfung $a_{\ast}$ von ADSL–Systemen liegt im Bereich $65 \ \rm dB ... 68 \ \rm dB$. Die VDSL–Varianten liefern charakteristische Kabeldämpfungen zwischen $40 \ \rm dB$ und $56 \ \rm dB$. Zu beachten ist allerdings, dass dieser bei herkömmlicher binärer Basisbandübertragung wichtige Systemparameter $a_{\ast}$ die Gegebenheiten bei OFDM bzw. Discrete Multitone Transmission nicht ausreichend gut wiedergibt.