Aufgaben:Aufgabe 4.4: Extrinsische L–Werte beim SPC: Unterschied zwischen den Versionen
| Zeile 80: | Zeile 80: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die Werte können aus der vierten Spalte der | + | Die Werte können aus der vierten Spalte der auf der Angabenseite beigefügten Tabelle abgelesen werden. |
| Zeile 90: | Zeile 90: | ||
:$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | :$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
(-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 | (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 97: | Zeile 97: | ||
:$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | :$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
(+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 | (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 105: | Zeile 105: | ||
:$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} | :$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} | ||
\right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} | \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} | ||
| − | \right ] | + | \right ]\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} | |
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| Zeile 114: | Zeile 114: | ||
= \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$ | = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$ | ||
| − | Multipliziert man Zähler und Nenner noch mit $\ | + | Multipliziert man Zähler und Nenner noch mit ${\rm e}^{-L_j/2}$, so erhält man: |
:$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$ | :$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$ | ||
| − | Somit sind <u>alle Lösungsvorschläge</u> richtig. Die Funktion <i>Tangens Hyperbolicus</i> findet man zum Beispiel tabellarisch in | + | Somit sind <u>alle Lösungsvorschläge</u> richtig. Die Funktion <i>Tangens Hyperbolicus</i> findet man zum Beispiel tabellarisch in Formelsammlungen oder in der letzten Spalte der vorne angegebenen Tabelle. |
| Zeile 123: | Zeile 123: | ||
:$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | :$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
(+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 | (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Zeile 133: | Zeile 133: | ||
Damit ergibt sich entsprechend der obigen [[Aufgaben:4.4_Extrinsische_L%E2%80%93Werte_beim_SPC|Tabelle]]: | Damit ergibt sich entsprechend der obigen [[Aufgaben:4.4_Extrinsische_L%E2%80%93Werte_beim_SPC|Tabelle]]: | ||
| − | :$$p_1 = 0.2 \hspace{0. | + | :$$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} |
| − | L_1 = +1.386 \hspace{0. | + | L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} |
| − | L_1/2 = +0.693 | + | L_1/2 = +0.693 \hspace{0.2cm} |
| − | + | \Rightarrow \hspace{0.2cm} | |
{\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} | {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} | ||
| − | = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm | + | = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$ |
| − | :$$p_2 = 0.9 \hspace{0. | + | :$$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} |
| − | L_2 = -2.197 \hspace{0. | + | L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} |
| − | L_2/2 = -1.099 | + | L_2/2 = -1.099\hspace{0.2cm} |
| − | + | \Rightarrow \hspace{0.2cm} | |
{\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} | {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} | ||
| − | = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm | + | = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$ |
| − | :$$p_3 = 0.3 \hspace{0. | + | :$$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} |
| − | L_3 = 0.847 \hspace{0. | + | L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} |
| − | L_3/2 = +0.419 | + | L_3/2 = +0.419 \hspace{0.2cm} |
| − | + | \Rightarrow \hspace{0.2cm} | |
{\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} | {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} | ||
| − | = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm | + | = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$ |
Das Endergebnis lautet somit: | Das Endergebnis lautet somit: | ||
Version vom 29. Januar 2018, 15:33 Uhr
Wir betrachten nochmals den Single Parity–check Code. Bei einem solchen SPC $(n, \, n-1, \, 2)$ stammen von den $n \ \rm Bits$ eines Codewortes $\underline{x}$ die ersten $k = n \, –1 \ \rm Bits$ von der Quellenfolge $\underline{u}$ und es wird nur ein einziges Prüfbit $p$ hinzugefügt, und zwar derart, dass die Anzahl der Einsen im Codewort geradzahlig ist:
- $$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Die extrinsische Information über das $i$–te Codebit wird über alle anderen Symbole $(j ≠ i)$ gebildet. Deshalb schreiben wir für das um ein Bit kürzere Codewort:
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Der extrinsische $L$–Wert über das $i$–te Codesymbol lautet mit dem Hamming–Gewicht $w_{\rm H}$ der verkürzten Folge $\underline{x}^{(-i)}$:
- $$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$
- Ist die Wahrscheinlichkeit im Zähler größer als die im Nenner, so ist $L_{\rm E}(i) > 0$ und damit wird auch der Aposteriori–$L$–Wert $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ vergrößert, das heißt tendenziell in Richtung des Symbols $x_i = 0$ beeinflusst.
- Bei $L_{\rm E}(i) < 0$ spricht aus Sicht der anderen Symbole $(j ≠ i)$ vieles dafür, dass $x_i = 1$ ist.
Behandelt wird ausschließlich der SPC (4, 3, 4), wobei für die Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ gilt:
- $$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} p_3 = 0.3 \hspace{0.05cm}, \hspace{0.3cm} p_4 = 0.6 \hspace{0.05cm}.$$
Daraus ergeben sich die Apriori–$L$–Werte zu:
- $$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} \right ] \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels Soft–in Soft–out Decoder
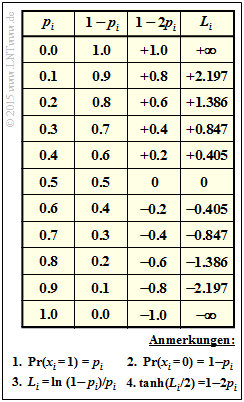
- In der oberen Tabelle sind für $p_i = 0$ bis $p_i = 1$ mit Schrittweite $0.1$ (Spalte 1) angegeben:
- In Spalte 2: die Wahrscheinlichkeit $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$,
- in Spalte 3: die Werte für $1 - 2p_i$,
- in Spalte 4: die Apriori–$L$–Werte $L_i = \ln {[(1 - p_i)/p_i]} = L_{\rm A}(i)$.
- Der Tangens Hyperbolicus ($\tanh$) von $L_i/2$ ist identisch mit $1-2p_i$ ⇒ Spalte 3.
- In der Aufgabe 4.4Z wird gezeigt, dass für den extrinsischen $L$–Wert auch geschrieben werden kann:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) \hspace{0.05cm}.$$
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} \hspace{0.05cm},$$
- $$L_{\rm A}(i = 2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_2}{p_2} \right ] = {\rm ln} \hspace{0.1cm} 1/9 \hspace{0.15cm}\underline{= -2.197} \hspace{0.05cm}.$$
Die Werte können aus der vierten Spalte der auf der Angabenseite beigefügten Tabelle abgelesen werden.
(2) Zur Berechnung des extrinsischen $L$–Wertes über das $i$–te Bit dürfen nur die Informationen über die drei anderen Bits $(j ≠ i)$ herangezogen werden. Mit der angegebenen Gleichung gilt:
- $$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} \hspace{0.05cm}.$$
Für das Produkt erhält man entsprechend der dritten Spalte der Tabelle:
- $$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} \hspace{0.05cm}.$$
Hinsichtlich Bit 2 erhält man entsprechend:
- $$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} \hspace{0.05cm}.$$
(3) Für den Apriori–$L$–Wert gilt:
- $$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } \hspace{0.05cm} .$$
Damit gilt auch:
- $$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$
Multipliziert man Zähler und Nenner noch mit ${\rm e}^{-L_j/2}$, so erhält man:
- $$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$
Somit sind alle Lösungsvorschläge richtig. Die Funktion Tangens Hyperbolicus findet man zum Beispiel tabellarisch in Formelsammlungen oder in der letzten Spalte der vorne angegebenen Tabelle.
(4) Wir berechnen $L_{\rm E}(i = 3)$ zunächst in gleicher Weise wie in der Teilaufgabe (2):
- $$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} \hspace{0.05cm}.$$
Den extrinsischen $L$–Wert hinsichtlich des letzten Bits berechnen wir nach der Gleichung
- $$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \hspace{0.05cm}.$$
Damit ergibt sich entsprechend der obigen Tabelle:
- $$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1/2 = +0.693 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$
- $$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2/2 = -1.099\hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$
- $$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3/2 = +0.419 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$
Das Endergebnis lautet somit:
- $$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 -0.192}{1 +0.192}\hspace{0.15cm}\underline{= -0.389} \hspace{0.05cm}.$$