Aufgabe 2.4: DSL/DMT mit IDFT/DFT: Unterschied zwischen den Versionen

Version vom 18. Dezember 2017, 14:01 Uhr

Zeitabtastwerte bei 3 verschiedenen DMT-Spektralbelegungen

Eine Realisierungsform des DMT–Verfahrens (steht für Discrete Multitone Transmission) basiert auf der Inversen Diskreten Fouriertransformation (IDFT) sowie der DFT am Empfänger.

Beim Sender werden $N/2–1$ Nutzer durch die komplexen Spektralkoeffizienten $D_{k} (k = 1, ..., N/2–1)$ den Frequenzen $f_{k} = k \cdot f_{0}$ zugewiesen, wobei die Grundfrequenz $f_{0}$ der Kehrwert der Symboldauer $T$ ist.

Es gilt $D_{k} \in {±1 ± j}$ , falls ein Kanal belegt ist, im anderen Fall $D_{k} = 0$ . Die Koeffizienten $D_{0}$ und $D_{N/2}$ sind stets 0. Die obersten Koeffizienten werden konjugiert–komplex belegt:

$D_k = D_{N-k}^{\star},\hspace{0.2cm}k = N/2 +1,\hspace{0.05cm} ... \hspace{0.05cm}, N-1 \hspace{0.05cm}.$

Fragebogen

Musterlösung

(1)

@@ Zeile 4: / Zeile 4: @@
 }}
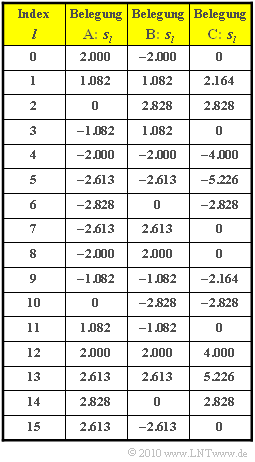
-[[Datei:|right|frame|]]
+[[Datei:P_ID1972__Bei_A_2_4.png|right|frame|Zeitabtastwerte bei 3 verschiedenen DMT-Spektralbelegungen]]
+Eine [[Beispiele_von_Nachrichtensystemen/xDSL_als_Übertragungstechnik#DMT.E2.80.93Realisierung_mit_IDFT.2FDFT|Realisierungsform]] des DMT–Verfahrens (steht für ''Discrete Multitone Transmission'') basiert auf der Inversen Diskreten Fouriertransformation (IDFT) sowie der DFT am Empfänger.
+Beim Sender werden  $N/2–1$  Nutzer durch die komplexen Spektralkoeffizienten  $D_{k} (k = 1, ..., N/2–1)$  den Frequenzen  $f_{k} = k \cdot f_{0}$  zugewiesen, wobei die Grundfrequenz  $f_{0}$  der Kehrwert der Symboldauer  $T$  ist.
+Es gilt  $D_{k} \in {±1 ± j}$ , falls ein Kanal belegt ist, im anderen Fall  $D_{k} = 0$ . Die Koeffizienten  $D_{0}$  und  $D_{N/2}$  sind stets 0. Die obersten Koeffizienten werden konjugiert–komplex belegt:
+: $D_k = D_{N-k}^{\star},\hspace{0.2cm}k = N/2 +1,\hspace{0.05cm} ... \hspace{0.05cm}, N-1 \hspace{0.05cm}.$