Aufgaben:Aufgabe 3.09: Grundlegendes zum Viterbi–Algorithmus: Unterschied zwischen den Versionen
Aus LNTwww
Wael (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Decodierung von Faltungscodes }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Fra…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Decodierung von Faltungscodes | + | {{quiz-Header|Buchseite=Kanalcodierung/Decodierung von Faltungscodes}} |
| + | [[Datei:P_ID2659__KC_A_3_8.png|right|frame|Zu analysierendes Trellis]] | ||
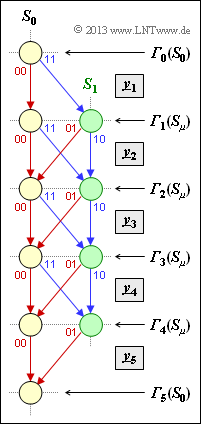
| + | Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und $\Gamma_i(S_1)$ zu den Zeitpunkten $i = 0$ bis $i = 5$. Aus diesem Trellis können zum Beispiel abgelesen werden: | ||
| + | * die Coderate $R$, | ||
| + | * das Gedächtnis $m$, | ||
| + | * die freie Distanz $d_{\rm F}$, | ||
| + | * die Informationssequenzlänge $L$, | ||
| + | * die Sequenzlänge $L'$ inklusive der Terminierung. | ||
| + | In der Aufgabe ist weiter zu klären: | ||
| + | * die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$, | ||
| + | * Auswirkungen von einem bzw. zwei Übertragungsfehlern. | ||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
| − | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Multiple-Choice | + | {Multiple-Choice |
|type="[]"} | |type="[]"} | ||
| − | + | + correct | |
| − | + | + | - false |
| − | |||
{Input-Box Frage | {Input-Box Frage | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $xyz \ = \ ${ 5.4 3% } $ab$ |
| − | |||
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' |
| − | '''2 | + | '''(2)''' |
| − | '''3 | + | '''(3)''' |
| − | '''4 | + | '''(4)''' |
| − | '''5 | + | '''(5)''' |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Kanalcodierung|^3.4 Decodierung von Faltungscodes | + | [[Category:Aufgaben zu Kanalcodierung|^3.4 Decodierung von Faltungscodes^]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ^]] | ||
Version vom 3. Dezember 2017, 20:53 Uhr
Die Grafik zeigt ein Trellisdiagramm und definiert gleichzeitig die Fehlergrößen ${\it \Gamma}_i(S_0)$ und $\Gamma_i(S_1)$ zu den Zeitpunkten $i = 0$ bis $i = 5$. Aus diesem Trellis können zum Beispiel abgelesen werden:
- die Coderate $R$,
- das Gedächtnis $m$,
- die freie Distanz $d_{\rm F}$,
- die Informationssequenzlänge $L$,
- die Sequenzlänge $L'$ inklusive der Terminierung.
In der Aufgabe ist weiter zu klären:
- die Bedeutung des Endwertes ${\it \Gamma}_5(S_0)$,
- Auswirkungen von einem bzw. zwei Übertragungsfehlern.
Hinweis:
- Die Aufgabe gehört zum Kapitel [[
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)