Aufgaben:Aufgabe 2.2: Binäre bipolare Rechtecke

• Zurück zum Buch

Beispiele für binäre bipolare Rechtecksignale

Wir gehen von folgendem Signal aus:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$

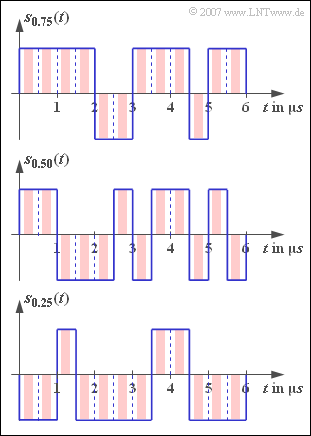
Der Sendegrundimpuls $g_{s}(t)$ wird in dieser Aufgabe stets als rechteckförmig angenommen, wobei das NRZ–Format (blaue Signalverläufe in der Grafik) als auch das RZ–Format mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ (rote Signalverläufe) zu untersuchen ist.

Die Amplitudenkoeffizienten besitzen die folgenden Eigenschaften:

• Sie sind binär und bipolar: $a_{\nu} \in \{–1, +1\}$.
• Die Symbole innerhalb der Folge $\langle a_{\nu }\rangle$ weisen keine statistischen Bindungen auf.
• Die Wahrscheinlichkeiten für die beiden möglichen Werte $±1$ lauten mit $0 < p < 1$:

$${\rm Pr}(a_\nu = +1) \ = \ p,$$

$${\rm Pr}(a_\nu = -1) \ = \ 1 - p \hspace{0.05cm}.$$

Die drei in der Grafik dargestellten Signalausschnitte gelten für $p = 0.75$, $p = 0.50$ und $p = 0.25$.

Im Laufe dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen:

• $m_{a} = \E[a_{\nu}]$ gibt den linearen Mittelwert der Amplitudenkoeffizienten an.
• $m_{2a} = \E[a_{\nu}^{2}]$ ist der quadratische Mittelwert.
• Damit kann auch die Varianz $\sigma_{a}^{2} = m_{2a} – m_{a}^{2}$ berechnet werden.
• Die diskrete AKF der Amplitudenkoeffizienten ist $\varphi_{a}(\lambda) = \E[a_{\nu} \cdot a_{\nu} + \lambda]$. Es gilt hier:

$$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 \\ m_1^2 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$$

• Die Energie–AKF des Sendegrundimpulses beträgt:

$$\varphi^{^{\bullet}}_{g_s}(\tau) = \left\{ \begin{array}{c} s_0^2 \cdot T_{\rm S} \cdot \left( 1 - {|\tau|}/{T_{\rm S}}\right) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}|\tau| \le T_{\rm S} \\ |\tau| \ge T_{\rm S} \hspace{0.05cm}.\\ \end{array}$$

• Damit erhält man für die gesamte AKF des Sendesignals:

$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{g_s}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$

• Das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ ist die Fouriertransformierte der AKF $\varphi_{s}(\tau)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Grundlagen der codierten Übertragung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der drei dargestellten Signale sind redundanzfrei?

	$s_{0.75}(t)$,
	$s_{0.50}(t)$,
	$s_{0.25}(t)$,

2

Wie groß ist der quadratische Mittelwert $m_{2a}$ der Amplitudenkoeffizienten in Abhängigkeit von $p$?

$p = 0.75\text{:} \hspace{0.4cm} m_{2a} \ = \ $

$p = 0.50\text{:} \hspace{0.4cm} m_{2a} \ = \ $

$p = 0.25\text{:} \hspace{0.4cm} m_{2a} \ = \ $

3

Berechnen Sie den linearen Mittelwert $m_{a}$ in Abhängigkeit von $p$.

$p = 0.75\text{:} \hspace{0.4cm} m_{a} \ = \ $

$p = 0.50\text{:} \hspace{0.4cm} m_{a} \ = \ $

$p = 0.25\text{:} \hspace{0.4cm} m_{a} \ = \ $

4

Wie groß ist die Varianz $\sigma_{a}^{2}$ der Amplitudenkoeffizienten?

$p = 0.75\text{:} \hspace{0.4cm} \sigma_{a}^{2} \ = \ $

$p = 0.50\text{:} \hspace{0.4cm} \sigma_{a}^{2} \ = \ $

$p = 0.25\text{:} \hspace{0.4cm} \sigma_{a}^{2} \ = \ $

5

Es gelte zunächst $p = 0.5$. Skizzieren Sie die AKF $\varphi_{s}(\tau)$ für den NRZ– und den RZ–Grundimpuls und bewerten Sie folgende Aussagen:

	Die AKF ist in beiden Fällen dreieckförmig.
	Das LDS verläuft in beiden Fällen ${\rm si}^{2}$–förmig.
	Die LDS–Fläche ist in beiden Fällen gleich.
	Bei RZ–Impulsen beinhaltet ${\it \Phi}_{s}(f)$ zusätzliche Diracfunktionen.

6

Es gelte nun $p = 0.75$. Skizzieren Sie die AKF für den NRZ–Grundimpuls und bewerten Sie folgende Aussagen:

	Die AKF besteht aus einem Dreieck und einem Gleichanteil.
	Das LDS besteht aus einem ${\rm si}^{2}$–Anteil und einem Dirac.
	Die Diracfunktion hat das Gewicht $s_{0}^{2}$.
	Mit $p = 0.25$ ergibt sich das gleiche Leistungsdichtespektrum.

7

Es gelte weiter $p = 0.75$. Skizzieren Sie die AKF für den RZ–Grundimpuls und bewerten Sie folgende

	Auch hier beinhaltet das LDS einen ${\rm si}^{2}$–förmigen Anteil.
	Gleichzeitig gibt es im LDS noch unendlich viele Diraclinien.

Musterlösung

Musterlösung

(1)  Man spricht von einem redundanzfreien Digitalsignal, wenn

• die Amplitudenkoeffizienten nicht voneinander abhängen (dies wurde hier vorausgesetzt),
• alle möglichen Amplitudenkoeffizienten gleichwahrscheinlich sind.

In diesem Sinne ist $s_{0.5}(t)$ ein redundanzfreies Signal $\Rightarrow$ Lösungsvorschlag 2. Somit ist hier die Entropie (der mittlere Informationsgehalt pro übertragenem Binärsymbol) maximal gleich dem Entscheidungsgehalt:

$$H_{\rm max} = {1}/{2}\cdot {\rm log}_2 (2)+{1}/{2}\cdot {\rm log}_2 (2) = 1 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$

Dagegen gilt für die Entropien der beiden anderen Binärsignale:

$$H = \ \frac{3}{4}\cdot {\rm log}_2 (\frac{4}{3})+ \frac{1}{4}\cdot {\rm log}_2 (4) = \left( \frac{3}{4} + \frac{1}{4}\right)\cdot {\rm log}_2 (4) - \frac{3}{4}\cdot{\rm log}_2 (3) =$$

$$ \hspace{0.5cm} = \ 2 - \frac{3}{4}\cdot{\rm log}_2 (3) = 0.811 \,\,{\rm bit/Bin\ddot{a}rsymbol} \hspace{0.05cm}.$$

Daraus ergibt sich für die relative Redundanz dieser Signale:

$$r = \frac{H_{\rm max} - H}{H_{\rm max}}\hspace{0.15cm} \approx 18.9\%\hspace{0.05cm}.$$

(2)  Der quadratische Mittelwert ist unabhängig von $p$ gleich $m_{2a} = 1$:

$$m_{2a}={\rm E}[a_\nu^2] = p \cdot (+1)^2 + (1-p)\cdot (-1)^2 \hspace{0.15cm}\underline { = 1 \hspace{0.05cm}}.$$

(3)  Für den linearen Mittelwert erhält man

$$m_{a}={\rm E}[a_\nu] = p \cdot (+1) + (1-p)\cdot (-1) = 2 p -1 \hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm} p = 0.75: m_{a}\hspace{0.15cm}\underline {=0.50},\hspace{0.2cm} p = 0.50: m_{a}\hspace{0.15cm}\underline {=0},\hspace{0.2cm} p = 0.25: m_{a}\hspace{0.15cm}\underline { =-0.50 \hspace{0.05cm}}.$$

(4)  Mit den Ergebnissen aus (2) und (4) erhält man:

$$p \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.75 \hspace{-0.05cm}: \hspace{0.15cm} \sigma_{a}^2 \hspace{0.15cm}\underline {=0.75},$$

$$ p \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.50 \hspace{-0.05cm}:\hspace{0.15cm} \sigma_{a}^2\hspace{0.15cm} \underline { =1.00 \hspace{0.05cm}},$$

$$ p \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.25 \hspace{-0.05cm}: \hspace{0.15cm} \sigma_{a}^2 \hspace{0.15cm}\underline {=0.75}.$$

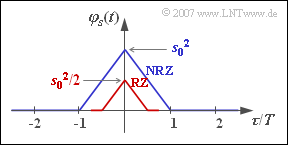
(5)  Für $p = 0.5$ gilt $\varphi_{a}(\lambda = 0) = 1$ und $\varphi_{a}(\lambda \neq 0) = 0$. Daraus folgt:

$$\varphi_s(\tau) = \frac{1}{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau )\hspace{0.05cm}.$$

AKF bei gleichwahrscheinlichen Symbolen

Damit ergeben sich sowohl beim NRZ– als auch beim RZ–Grundimpuls eine dreieckförmige AKF und ein ${\rm si}^{2}$–förmiges LDS. Die Fläche unter dem LDS ist beim RZ–Impuls um den Faktor $T_{\rm S}/T$ kleiner als beim NRZ–Impuls, da sich auch die AKF–Werte bei $\tau = 0$ um diesen Faktor unterscheiden. Das LDS ist in beiden Fällen kontinuierlich, da die AKF keinen Gleichanteil und keine periodischen Anteile beinhaltet.

Richtig sind also nur die beiden ersten Aussagen.

AKF bei ungleichen Symbolwahrscheinlichkeiten

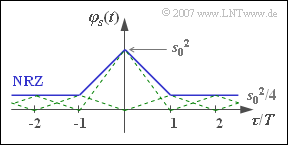
(6)  Für $p = 0.75$ setzt sich die AKF $\varphi_{s}(\tau)$ aus unendlich vielen Dreieckfunktionen zusammen, die mit Ausnahme des mittleren Dreiecks um $\tau = 0$ alle die gleiche Höhe $s_{0}^{2}/4$ aufweisen. Entsprechend der Skizze kann man alle diese Dreieckfunktionen zu einem Gleichanteil der Höhe $m_{a}^{2} \cdot s_{0}^{2} = s_{0}^{2}/4$ und einem einzigen Dreieck um $\tau = 0$ mit der Höhe $\sigma_{a}^{2} \cdot s_{0}^{2} = 3/4 · s_{0}^{2}$ zusammenfassen.

Im LDS führt dies zu einem kontinuierlichen, ${\rm si}^{2}$–förmigem Anteil und zu einer Diracfunktion bei $f = 0$. Das Gewicht dieses Diracs ist $s_{0}^{2}/4$. Für $p = 0.25$ ergibt sich die gleiche AKF wie mit $p = 0.75$, da sowohl der quadratische Mittelwert $m_{2a} = 1$ als auch $m_{a}^{2} = 0.25$ übereinstimmen. Somit stimmen natürlich auch die Leistungsdichtespektren überein.

Richtig sind somit alle Aussagen mit Ausnahme der dritten.

AKF bei RZ-Rechteckimpulsen

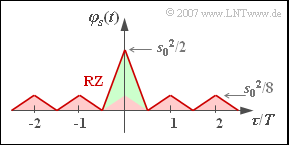
(7)  Mit dem RZ–Tastverhältnis $T_{\rm S}/T = 0.5$ ergibt sich die skizzierte AKF, die auch durch eine periodische Dreieckfunktion der Höhe $s_{0}^{2}/8$ (mit roter Füllung) und einem einzigen Dreieckimpuls der Höhe $3/8 \cdot s_{0}^{2}$ (grün gefüllt) dargestellt werden kann. Dieser nichtperiodische Anteil führt zu einem kontinuierlichen, ${\rm si}^{2}$–förmigen LDS mit Nullstellen bei Vielfachen von $2/T$.

Das periodische Dreiecksignal bewirkt Diracfunktionen bei Vielfachen von $1/T$. Aufgrund der Antimetrie des periodischen Anteils besitzen die Diracfunktionen bei Vielfachen von $2/T$ jeweils das Gewicht $0$. Die Gewichte der Diracfunktionen im Abstand $1/T$ sind proportional zum kontinuierlichen LDS–Anteil.

Beide Lösungsvorschläge sind somit richtig.