Aufgaben:Aufgabe 2.7Z: Leistungsdichtespektren der Pseudoternärcodes

• Zurück zum Buch

Leistungsdichtespektren der Pseudoternärcodes

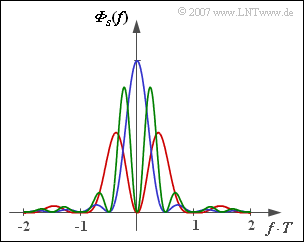
In der Grafik sehen Sie die Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes, die sich aus der allgemeinen Beschreibung gemäß Aufgabe A2.7 durch unterschiedliche Werte der Parameter $N_{\rm C}$ und $K_{\rm C}$ ergeben. In verschiedenen Farben sind die Leistungsdichtespektren

$${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \left [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\right ]$$

für folgende Varianten dargestellt:

• AMI–Code $(N_{\rm C} = 1, K_{\rm C} = +1)$,
• Duobinärcode $(N_{\rm C} = 1, K_{\rm C} = –1)$,
• Bipolarcode zweiter Ordnung $(N_{\rm C} = 2, K_{\rm C} = +1)$.

Bei obiger LDS–Gleichung ist die Verwendung von rechteckförmigen NRZ–Sendegrundimpulsen vorausgesetzt. Alle hier betrachteten Pseudoternärcodes besitzen dieselbe Wahrscheinlichkeitsverteilung:

$${\rm Pr}[s(t) = 0]= {1}/{2},\hspace{0.2cm}{\rm Pr}[s(t) = +s_0]= {\rm Pr}[s(t) = -s_0]={1}/{4}\hspace{0.05cm}.$$

Hinweis:

Die Aufgabe gehört zum Symbolweise Codierung mit Pseudoternärcodes. Sie können Ihre Ergebnisse mit folgendem Interaktionsmodul überprüfen: Signale, AKF und LDS der Pseutoternärcodes

Fragebogen

1

Welcher Kurvenzug gehört zum AMI–Code?

	rot,
	blau,
	grün.

2

Welcher Kurvenzug gehört zum Duobinärcode?

	rot,
	blau,
	grün.

3

Welcher Kurvenzug gehört zum Bipolarcode zweiter Ordnung?

	rot,
	blau,
	grün.

4

Welcher Code besitzt die größte Sendeleistung?|type="[]"

	AMI–Code.
	Duobinärcode.
	Bipolarcode 2. Ordnung.
	Die Sendeleistung ist bei allen Codes gleich.

5

Welcher dieser Codes ist gleichsignalfrei?

	AMI–Code.
	Duobinärcode.
	Bipolarcode 2. Ordnung.

6

Warum benötigt man beim „Telefonkanal” gleichsignalfreie Codes?

	Zur Verbindung von Leitungen unterschiedlicher Impedanz braucht man Übertrager. Diese haben Hochpasscharakter.
	Da die Stromversorgung oft über die Signalleitung erfolgt, darf das Nachrichtensignal keinen Gleichsignalanteil beinhalten.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)  (6)