Aufgaben:Aufgabe 4.2: AM/PM-Schwingungen: Unterschied zwischen den Versionen
| Zeile 54: | Zeile 54: | ||
{Wie lautet die Basisfunktion $\varphi_1(t)$ nach Gram–Schmidt? | {Wie lautet die Basisfunktion $\varphi_1(t)$ nach Gram–Schmidt? | ||
|type="[]"} | |type="[]"} | ||
| − | - $\varphi_1(t) = E^{\rm 0.5} \cdot cos(2\pi f_{\rm T}t)$, | + | - $\varphi_1(t) = E^{\rm 0.5} \cdot {\rm cos}(2\pi f_{\rm T}t)$, |
- $\varphi_1(t) = cos(2\pi f_{\rm T}t)$, | - $\varphi_1(t) = cos(2\pi f_{\rm T}t)$, | ||
| − | + $\varphi_1(t) = (2/T)^{\rm 0.5} \cdot cos(2\pi f_{\rm T}t)$. | + | + $\varphi_1(t) = (2/T)^{\rm 0.5} \cdot {\rm cos}(2\pi f_{\rm T}t)$. |
{Welcher Zusammenhang besteht zwischen $s_1(t)$ und $\varphi_1(t)$? | {Welcher Zusammenhang besteht zwischen $s_1(t)$ und $\varphi_1(t)$? | ||
| Zeile 70: | Zeile 70: | ||
{Wie lautet die Hilfsfunktion $\theta_2(t)$? | {Wie lautet die Hilfsfunktion $\theta_2(t)$? | ||
|type="[]"} | |type="[]"} | ||
| − | - $\theta_2(t) = +2^{\rm 0.5} \cdot A \cdot sin(2\pi f_{\rm T}t)$, | + | - $\theta_2(t) = +2^{\rm 0.5} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$, |
| − | + $\theta_2(t) = –2^{\rm 0.5} \cdot A \cdot sin(2\pi f_{\rm T}t)$, | + | + $\theta_2(t) = –2^{\rm 0.5} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$, |
| − | - $\theta_2(t) = (2/T)^{\rm 0.5} \cdot sin(2\pi f_{\rm T}t)$. | + | - $\theta_2(t) = (2/T)^{\rm 0.5} \cdot {\rm sin}(2\pi f_{\rm T}t)$. |
{Gegen Sie die Koeffizienten von $s_2(t) = s_{\rm 21} \cdot \varphi_1(t) + s_{\rm 22} \cdot \varphi_2(t)$ an. | {Gegen Sie die Koeffizienten von $s_2(t) = s_{\rm 21} \cdot \varphi_1(t) + s_{\rm 22} \cdot \varphi_2(t)$ an. | ||
Version vom 4. November 2017, 10:23 Uhr
Wir betrachten verschiedene Signalmengen $\{s_i(t)\}$ mit der Laufvariablen $i = 1, \ ... \, M$, die alle in gleicher Weise dargestellt werden können:
- $$s_i(t) = \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
Die Signaldauer $T$ ist dabei ein ganzzahliges Vielfaches von $1/f_{\rm T}$, wobei $1/f_{\rm T}$ die Signalfrequenz (Trägerfrequenz) angibt.
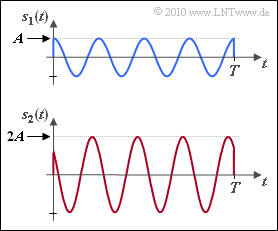
Für die Skizze beträgt die Dauer der energiebegrenzten Signale jeweils $T = 4/f_{\rm T}$, das heißt, man erkennt jeweils genau vier Schwingungen innerhalb von $T$. Die einzelnen Signale $s_i(t)$ unterscheiden sich in der Amplitude ($A_i$) und/oder der Phase ($\phi_i$). Für die beiden ersten (in der Grafik dargestellten) Signale gilt:
- $$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$
Beschränkt man sich zunächst auf diese beiden Signale $s_1(t)$ und $s_2(t)$, so kann man diese durch die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ vollständig beschreiben. Diese sind orthonormal zueinander, das heißt, unter Berücksichtigung der Zeitbegrenzung auf $T$ gilt:
- $$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm}, \hspace{0.2cm} \int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 \hspace{0.05cm}.$$
Mit diesen Basisfunktionen lassen sich die beiden Signale wie folgt darstellen:
- $$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) \hspace{0.05cm},$$
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$
In der Teilaufgabe (7) soll überprüft werden, ob sich alle Signale $s_i(t)$ gemäß der obigen Definition (mit beliebiger Amplitude $A_i$ und beliebiger Phase $\phi_i$) durch die folgende Gleichung beschreiben lassen:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$
Die Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sollen hier durch das Gram–Schmidt–Verfahren gefunden werden, das im Theorieteil ausführlich beschrieben wurde. Die erforderlichen Gleichungen sind hier nochmals zusammengestellt:
- $$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} \hspace{0.05cm},$$
- $$s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}s_2(t) \cdot \varphi_1(t)\, {\rm d} t \hspace{0.05cm},$$
- $$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm}, \hspace{0.2cm} \varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Kapitel Signale, Basisfunktionen und Vektorräume.
- Verwenden Sie zur Abkürzung die Energie $E = 1/2 \cdot A^2 \cdot T$.
- Desweiteren ist die folgende trigonometrische Beziehung gegeben:
- $$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$
Fragebogen
Musterlösung