Aufgaben:Aufgabe 1.7: Nahezu kausaler Gaußtiefpass: Unterschied zwischen den Versionen
| Zeile 32: | Zeile 32: | ||
| − | {Es gelte $x(t) = 1 {\rm V} · \cos(2π · 6 {\rm MHz }· t)$. Wie lautet das Ausgangssignal $y(t)$? Welcher Signalwert ergibt sich zur Zeit $t = 0$? | + | {Es gelte $x(t) = 1 {\rm V} · \cos(2π · 6\ {\rm MHz }· t)$. Wie lautet das Ausgangssignal $y(t)$? Welcher Signalwert ergibt sich zur Zeit $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y(t = 0) \ =$ { -0.175--0.165 } $\ \rm V$ | $y(t = 0) \ =$ { -0.175--0.165 } $\ \rm V$ | ||
| − | {Eigentlich sollte bei Kausalität $h(t < 0) = 0$ gelten. Wie groß ist der maximale relative Fehler des betrachteten Modells? Definition siehe Angabenseite. | + | {Eigentlich sollte bei Kausalität $h(t < 0) = 0$ gelten. Wie groß ist der maximale relative Fehler $\varepsilon_{\rm max}$ des betrachteten Modells? Definition siehe Angabenseite. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varepsilon_{\rm max} \ =$ { 3.49 5% } $\ \cdot 10^{-6}$ |
| Zeile 51: | Zeile 51: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
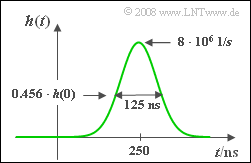
| − | + | '''(1)''' Die äquivalente Bandbreite $Δf$ ist gleich $h(t = τ) \ \rm \underline{= \ 8 \ MHz}$. Dies ist gleichzeitig der Kehrwert der äquivalenten Impulsdauer $Δt = 125 \ \rm ns$. Auch die Phasenlaufzeit $τ \ \rm \underline{= \ 250 \ \rm ns}$ kann direkt aus der Grafik abgelesen werden. | |
| − | + | '''(2)''' Ohne Berücksichtigung der Laufzeit ergäbe sich ein Cosinussignal mit der Amplitude | |
$$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$ | $$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$ | ||
| − | + | Die Laufzeit bewirkt eine Phasenverschiebung um $3π$: | |
$$\begin{align*} y(t) & = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) \\ & = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).\end{align*}$$ | $$\begin{align*} y(t) & = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) \\ & = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).\end{align*}$$ | ||
| − | + | Der gesuchte Wert ist somit $y(t = 0) \ \rm \underline{= \ –0.171 \ V}$. | |
| − | + | '''(3)''' Die Impulsantwort lautet: | |
$$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$ | $$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$ | ||
| − | + | Da $h(t)$ im Bereich $t < 0$ stetig zunimmt, tritt der Maximalwert (bei negativen Zeiten) etwa bei $t = 0$ auf: | |
$$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$ | $$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$ | ||
| − | + | Mit $h(t = τ) = Δf$ erhält man so: | |
| − | $$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49 \cdot 10^{-6 | + | $$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49} \cdot 10^{-6} .$$ |
| − | + | '''(4)''' Wir lassen vorerst die Phasenlaufzeit $τ$ des zweiten Systems außer Betracht und berechnen die Sprungantwort des Gaußtiefpasses: | |
| − | $$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \ | + | $$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$$ |
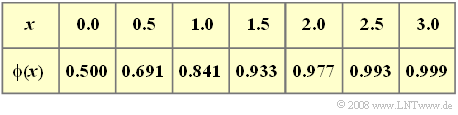
| − | + | Nach der Substitution $t ' → u$ sowie mit dem Gaußschen Fehlerintegral $ϕ(x)$ erhält man | |
| − | $$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \ | + | $$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),$$ |
$${\rm nach\hspace{0.15cm} Substitution\hspace{-0.15cm}:}\hspace{0.3cm}u = \frac{\sqrt{2\pi}}{\Delta t} \cdot t' , \hspace{0.3cm}{\rm wobei} \hspace{0.15cm}\hspace{0.2cm} | $${\rm nach\hspace{0.15cm} Substitution\hspace{-0.15cm}:}\hspace{0.3cm}u = \frac{\sqrt{2\pi}}{\Delta t} \cdot t' , \hspace{0.3cm}{\rm wobei} \hspace{0.15cm}\hspace{0.2cm} | ||
{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | {\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot | ||
| − | \ | + | \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$ |
| − | + | Unter Berücksichtigung der Laufzeit $τ$ erhält man für die gesamte Sprungantwort: | |
$$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$ | $$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$ | ||
| − | + | Der Wert bei $t = τ = 250 \ \rm ns$ ergibt sich zu $\ \rm \underline{ϕ(0) \ = \ 0.500}$. Entsprechend erhält man für $t = τ = 300 \ \rm ns$: | |
$$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$ | $$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$ | ||
Version vom 30. Januar 2017, 11:00 Uhr
Messungen haben ergeben, dass ein LZI–System mit guter Näherung durch einen Gaußtiefpass angenähert werden kann, wenn man eine zusätzliche Laufzeit $τ$ berücksichtigt. Somit lautet der Frequenzgang:
$$H(f) = {\rm e}^{-\pi(f/\Delta f)^2} \cdot {\rm e}^{-{\rm j}2\pi f \tau}.$$ Die beiden Systemparameter $Δt = 1/Δf$ und $τ$ können der in der Grafik dargestellten Impulsantwort $h(t)$ entnommen werden.
Es ist offensichtlich, dass dieses Modell nicht exakt der Wirklichkeit entspricht, da die Impulsantwort $h(t)$ auch für $t < 0$ nicht vollkommen verschwindet. In der Teilaufgabe (3) wird deshalb nach dem maximalen relativen Fehler gefragt, der wie folgt definiert ist: $$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< \hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$$ In Worten: Der maximale relative Fehler $ε_{\rm max}$ ist gleich dem Maximalwert der Impulsantwort $h(t)$ bei negativen Zeiten, bezogen auf den maximalen Wert $h(t = τ)$ der Impulsantwort.
Hinweise:
- Die Aufgabe gehört bezieht sich auf die Seite Gaußtiefpass .
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Zur Berechnung von Sprung– und Rechteckantwort können Sie das Gaußsche Fehlerintegral verwenden:
$${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int\limits_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
Fragebogen
Musterlösung
(2) Ohne Berücksichtigung der Laufzeit ergäbe sich ein Cosinussignal mit der Amplitude
$$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$$
Die Laufzeit bewirkt eine Phasenverschiebung um $3π$:
$$\begin{align*} y(t) & = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) \\ & = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).\end{align*}$$
Der gesuchte Wert ist somit $y(t = 0) \ \rm \underline{= \ –0.171 \ V}$.
(3) Die Impulsantwort lautet:
$$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$$
Da $h(t)$ im Bereich $t < 0$ stetig zunimmt, tritt der Maximalwert (bei negativen Zeiten) etwa bei $t = 0$ auf:
$$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$$
Mit $h(t = τ) = Δf$ erhält man so:
$$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49} \cdot 10^{-6} .$$
(4) Wir lassen vorerst die Phasenlaufzeit $τ$ des zweiten Systems außer Betracht und berechnen die Sprungantwort des Gaußtiefpasses:
$$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$$
Nach der Substitution $t ' → u$ sowie mit dem Gaußschen Fehlerintegral $ϕ(x)$ erhält man
$$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),$$
$${\rm nach\hspace{0.15cm} Substitution\hspace{-0.15cm}:}\hspace{0.3cm}u = \frac{\sqrt{2\pi}}{\Delta t} \cdot t' , \hspace{0.3cm}{\rm wobei} \hspace{0.15cm}\hspace{0.2cm}
{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot
\int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
Unter Berücksichtigung der Laufzeit $τ$ erhält man für die gesamte Sprungantwort:
$$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$$
Der Wert bei $t = τ = 250 \ \rm ns$ ergibt sich zu $\ \rm \underline{ϕ(0) \ = \ 0.500}$. Entsprechend erhält man für $t = τ = 300 \ \rm ns$:
$$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$$