Mobile Kommunikation/Statistische Bindungen innerhalb des Rayleigh-Prozesses: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
|||
| Zeile 60: | Zeile 60: | ||
Die LDS–Variable ist die [http://www.lntwww.de/Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Dopplerfrequenz_und_deren_Verteilung_.281.29 Dopplerfrequenz] <i>f</i><sub>D</sub>, da beim Mobilfunk der <i>Dopplereffekt</i> die Ursache der statistischen Bindungen ist. Dieser Effekt wird auf der nächsten Seite erläutert. | Die LDS–Variable ist die [http://www.lntwww.de/Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Dopplerfrequenz_und_deren_Verteilung_.281.29 Dopplerfrequenz] <i>f</i><sub>D</sub>, da beim Mobilfunk der <i>Dopplereffekt</i> die Ursache der statistischen Bindungen ist. Dieser Effekt wird auf der nächsten Seite erläutert. | ||
| − | == Phänomenologische Beschreibung des Dopplereffektes | + | == Phänomenologische Beschreibung des Dopplereffektes== |
<br> | <br> | ||
Die statistischen Bindungen innerhalb der reellen „Signale” <i>x</i>(<i>t</i>) und <i>y</i>(<i>t</i>) bzw. innerhalb der komplexen Größe <i>z</i>(<i>t</i>) sind auf den Dopplereffekt zurückzuführen. Dieser wurde Mitte des 19. Jahrhunderts von dem österreichischen Mathematiker, Physiker und Astronomen Christian Andreas Doppler theoretisch vorhergesagt und nach ihm benannt.<br> | Die statistischen Bindungen innerhalb der reellen „Signale” <i>x</i>(<i>t</i>) und <i>y</i>(<i>t</i>) bzw. innerhalb der komplexen Größe <i>z</i>(<i>t</i>) sind auf den Dopplereffekt zurückzuführen. Dieser wurde Mitte des 19. Jahrhunderts von dem österreichischen Mathematiker, Physiker und Astronomen Christian Andreas Doppler theoretisch vorhergesagt und nach ihm benannt.<br> | ||
Version vom 11. Oktober 2017, 10:06 Uhr
Inhaltsverzeichnis
Einige allgemeine Bemerkungen zu AKF und LDS
Zur Beschreibung der inneren statistischen Bindungen zwischen den benachbarten Signalwerten r(t) und r(t + Δt) eignet sich die Autokorrelationsfunktion (AKF):
\[\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\left [ r(t) \cdot r^{\star}(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.\]
Gegenüber der Definition unter obigem Link sind folgende Unterschiede zu erkennen:
- Die AKF–Variable ist hier mit Δt anstelle von τ bezeichnet, da wir in diesem Buch das „τ” noch für die 2D–Impulsantwort h(t, τ) benötigen.
- Das äquivalente Tiefpass–Signal r(t) ist komplex. Durch den Faktor 1/2 bezieht sich aber die AKF φr(Δt) und insbesondere die Leistung φr(Δt = 0) auf das Bandpass–Signal rBP(t).
Beim Rayleigh–Fading–Kanalmodell gilt r(t) = s(t) · z(t). Damit ergibt sich für dessen AKF:
\[\varphi_r ({\rm \Delta}t) = {1}/{2} \cdot {\rm E}\left [ s(t) \cdot z(t) \cdot s^{\star}(t + {\rm \Delta}t) \cdot z^{\star}(t + {\rm \Delta}t)\right ] = \varphi_s ({\rm \Delta}t) \cdot \varphi_z ({\rm \Delta}t)\hspace{0.05cm}.\]
Für die AKF von Sendesignal s(t) und multiplikativem Faktor z(t) gelten folgende Definitionen:
\[ \varphi_s ({\rm \Delta}t) \hspace{-0.1cm} = \hspace{-0.1cm} {1}/{2} \cdot {\rm E}\left [ s(t) \cdot s^{\star}(t + {\rm \Delta}t)\right ] \hspace{0.05cm},\] \[\varphi_z ({\rm \Delta}t) \hspace{-0.1cm} = \hspace{-0.1cm} {\rm E}\left [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\right ]\hspace{0.05cm}.\]
Der Faktor 1/2 ist nur bei der AKF–Berechnung von BP–Signalen im äquivalenten TP–Bereich zu berücksichtigen, nicht jedoch bei φz(Δt). Ansonsten würde sich φr(Δt) ≠ φs(Δt) · φz(Δt) ergeben.
Aufgrund der Definition φz(Δt) = E[z(t) · z*(t + Δt)] ist die AKF auch bei einer komplexen Zeitfunktion z(t) stets reell und zudem bezüglich Δt gerade. Berücksichtigen wir weiterhin, dass
- z(t) = x(t) + j · y(t) ist,
- x(t) und y(t) gleiche statistische Eigenschaften aufweisen, und
- es zwischen x(t) und y(t) keine statistischen Bindungen gibt,
so lässt sich für die AKF des komplexen Faktors z(t) schreiben:
\[\varphi_z ({\rm \Delta}t) = \varphi_x ({\rm \Delta}t) + \varphi_y ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t) \hspace{0.05cm}.\]
Daraus ergibt sich folgende Vereinfachung:
- Zur Ermittlung der statistischen Bindungen der komplexen Größe z(t) muss nur einer der beiden Gaußschen Zufallsprozesse betrachtet werden. Im Folgenden sei dies x(t).
- Wir berechnen zuerst die Autokorrelationsfunktion φx(Δt) = E[x(t) · x(t + Δt)] des Realteils und anschließend auch dessen Leistungsdichtespektrum (LDS)
- \[{\it \Phi}_x (f_{\rm D}) = \int_{-\infty}^{+\infty} \varphi_x ({\rm \Delta}t) \cdot {\rm exp} [ -{\rm j} \cdot 2 \pi \cdot f_{\rm D} \cdot {\rm \Delta}t] \hspace{0.15cm}{\rm d}({\rm \Delta}t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_x ({\rm \Delta}t) \hspace{0.05cm}.\]
- Für die entsprechenden Kenngrößen des komplexen Zufallsprozesses z(t) gilt dann:
- \[\varphi_z ({\rm \Delta}t) = 2 \cdot \varphi_x ({\rm \Delta}t)\hspace{0.05cm},\hspace{0.2cm} {\it \Phi}_z (f_{\rm D}) = 2 \cdot {\it \Phi}_x (f_{\rm D}) \hspace{0.05cm}.\]
Die LDS–Variable ist die Dopplerfrequenz fD, da beim Mobilfunk der Dopplereffekt die Ursache der statistischen Bindungen ist. Dieser Effekt wird auf der nächsten Seite erläutert.
Phänomenologische Beschreibung des Dopplereffektes
Die statistischen Bindungen innerhalb der reellen „Signale” x(t) und y(t) bzw. innerhalb der komplexen Größe z(t) sind auf den Dopplereffekt zurückzuführen. Dieser wurde Mitte des 19. Jahrhunderts von dem österreichischen Mathematiker, Physiker und Astronomen Christian Andreas Doppler theoretisch vorhergesagt und nach ihm benannt.
Qualitativ lässt sich der Dopplerreffekt wie folgt beschreiben:
- Nähern sich Beobachter und Quelle einander an, so erhöht sich aus Sicht des Beobachters die Frequenz, egal, ob sich der Beobachter bewegt oder die Quelle oder beide.
- Entfernt sich die Quelle vom Beobachter oder der Beobachter von der Quelle, so nimmt der Beobachter eine niedrigere Frequenz wahr, als tatsächlich gesendet wurde.
Den gleichen Effekt stellt man auch bei einem Autorennen fest. Die Frequenzänderungen und der „Sound” sind dabei um so deutlicher, je schneller die Autos fahren.
Den Sachverhalt kann man sich in diesem Lerntutorial mit dem Interaktionsmodul Dopplereffekt Please add file and don't upload flash videos. verdeutlichen. Einige Eigenschaften dieses noch aus dem Physikunterricht bekannten Effekts sollen nun anhand von Bildschirmabzügen aus dieser Flash–Animation dargestellt werden, wobei natürlich die dynamischen Programmeigenschaften verloren gehen.
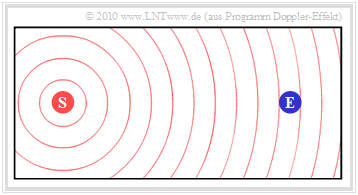
Die Grafik zeigt die Ausgangssituation. Der ruhende Sender (S) gibt eine konstante Frequenz fS ab. Die Wellenausbreitung ist in der Grafik durch konzentrische Kreise um (S) veranschaulicht. Beim ebenfalls ruhenden Empfänger (E) kommt dann natürlich die Frequenz fE = fS an.
Die phänomenologische Erklärung des Dopplereffektes wird auf der nächsten Seite fortgesetzt.
Phänomenologische Beschreibung des Dopplereffektes (2)
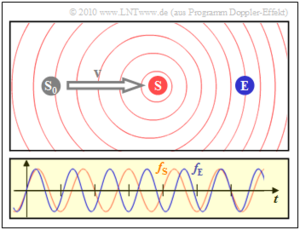
Der nächste Schnappschuss zeigt den Fall, dass sich der Sender (S) mit konstanter Geschwindigkeit υ von seinem Startpunkt S0 auf den Empfänger (E) zu bewegt hat.
Das Diagramm zeigt, dass die vom Empfänger wahrgenommene Frequenz fE (blaue Schwingung) um etwa 20% größer ist als die Frequenz fS am Sender (rote Schwingung). Aufgrund der Bewegung des Senders sind nun die Kreise nicht mehr konzentrisch.
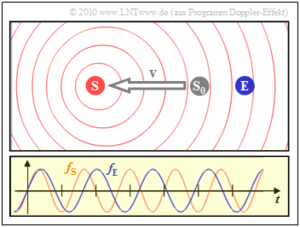
Die zweite Szenerie ergibt sich, wenn sich der Sender (S) vom Empfänger entfernt. Dann ist die Empfangsfrequenz fE (blaue Schwingung) um etwa 20% kleiner als die gesendete Frequenz fS.
Diese Angaben gelten für unrealistisch große Geschwindigkeit (υ = c/5). Beim Mobilfunk sind die Abweichungen zwischen fS und fE meist nur ein Bruchteil der Sendefrequenz.
Die exakte Gleichung für die Empfangsfrequenz fE unter Einbeziehung eines Winkels α zwischen der Bewegungsrichtung und der Verbindungslinie Sender–Empfänger lautet:
\[f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c \cdot \cos(\alpha)} \hspace{0.3cm}{\rm mit }\hspace{0.3cm} c = 3 \cdot 10^8 \, {\rm m/s} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\rm Lichtgeschwindigkeit} \hspace{0.05cm}.\]
Wie in Aufgabe Z1.4 gezeigt werden soll, kann man bei realistischen Geschwindigkeiten (υ << c) von der folgenden Näherung ausgehen, bei der die durch die Relativitätstheorie beschriebenen Effekte unberücksichtigt bleiben:
\[f_{\rm E} \approx f_{\rm S} \cdot \left [1 +{v}/{c} \cdot \cos(\alpha) \right ] \hspace{0.05cm}.\]
Wir weisen Sie noch auf das folgende Interaktionsmodul hin:
Zur Verdeutlichung des Dopplereffekts. Please add link and do not upload flash videos
Dopplerfrequenz und deren Verteilung (1)
Wir fassen die Aussagen der letzten Seite nochmals kurz zusammen, wobei wir von der zweiten, also der nichtrelativistischen Gleichung ausgehen:
- Bei einer Relativbewegung zwischen Sender (Quelle) und Empfänger (Beobachter) kommt es zu einer Frequenzverschiebung um die Dopplerfrequenz fD = fE – fS.
- Eine positive Dopplerfrequenz (fE > fS) ergibt sich dann, wenn sich Sender und Empfänger (relativ) aufeinander zu bewegen. Eine negative Dopplerfrequenz (fE < fS) bedeutet, dass sich Sender und Empfänger (direkt oder unter einem Winkel) voneinander entfernen.
- Die maximale Frequenzverschiebung tritt auf, wenn sich Sender und Empfänger direkt aufeinander zu bewegen (⇒ Winkel α = 0°). Dieser Maximalwert hängt in erster Näherung von der Sendefrequenz fS und der Geschwindigkeit υ ab (c ist die Lichtgeschwindigkeit):
- \[f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.\]
- Erfolgt die Relativbewegung unter einem beliebigen Winkel α zu der Verbindungslinie Sender–Empfänger, so entsteht eine Dopplerverschiebung um
- \[f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} - \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \le f_{\rm D} \le + \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{0.05cm}.\]
Unter der Annahme gleichwahrscheinlicher Bewegungsrichtungen (Gleichverteilung für den Winkel α im Bereich –π ≤ α ≤ +π) ergibt sich für die Wahrscheinlichkeitsdichtefunktion der Dopplerfrequenz im Bereich –fD, max ≤ fD ≤ +fD, max:
\[{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
Außerhalb des Bereichs |fD| > fD, max ist die Wahrscheinlichkeitsdichte identisch 0.
Herleitung: Die entstehende Dopplerfrequenz in Abhängigkeit des Bewegungswinkels α lautet:
\[f_{\rm D} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) = g(\alpha) \hspace{0.05cm}.\]
Wir bezeichnen diese Funktion mit g(α) und gehen davon aus, dass α alle Winkelwerte zwischen ±π mit gleicher Wahrscheinlichkeit annimmt. Dann ergibt sich für die Wahrscheinlichkeit der Dopplerfrequenz entsprechend dem Kapitel 3.7 im Buch „Stochastische Signaltheorie”
\[{\rm wdf}(f_{\rm D})=\frac{{\rm wdf}(\alpha)}{\mid g'(\alpha)\mid}\Bigg |_{\hspace{0.1cm} \alpha=h(f_{\rm D})} \hspace{0.05cm}\]
mit der Ableitung g'(α) = –fD, max · sin(α) und der Umkehrfunktion α = h(fD). Im betrachteten Beispiel lautet die Umkehrfunktion: α = arccos(fD/fD, max).
Die Herleitung wird auf der nächsten Seite fortgesetzt. Diese überspringen?
Dopplerfrequenz und deren Verteilung (2)
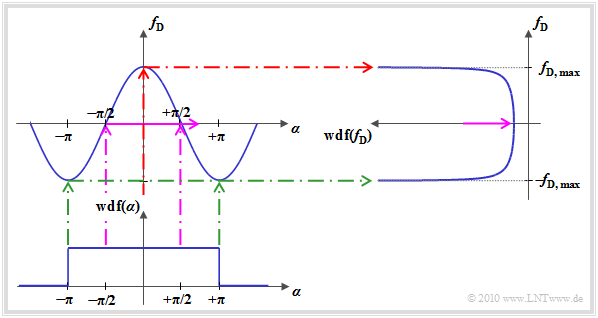
Die Grafik veranschaulicht den Rechengang zur Bestimmung der Dopplerfrequenz–WDF:
- Da die Kennlinie g(α) = fD, max · cos(α) zwischen der Dopplerfrequenz fD und dem Winkel α auf ±fD, max begrenzt ist, ist für fD kein Wert außerhalb dieses Bereichs möglich.
- Bei der Transformation von Zufallsgrößen muss zwischen Bereichen mit positiver und negativer Steigung der Transformationskennlinie unterschieden werden. Die α–Werte zwischen –π und 0 (positive Steigung der Transformationskennlinie) liefern das Ergebnis
- \[{\rm wdf}(f_{\rm D})\hspace{-0.1cm} = \hspace{-0.1cm}\frac{1/(2\pi)}{f_{\rm D, \hspace{0.05cm} max} \cdot \sin(\alpha)}\Bigg |_{\hspace{0.1cm} \alpha=\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})} = \frac{(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} )^{-1}}{ \sin(\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}))} = \]
- \[ \hspace{1.5cm} = \hspace{-0.1cm} \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- Aus Symmetriegründen trägt der positive α–Bereich in gleicher Weise bei, so dass im inneren Bereich insgesamt gilt:
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- Winkel im Bereich um α = ±π/2 führen zu einer kleinen Dopplerfrequenz ⇒ fD ≈ 0 (violette Markierung). Aufgrund der relativ großen Steigung der cosinusförmigen Kennlinie g(α) bei α = ±π/2 ist der WDF–Wert bei fD ≈ 0 allerdings sehr klein.
- Kleine Winkel (um α ≈ 0) führen dagegen zur maximalen Dopplerfrequenz ⇒ fD ≈ fD, max (rote Markierung). Aufgrund der nahezu horizontalen Kennlinie g(α) ist hier die fD–WDF deutlich größer. Für fD = fD, max ergibt sich sogar ein unendlich großer Wert.
- Winkel um α = ±π führen zur Dopplerfrequenz ⇒ fD ≈ –fD, max (grüne Markierung). Auch hier ist die Kennlinie nahezu horizontal und es ergibt sich wiederum ein großer WDF–Wert.
AKF und LDS bei Rayleigh–Fading
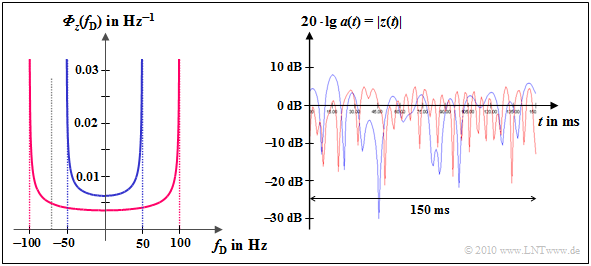
Wir setzen nun eine in alle Richtungen gleich abstrahlende Antenne voraus. Dann ist das Doppler–LDS formgleich mit der WDF der Dopplerfrequenzen. Für Φx(fD) muss die WDF noch mit der Leistung σ2 des Gaußprozesses multipliziert werden, und für das resultierende LDS Φz(fD) des komplexen Faktors z(t) = x(t) + j · y(t) gilt nach Verdoppelung:
\[{\it \Phi}_z(f_{\rm D}) = \left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} |f_{\rm D}| \le f_{\rm D, \hspace{0.05cm} max} \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.\]
Man bezeichnet diesen Verlauf nach W.C. Jakes als das Jakes–Spektrum. Die Verdoppelung ist notwendig, da wir bisher nur den Beitrag des Realteils x(t) betrachtet haben. Die Verdoppelung ist notwendig, da wir bisher nur den Beitrag des Realteils x(t) betrachtet haben.
Die zugehörige Autokorrelationsfunktion (AKF) erhält man nach Fourierrücktransformation:
\[\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm},\]
mit der Besselfunktion erster Art und nullter Ordnung (Definition und Reihenentwicklung):
\[{\rm J }_0 (u) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{- {\rm j }\hspace{0.03cm}\cdot \hspace{0.03cm}u \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} = \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(-1)^k \cdot (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
Besselfunktion erster Art und nullter Ordnung Please add link and do not upload flash videos (Interaktionsmodul)
Das rechte Bild zeigt den logarithmierten Betrag von z(t). Man erkennt das doppelt so schnelle Fading des roten Kurvenverlaufs. Die Rayleigh–WDF ist in beiden Fällen gleich.
Aufgaben
Zusatzaufgaben:1.4 Zum Dopplereffekt
A1.5 Nachbildung des Jakes–Spektrums