Aufgaben:Aufgabe 2.2: Modulationsgrad: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/ Zweiseitenband-Amplitudenmodulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Ch…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID989__Mod_A_2_2.png|right|]] |
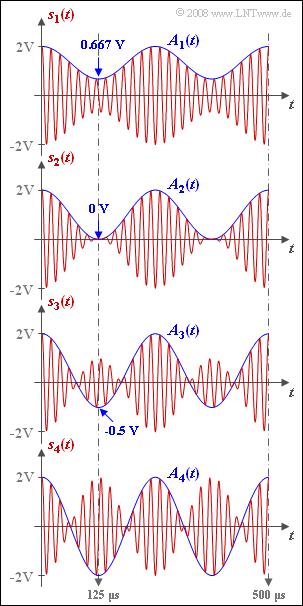
| + | Die Grafik zeigt ZSB–amplitudenmodulierte Signale $s_1(t)$ bis $s_4(t)$ mit unterschiedlichem Modulationsgrad. Das Nachrichtensignal $q(t)$ und das Trägersignal $z(t)$ seien jeweils cosinusförmig: | ||
| + | $$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$ | ||
| + | $$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | Das modulierte Signal (Sendesignal) lautet somit mit dem im Modulator zugesetzten Gleichanteil $A_T$: | ||
| + | $$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ | ||
| + | Ist der Modulationsgrad m ≤ 1, so ist A(t) gleich der Hüllkurve a(t). Dagegen gilt für m > 1: | ||
| + | $$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$ | ||
| + | Der cosinusförmige Verlauf $A(t)$ schwankt zwischen $A_{max}$ und $A_{min}$, wobei wegen der obigen Normierung stets $A_{max} = 2V$ ist. Die Minimalwerte von $A(t)$ treten zum Beispiel bei der halben Periodendauer des Quellensignals (also für $t = 125 μs$) auf: | ||
| + | $$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$ | ||
| + | Die Zahlenwerte sind in der Grafik angegeben. | ||
| + | '''Hinweis:'''Die Aufgabe bezieht sich auf den Theoriteil von [http://www.lntwww.de/Modulationsverfahren/Zweiseitenband-Amplitudenmodulation Kapitel 2.1]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 28. Dezember 2016, 13:55 Uhr
Die Grafik zeigt ZSB–amplitudenmodulierte Signale $s_1(t)$ bis $s_4(t)$ mit unterschiedlichem Modulationsgrad. Das Nachrichtensignal $q(t)$ und das Trägersignal $z(t)$ seien jeweils cosinusförmig: $$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$ $$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$ Das modulierte Signal (Sendesignal) lautet somit mit dem im Modulator zugesetzten Gleichanteil $A_T$: $$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ Ist der Modulationsgrad m ≤ 1, so ist A(t) gleich der Hüllkurve a(t). Dagegen gilt für m > 1: $$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$ Der cosinusförmige Verlauf $A(t)$ schwankt zwischen $A_{max}$ und $A_{min}$, wobei wegen der obigen Normierung stets $A_{max} = 2V$ ist. Die Minimalwerte von $A(t)$ treten zum Beispiel bei der halben Periodendauer des Quellensignals (also für $t = 125 μs$) auf: $$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$ Die Zahlenwerte sind in der Grafik angegeben.
Hinweis:Die Aufgabe bezieht sich auf den Theoriteil von Kapitel 2.1.
Fragebogen
Musterlösung