Aufgaben:Aufgabe 4.1: Zum „Log Likelihood Ratio”: Unterschied zwischen den Versionen
| Zeile 47: | Zeile 47: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie hängen die bedingten Wahrscheinlichkeiten zweier Zufallsgrößen $A$ und $B$ zusammen? |
|type="[]"} | |type="[]"} | ||
| − | + | - ${\rm Pr}(A | B) = {\rm Pr}(B | A)$, | |
| − | - | + | - ${\rm Pr}(A | B) = {\rm Pr}(B | A) \cdot {\rm Pr}(B) / {\rm Pr}(A)$, |
| + | + ${\rm Pr}(A \ | \ B) = {\rm Pr}(B \ | \ A) \cdot {\rm Pr}(A) \ / \ {\rm Pr}(B)$. | ||
| − | { | + | {Welche Gleichung gilt für den Binärkanal mit den Wahrscheinlichkeiten ${\rm Pr}(A) = {\rm Pr}(x = 0)$ und ${\rm Pr}(B) = {\rm Pr}(y = 0)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + ${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 \ | \ x = 0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)$, |
| − | |||
{Multiple-Choice | {Multiple-Choice | ||
Version vom 6. Dezember 2017, 09:41 Uhr
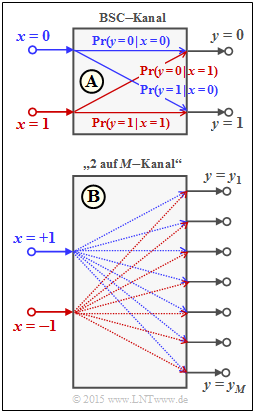
Zur Interpretation von Log–Likelihood–Verhältnissen (kurz $L$–Werten) gehen wir wie im Theorieteil vom Binary Symmetric Channel (BSC) aus. Die englische Bezeichung ist Log Likelihood Ratio (LLR).
Für die binären Zufallsgrößen am Eingang und Ausgang gelte
- $$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}. $$
Dieses Modell ist in der oberen Grafik dargestellt und wird im Folgenden als Modell A bezeichnet. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt:
- $${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$
- $${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$
Die Verfälschungswahrscheinlichkeit $\epsilon$ ist der entscheidende Parameter des BSC–Modells.
Bezüglich der Wahrscheinlichkeitsverteilung am Eingang ist es zweckmäßig, anstelle der Wahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ das Log Likelihood Ratio (LLR) zu betrachten.
Für dieses gilt bei der hier verwendeten unipolaren Betrachtungsweise per Definition:
- $$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$
wobei der Index „A” auf die Apriori–Wahrscheinlichkeit hinweist.
Beispielsweise ergibt sich für ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ das Apriori–LLR $L_{\rm A}(x) = \, –1.382$.
Aus dem BSC–Modell lässt sich zudem der $L$–Wert der bedingten Wahrscheinlichkeiten ${\rm Pr}(y|x)$ in Vorwärtsrichtung ermitteln, der in der vorliegenden Aufgabe auch mit $L_{\rm V}(y)$ bezeichnet wird:
- $$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.05cm} y = 0, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$
Beispielsweise ergibt sich für $\epsilon = 0.1$:
- $$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$
Von besonderer Bedeutung für die Codierungstheorie sind die Rückschlusswahrscheinlichkeiten ${\rm Pr}(x|y)$, die mit den Vorwärtswahrscheinlichkeiten ${\rm Pr}(y|x)$ sowie den Eingangswahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ über den Satz von Bayes in Zusammenhang stehen. Der entsprechende $L$–Wert wird in dieser Aufgabe mit $L_{\rm R}(y)$ bezeichnet:
- $$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$
Hinweise:
- Die Aufgabe bezieht sich auf die ersten Seiten des Kapitels Soft–in Soft–out Decoder.
- In den letzten Teilaufgaben ist zu klären, ob die gefundenen Zusammenhänge zwischen $L_{\rm A}, \ L_{\rm V}$ und $L_{\rm R}$ auch auf den unten skizzierten „2–auf–$M$–Kanal” übertragen werden können. Hierzu wählen wir für die Eingangssymbole eine bipolare Betrachtungsweise: „$0$” → „$+1$” sowie „$1$” → „$–1$”.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung