Aufgaben:Aufgabe 3.3Z: Optimierung eines Koaxialkabelsystems: Unterschied zwischen den Versionen

Version vom 24. Oktober 2017, 11:51 Uhr

Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen:

Die Sendeimpulse sind NRZ–rechteckförmig und besitzen die Energie $E_B = s_0^2 \cdot T$.
Der Kanal ist ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 40 \, {\rm dB}$.
Es liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0 = 0.0001 \cdot E_B$ vor.
Der Empfängerfrequenzgang $H_E(f)$ beinhaltet einen idealen Kanalentzerrer $H_K^{\rm -1}(f) und einen Gaußtiefpass $H_G(f)$ mit Grenzfrequenz $f_G$ zur Rauschleistungsbegrenzung. Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_D)$ sowie den Detektionsrauscheffektivwert \sigma_d – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_G$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit :'"`UNIQ-MathJax3-QINU`"' möglichst klein ist. Die ungünstigste Fehlerwahrscheinlichkeit stellt eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_S$ dar. Für $f_G \cdot T ≥ 0.4$ kann auch eine untere Schranke angegeben werden:

$${1}/{4} \cdot p_{\rm U}\le p_{\rm S}\le p_{\rm U} \hspace{0.05cm}.$$

Hinweis: Die Aufgabe gehört zum Themengebit von [[Digitalsignalübertragung/Berücksichtigung_von_Kanalverzerrungen_und_Entzerrung|Kapitel 3.3]. Zur numerischen Auswertung der Q–Funktion können Sie das folgende Interaktionsmodul nutzen: Gaußsche Fehlerfunktion

Fragebogen

Musterlösung

(1) (2) (3) (4) (5)

@@ Zeile 4: / Zeile 4: @@
 [[Datei:P_ID1409__Dig_Z_3_3.png|right|frame]]
+Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen:
+* Die Sendeimpulse sind NRZ&ndash;rechteckförmig und besitzen die Energie $E_B = s_0^2 \cdot T$.
+* Der Kanal ist ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 40 \, {\rm dB}$.
+* Es liegt AWGN&ndash;Rauschen mit der Rauschleistungsdichte $N_0 = 0.0001 \cdot E_B$ vor.
+* Der Empfängerfrequenzgang $H_E(f)$ beinhaltet einen idealen Kanalentzerrer $H_K^{\rm -1}(f) und einen Gaußtiefpass $H_G(f)$ mit Grenzfrequenz $f_G$ zur Rauschleistungsbegrenzung.
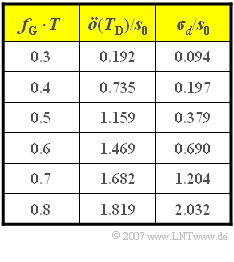
+Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_D)$ sowie den Detektionsrauscheffektivwert \sigma_d &ndash; jeweils normiert auf die Sendeamplitude $s_0$ &ndash; für verschiedene Grenzfrequenzen $f_G$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit
+:$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}
+  \right) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}}\right)$$
+möglichst klein ist. Die ungünstigste Fehlerwahrscheinlichkeit stellt eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_S$ dar. Für $f_G \cdot T &#8805; 0.4$ kann auch eine untere Schranke angegeben werden:
+:$${1}/{4} \cdot p_{\rm U}\le p_{\rm S}\le p_{\rm U}
+ \hspace{0.05cm}.$$
+''Hinweis:'' Die Aufgabe gehört zum Themengebit von [[Digitalsignal%C3%BCbertragung/Ber%C3%BCcksichtigung_von_Kanalverzerrungen_und_Entzerrung|Kapitel 3.3]. Zur numerischen Auswertung der Q&ndash;Funktion können Sie das folgende Interaktionsmodul nutzen:
+[https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=1706&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross|Komplementäre Gaußsche Fehlerfunktion]
 ===Fragebogen===

	correct
	false