Aufgaben:Aufgabe 1.2: Lognormal – Kanalmodell: Unterschied zwischen den Versionen

Version vom 20. Oktober 2017, 19:10 Uhr

Wir betrachten eine Mobilfunkzelle im städtischen Bereich und ein Fahrzeug, das sich näherungsweise in einem festen Abstand d₀ von der Basisstation aufhält. Beispielsweise bewegt es sich auf einem Kreisbogen um die Basisstation. Somit ist der gesamte Pfadverlust durch folgende Gleichung beschreibbar:

$$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$

V₀ berücksichtigt den entfernungsabhängigen Pfadverlust, der mit V₀ = 80 dB als konstant angenommen wird. Der Verlust V_S ist auf Abschattungen (Shadowing) zurückzuführen, der durch die Lognormal–Verteilung mit der Wahrscheinlichkeitsdichtefunktion

$$f_{V{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}- m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$

ausreichend genau beschrieben wird (siehe Grafik). Es gelten folgende Zahlenwerte:

$$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.15cm}{\rm bzw.}\hspace{0.15cm}\sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm (Teilaufgabe\hspace{0.15cm} b)}\hspace{0.05cm}.$$

Gehen Sie außerdem von folgenden einfachen Annahmen aus:

Die Sendeleistung beträgt P_S = 10 W (oder 40 dBm).
Die Empfangsleistung soll mindestens P_E = 10 pW (umgerechnet: –80 dBm) betragen.

Hinweis: Die Aufgabe gehört zum Kapitel 1.1. Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden:

$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$

Oder Sie benutzen das von LNTwww bereitgestellte Flash–Modul.

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 4: / Zeile 4: @@
 [[Datei:P_ID2122__Mob_A_1_2.png|right|frame]]
+Wir betrachten eine Mobilfunkzelle im städtischen Bereich und ein Fahrzeug, das sich näherungsweise in einem festen Abstand <i>d</i><sub>0</sub> von der Basisstation aufhält. Beispielsweise bewegt es sich auf einem Kreisbogen um die Basisstation. Somit ist der gesamte Pfadverlust durch folgende Gleichung beschreibbar:
+:$$V_{\rm P} =  V_{\rm 0} + V_{\rm S}  \hspace{0.05cm}.$$
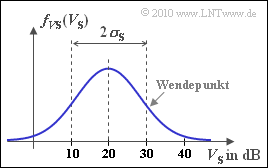
+<i>V</i><sub>0</sub> berücksichtigt den entfernungsabhängigen Pfadverlust, der mit <i>V</i><sub>0</sub> = 80 dB als konstant angenommen wird. Der Verlust <i>V</i><sub>S</sub> ist auf Abschattungen (<i>Shadowing</i>) zurückzuführen, der durch die Lognormal&ndash;Verteilung mit der Wahrscheinlichkeitsdichtefunktion
+:$$f_{V{\rm S}}(V_{\rm S}) =  \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}}  \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}-  m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$
+ausreichend genau beschrieben wird (siehe Grafik). Es gelten folgende Zahlenwerte:
+:$$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}  \sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.15cm}{\rm bzw.}\hspace{0.15cm}\sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm (Teilaufgabe\hspace{0.15cm} b)}\hspace{0.05cm}.$$
+Gehen Sie außerdem von folgenden einfachen Annahmen aus:
+* Die Sendeleistung beträgt <i>P</i><sub>S</sub> = 10 W (oder 40 dBm).
+* Die Empfangsleistung soll mindestens <i>P</i><sub>E</sub> = 10 pW  (umgerechnet: &ndash;80 dBm) betragen.
+''Hinweis:'' Die Aufgabe gehört zum [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Kapitel 1.1]].
+Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden:
+:$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm}
+ {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$
+Oder Sie benutzen das von LNTwww bereitgestellte Flash&ndash;Modul.

	Falsch
	Richtig